
科目: 来源: 题型:
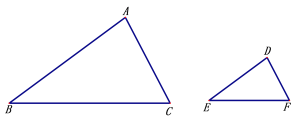
【题目】求证:相似三角形对应角的角平分线之比等于相似比.要求:
①分别在给出的△ABC与△DEF中用尺规作出一组对应角的平分线,不写作法,保留作图痕迹;
②在完成作图的基础上,写出已知、求证,并加以证明.
查看答案和解析>>
科目: 来源: 题型:
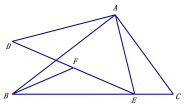
【题目】如图,△ABC∽△ADE,∠BAC =∠ADE =90°,AB=4,AC=3,F是DE的中点,若点E是直线BC上的动点,连接BF,则BF的最小值是_______.
查看答案和解析>>
科目: 来源: 题型:
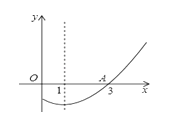
【题目】如图,抛物线![]() 的对称轴为直线x=1,与x轴的一个交点坐标为A(3,0),其部分图象如图所示,下列结论中: ①
的对称轴为直线x=1,与x轴的一个交点坐标为A(3,0),其部分图象如图所示,下列结论中: ①![]() ; ②方程
; ②方程![]() 的两个根是
的两个根是![]() ; ③
; ③![]() ;④
;④![]() ; ⑤当0<x<3时,y随x增大而减小;其中结论正确的个数是( )
; ⑤当0<x<3时,y随x增大而减小;其中结论正确的个数是( )
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目: 来源: 题型:
【题目】据海峡导报报道,为推进漳州绿色农业发展, 2018-2020年,漳州市将完成农业绿色发展项目总投资414亿元。已知漳州2018年已完成项目投资100亿元,假设后两年该项目投资的平均增长率为x,依题意可列方程为( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,一幢楼房AB背后有一台阶CD,台阶每层高0.2米,且AC=14.5米,NF=0.2米.设太阳光线与水平地面的夹角为α,当α=56.3°时,测得楼房在地面上的影长AE=10米,现有一只小猫睡在台阶的NF这层上晒太阳.

(1)求楼房的高度约为多少米?
(2)过了一会儿,当α=45°时,问小猫能否还晒到太阳?请说明理由.(参考数据:sin56.3°≈0.83,cos56.3°≈0.55,tan56.3°≈1.5)
查看答案和解析>>
科目: 来源: 题型:
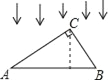
【题目】如图,在Rt△ABC中,∠C=90°,投影线方向如图所示,点C在斜边AB上的正投影为点D,
(1)试写出边AC、BC在AB上的投影;
(2)试探究线段AC、AB和AD之间的关系;
(3)线段BC、AB和BD之间也有类似的关系吗?请直接写出结论.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,小明家窗外有一堵围墙AB,由于围墙的遮挡,清晨太阳光恰好从窗户的最高点C射进房间的地板F处,中午太阳光恰好能从窗户的最低点D射进房间的地板E处,小明测得窗子距地面的高度OD=0.8 m,窗高CD=1.2 m,并测得OE=0.8 m,OF=3 m,求围墙AB的高度.

查看答案和解析>>
科目: 来源: 题型:
【题目】一块材料的形状是锐角三角形ABC,边BC=12cm,高AD=8cm,把它加工成矩形零件如图,要使矩形的一边在BC上,其余两个顶点分别在AB,AC上.且矩形的长与宽的比为3:2,求这个矩形零件的边长.

查看答案和解析>>
科目: 来源: 题型:
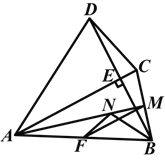
【题目】(2014山东淄博)如图,四边形ABCD中,AC⊥BD交BD于点E,点F,M分别是AB,BC的中点,BN平分∠ABE交AM于点N,AB=AC=BD,连接MF,NF.
(1)判断△BMN的形状,并证明你的结论;
(2)判断△MFN与△BDC之间的关系,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在锐角三角形ABC中,点D,E分别在边AC,AB上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC.
(1)求证:△ADE∽△ABC;
(2)若AD=3,AB=5,求![]() 的值.
的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com