
科目: 来源: 题型:
【题目】如图1,抛物线y=﹣x2+mx+n交x轴于点A(﹣2,0)和点B,交y轴于点C(0,2).
(1)求抛物线的函数表达式;
(2)若点M在抛物线上,且S△AOM=2S△BOC,求点M的坐标;
(3)如图2,设点N是线段AC上的一动点,作DN⊥x轴,交抛物线于点D,求线段DN长度的最大值.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,AB为⊙O直径,C是⊙O上一点,CO⊥AB于点O,弦CD与AB交于点F,过点D作∠CDE=∠DFE,DE交AB的延长线于点E,过点A作⊙O的切线交ED的延长线于点G.
(1)求证:GE是⊙O的切线;
(2)若tanC=![]() ,BE=4,求AG的长.
,BE=4,求AG的长.

查看答案和解析>>
科目: 来源: 题型:
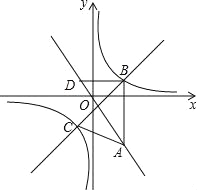
【题目】如图,在平面直角坐标系xOy中,点A(a,﹣![]() )在直线y=﹣
)在直线y=﹣![]() 上,AB∥y轴,且点B的纵坐标为1,双曲线y=
上,AB∥y轴,且点B的纵坐标为1,双曲线y=![]() 经过点B.
经过点B.
(1)求a的值及双曲线y=![]() 的解析式;
的解析式;
(2)经过点B的直线与双曲线y=![]() 的另一个交点为点C,且△ABC的面积为
的另一个交点为点C,且△ABC的面积为![]() .
.
①求直线BC的解析式;
②过点B作BD∥x轴交直线y=﹣![]() 于点D,点P是直线BC上的一个动点.若将△BDP以它的一边为对称轴进行翻折,翻折前后的两个三角形所组成的四边形为正方形,直接写出所有满足条件的点P的坐标.
于点D,点P是直线BC上的一个动点.若将△BDP以它的一边为对称轴进行翻折,翻折前后的两个三角形所组成的四边形为正方形,直接写出所有满足条件的点P的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】作图并填空
如图,在Rt△ABC,∠BAC=90°,AD⊥BC于D,在②③图中,MN=AB,∠MNE=∠B,现要以②③图为基础,在射线NE上确定一点P,构造出一个△MNP与①图中某一个三角形全等.
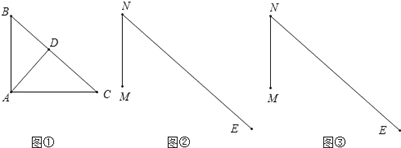
(1)用边长限制P点,画法:_____,可根据SAS,AAS,ASA,HL中的______得到______.
(2)用直角限制点P,画法:_______,可根据SAS,AAS,ASA,HL中的______得到______.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,正方形ABCD中,AB=4cm,点E、F同时从C点出发,以1cm/s的速度分别沿CB﹣BA、CD﹣DA运动,到点A时停止运动.设运动时间为t(s),△AEF的面积为S(cm2),则S(cm2)与t(s)的函数关系可用图象表示为( )
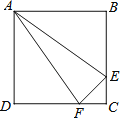
A. 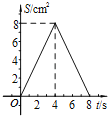 B.
B. 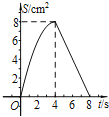
C. 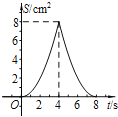 D.
D. 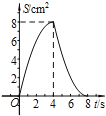
查看答案和解析>>
科目: 来源: 题型:
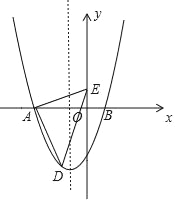
【题目】如图,在平面直角坐标系中,二次函数y=ax2+bx﹣3交x轴于点A(﹣3,0)、B(1,0),在y轴上有一点E(0,1),连接AE.
(1)求二次函数的表达式;
(2)若点D为抛物线在x轴负半轴下方的一个动点,求△ADE面积的最大值;
(3)抛物线对称轴上是否存在点P,使△AEP为等腰三角形?若存在,请直接写出所有P点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,O为菱形ABCD对角线上一点,以点O为圆心,OA长为半径的⊙O与BC相切于点M.
(1)求证:CD与⊙O相切;
(2)若菱形ABCD的边长为2,∠ABC=60°,求⊙O的半径.

查看答案和解析>>
科目: 来源: 题型:
【题目】凤城商场经销一种高档水果,售价为每千克50元
(1)连续两次降价后售价为每千克32元,若每次下降的百分率相同.求平均下降的百分率;
(2)已知这种水果的进价为每千克40元,每天可售出500千克,经市场调查发现,若每千克涨价1元,日销售量将减少20千克,每千克应涨价多少元才能使每天获得的利润最大?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,点D、E分别在AB、AC上,且CE=BC,连接CD,将线段CD绕点C按顺时针方向旋转90°后得到CF,连接EF.
(1)求证:△BDC≌△EFC;
(2)若EF∥CD,求证:∠BDC=90°.

查看答案和解析>>
科目: 来源: 题型:
【题目】凤城中学九年级(3)班的班主任让同学们为班会活动设计一个摸球方案,这些球除颜色外都相同,拟使中奖概率为50%.
(1)小明的设计方案:在一个不透明的盒子中,放入黄、白两种颜色的球共6个,搅匀后从中任意摸出1个球,摸到黄球则表示中奖,否则不中奖.如果小明的设计符合老师要求,则盒子中黄球应有 个,白球应有 个;
(2)小兵的设计方案:在一个不透明的盒子中,放入2个黄球和1个白球,搅匀后从中任意摸出2个球,摸到的2个球都是黄球则表示中奖,否则不中奖,该设计方案是否符合老师的要求?试说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com