A. 不公平，小刚、小华占便宜了 B. 公平 C. 不公平，小华吃亏了 D. 不公平，小华占便宜了

【题目】如图，在同一平面内，将两个全等的等腰直角和摆放在一起，为公共顶点，，它们的斜边长为2，若固定不动，绕点旋转，、与边的交点分别为、(点不与点重合，点不与点重合)，设，.

(1)请在图中找出两对相似而不全等的三角形，并选取其中一对加以证明.

(2)求与的函数关系式，直接写出自变量的取值范围.

【题目】如图，关于的二次函数的图像与轴交于点和点，与轴交于点，抛物线的对称轴与轴交于点.

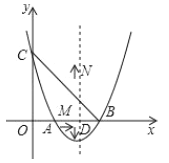
(1)求二次函数的表达式；

(2)在轴上是否存在一点，使为等腰三角形？若存在，请求出点的坐标；

(3)有一个点从点出发，以每秒1个单位的速度在上向点运动，另一个点从点与点同时出发，以每秒2个单位的速度在抛物线的对称轴上运动，当点到达点时，点、同时停止运动，问点、运动到何处时，面积最大，试求出最大面积.

【题目】如图，O为坐标原点，点A(1，5)和点B(m，1)均在反比例函数y＝图象上．

(1)求m，k的值；

(2)设直线AB与x轴交于点C，求△AOC的面积．

【题目】如图：是的直径，是弦，，延长到点，使得.

(1)求证：是的切线；

(2)若，求的长.

【题目】如图，抛物线与x轴交于A、B两点，与y轴交于点C(0，3)

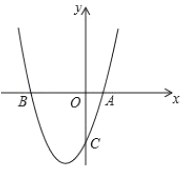
(1)求该抛物线的解析式；

(2)点为该抛物线上的一点、且在第二象限内，连接，若，求点的坐标；

(3)若点为线段上一动点，试求的最小值.

【题目】如图，抛物线与x轴交于点A（，0）、点B（2，0），与y轴交于点C（0，1），连接BC．

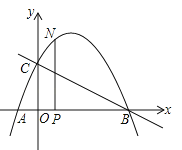
（1）求抛物线的函数关系式；

（2）点N为抛物线上的一个动点，过点N作NP⊥x轴于点P，设点N的横坐标为t（），求△ABN的面积S与t的函数关系式；

（3）若且时△OPN∽△COB，求点N的坐标．

(2)将（1）中的正方形ABCD变为矩形ABCD，等腰Rt△AEF变为Rt△AEF，且AD＝kAB,AF＝kAE,其他条件不变.(1)中的结论是否发生变化？结合图(2)说明理由；

(3)将（2）中的矩形ABCD变为平行四边形ABCD，将Rt△AEF变为△AEF，且∠BAD＝∠EAF＝，其他条件不变.(2)中的结论是否发生变化？结合图(3)，如果不变，直接写出结论；如果变化，直接用k表示出线段BE、DF的数量关系，用表示出直线BE、DF形成的锐角.

(1)求抛物线的解析式及顶点坐标；

(2)在轴上是否存在一点C，与A，B组成等腰三角形？若存在，求出点C的坐标，若不存在，请说明理由；

(3)在直线AB的下方抛物线上找一点P，连接PA，PB使得△PAB的面积最大，并求出这个最大值.

【题目】如图，点A，B，C都在抛物线y=ax2﹣2amx+am2+2m﹣5（其中﹣＜a＜0）上，AB∥x轴，∠ABC=135°，且AB=4．

（1）填空：抛物线的顶点坐标为 （用含m的代数式表示）；

（2）求△ABC的面积（用含a的代数式表示）；

（3）若△ABC的面积为2，当2m﹣5≤x≤2m﹣2时，y的最大值为2，求m的值．