
科目: 来源: 题型:
【题目】如图,在△ABC中,BD、CE是角平分线,AM⊥BD于点M,AN⊥CE于点N.△ABC的周长为30,BC=12.则MN的长是( )
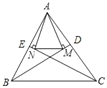
A. 15B. 9C. 6D. 3
查看答案和解析>>
科目: 来源: 题型:
【题目】下表记录了一名球员在罚球线上投篮的结果,这么球员投篮一次,投中的概率约是( )
投篮次数 | 10 | 50 | 100 | 150 | 200 | 250 | 300 | 500 |
投中次数 | 4 | 35 | 60 | 78 | 104 | 123 | 152 | 251 |
投中频率 | 0.40 | 0.70 | 0.60 | 0.52 | 0.52 | 0.49 | 0.51 | 0.50 |
A. 0.7B. 0.6C. 0.5D. 0.4
查看答案和解析>>
科目: 来源: 题型:
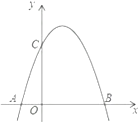
【题目】如图,是将抛物线y=-x2 平移后得到的抛物线,其对称轴为x=1,与x轴的一个交点为A(-1,0) ,另一交点为B,与y轴交点为C.
(1)求抛物线的函数表达式;
(2)若点N 为抛物线上一点,且BC⊥NC,求点N的坐标;
(3)点P是抛物线上一点,点Q是一次函数y=![]() x+
x+![]() 的图象上一点,若四边形OAPQ为平行四边形,这样的点P、Q是否存在?若存在,分别求出点P、Q的坐标,若不存在,说明理由.
的图象上一点,若四边形OAPQ为平行四边形,这样的点P、Q是否存在?若存在,分别求出点P、Q的坐标,若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】从三角形![]() 不是等腰三角形
不是等腰三角形![]() 一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.
一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.
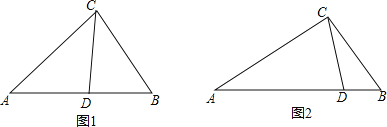
![]() 如图1,在
如图1,在![]() 中,CD为角平分线,
中,CD为角平分线,![]() ,
,![]() ,求证:CD为
,求证:CD为![]() 的完美分割线.
的完美分割线.
![]() 在
在![]() 中,
中,![]() ,CD是
,CD是![]() 的完美分割线,且
的完美分割线,且![]() 为等腰三角形,求
为等腰三角形,求![]() 的度数.
的度数.
![]() 如图2,
如图2,![]() 中,
中,![]() ,
,![]() ,CD是
,CD是![]() 的完美分割线,且
的完美分割线,且![]() 是以CD为底边的等腰三角形,求完美分割线CD的长.
是以CD为底边的等腰三角形,求完美分割线CD的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】边长为6的等边△ABC中,点D、E分别在AC、BC边上,DE∥AB,EC=2![]() .
.
(1)如图1,将△DEC沿射线EC方向平移,得到△D′E′C′,边D′E′与AC的交点为M,边C′D′与∠ACC′的角平分线交于点N,当CC′多大时,四边形MCND′为菱形?并说明理由.
(2)如图2,将△DEC绕点C旋转∠α(0°<α<360°),得到△D′E′C,连接AD′、BE′.边D′E′的中点为P.
①在旋转过程中,AD′和BE′有怎样的数量关系?并说明理由;
②连接AP,当AP最大时,求AD′的值.(结果保留根号)
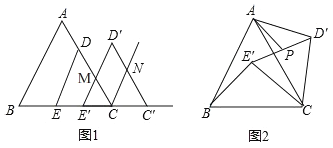
查看答案和解析>>
科目: 来源: 题型:
【题目】怡然美食店的A、B两种菜品,每份成本均为14元,售价分别为20元、18元,这两种菜品每天的营业额共为1120元,总利润为280元.
(1)该店每天卖出这两种菜品共多少份?
(2)该店为了增加利润,准备降低A种菜品的售价,同时提高B种菜品的售价,售卖时发现,A种菜品售价每降0.5元可多卖1份;B种菜品售价每提高0.5元就少卖1份,如果这两种菜品每天销售总份数不变,那么这两种菜品一天的总利润最多是多少?
查看答案和解析>>
科目: 来源: 题型:
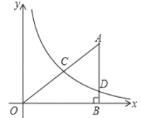
【题目】如图,在平面直角坐标系中,O为坐标原点,△ABO的边AB垂直与x轴,垂足为点B,反比例函数![]() (x>0)的图象经过AO的中点C,且与AB相交于点D,OB=4,AB=3.
(x>0)的图象经过AO的中点C,且与AB相交于点D,OB=4,AB=3.
(1)求反比例函数![]() 的解析式;
的解析式;
(2)设经过C,D两点的一次函数解析式为y1=k1x+b,求出其解析式,并根据图象直接写出在第一象限内,当y1>y时,x的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】太阳能光伏发电因其清洁、安全、便利、高效等特点,已成为世界各国普遍关注和重点发展的新兴产业,如图是太阳能电池板支撑架的截面图,其中的粗线表示支撑角钢,太阳能电池板与支撑角钢AB的长度相同,均为300cm,AB的倾斜角为![]() ,BE=CA=50cm,支撑角钢CD,EF与底座地基台面接触点分别为D,F,CD垂直于地面,
,BE=CA=50cm,支撑角钢CD,EF与底座地基台面接触点分别为D,F,CD垂直于地面,![]() 于点E.两个底座地基高度相同(即点D,F到地面的垂直距离相同),均为30cm,点A到地面的垂直距离为50cm,求支撑角钢CD和EF的长度各是多少cm(结果保留根号)
于点E.两个底座地基高度相同(即点D,F到地面的垂直距离相同),均为30cm,点A到地面的垂直距离为50cm,求支撑角钢CD和EF的长度各是多少cm(结果保留根号)


查看答案和解析>>
科目: 来源: 题型:
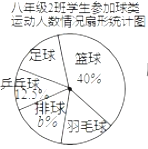
【题目】某校要求八年级同学在课外活动中,必须在五项球类(篮球、足球、排球、羽毛球、乒乓球)活动中任选一项(只能选一项)参加训练,为了了解八年级学生参加球类活动的整体情况,现以八年级2班作为样本,对该班学生参加球类活动的情况进行统计,并绘制了如图所示的不完整统计表和扇形统计图:

根据图中提供的信息,解答下列问题:
(1)a= ,b= ;
(2)该校八年级学生共有600人,则该年级参加足球活动的人数约 人;
(3)该班参加乒乓球活动的5位同学中,有3位男同学(A,B,C)和2位女同学(D,E),现准备从中选取两名同学组成双打组合,用树状图或列表法求恰好选出一男一女组成混合双打组合的概率.
查看答案和解析>>
科目: 来源: 题型:
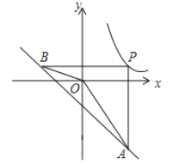
【题目】如图,P为反比例函数![]() (k>0)在第一象限内图象上的一点,过点P分别作x轴,y轴的垂线交一次函数y=﹣x﹣2的图象于点A、B.若∠AOB=135°,则k的值是________.
(k>0)在第一象限内图象上的一点,过点P分别作x轴,y轴的垂线交一次函数y=﹣x﹣2的图象于点A、B.若∠AOB=135°,则k的值是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com