
科目: 来源: 题型:
【题目】如图,以等边三角形ABC的BC边为直径画半圆,分别交AB、AC于点E、D,DF是圆的切线,过点F作BC的垂线交BC于点G.若AF的长为2,则FG的长为

A. 4 B. ![]() C. 6 D.
C. 6 D. ![]()
查看答案和解析>>
科目: 来源: 题型:
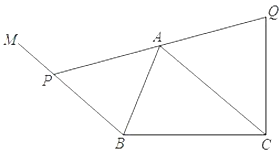
【题目】已知:如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() .过点
.过点![]() 作
作![]() ,动点
,动点![]() 在射线
在射线![]() 上(点
上(点![]() 不与
不与![]() 重合),联结
重合),联结![]() 并延长到点
并延长到点![]() ,使
,使![]() .
.
(1)求![]() 的面积;
的面积;
(2)设![]() ,
,![]() ,求
,求![]() 关于
关于![]() 的函数解析式,并写出
的函数解析式,并写出![]() 的取值范围;
的取值范围;
(3)连接![]() ,如果
,如果![]() 是直角三角形,求
是直角三角形,求![]() 的长.
的长.
查看答案和解析>>
科目: 来源: 题型:
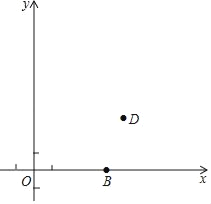
【题目】在平面直角坐标系![]() 中(如图),已知抛物线
中(如图),已知抛物线![]() 的图象经过点
的图象经过点![]() 、
、![]() ,设它与
,设它与![]() 轴的另一个交点为
轴的另一个交点为![]() (点
(点![]() 在点
在点![]() 的左侧),且
的左侧),且![]() 的面积是3.
的面积是3.
(1)求该抛物线的表达式;
(2)求![]() 的正切值;
的正切值;
(3)若抛物线与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() ,点
,点![]() 在射线
在射线![]() 上,当
上,当![]() 与
与![]() 相似时,求点
相似时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目: 来源: 题型:
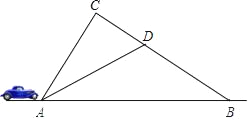
【题目】2018年首届“进博会”期间,上海对周边道路进行限速行驶.道路![]() 段为监测区,
段为监测区,![]() 、
、![]() 为监测点(如图).已知,
为监测点(如图).已知,![]() 、
、![]() 、
、![]() 在同一条直线上,且
在同一条直线上,且![]() ,
,![]() 米,
米,![]() ,
,![]() .
.
(1)求道路![]() 段的长;(精确到1米)
段的长;(精确到1米)
(2)如果![]() 段限速为60千米/时,一辆车通过
段限速为60千米/时,一辆车通过![]() 段的时间为90秒,请判断该车是否超速,并说明理由.(参考数据:
段的时间为90秒,请判断该车是否超速,并说明理由.(参考数据:![]()
![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图,反比例函数的图象经过点A、P,点A(6,![]() ),点P的横坐标是2.抛物线y=ax2+bx+c(a≠0)经过坐标原点,且与x轴交于点B,顶点为P.
),点P的横坐标是2.抛物线y=ax2+bx+c(a≠0)经过坐标原点,且与x轴交于点B,顶点为P.
求:(1)反比例函数的解析式;
(2)抛物线的表达式及B点坐标.

查看答案和解析>>
科目: 来源: 题型:
【题目】下列说法不正确的是( )
A. 设![]() 为单位向量,那么
为单位向量,那么![]()
B. 已知![]() 、
、![]() 、
、![]() 都是非零向量,如果
都是非零向量,如果![]() ,
,![]() ,那么
,那么![]()
C. 四边形![]() 中,如果满足
中,如果满足![]() ,
,![]() ,那么这个四边形一定是平行四边形
,那么这个四边形一定是平行四边形
D. 平面内任意一个非零向量都可以在给定的两个不平行向量的方向上分解
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线y=﹣x2+2x+3与x轴相交于A、B两点(点A在点B的左侧),与y轴相交于点C,顶点为D.
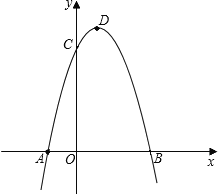
(1)直接写出A、B、C三点的坐标和抛物线的对称轴;
(2)连接BC,与抛物线的对称轴交于点E,点P为线段BC上的一个动点,过点P作PF∥DE交抛物线于点F,设点P的横坐标为m;
①用含m的代数式表示线段PF的长,并求出当m为何值时,四边形PEDF为平行四边形?
②设△BCF的面积为S,求S与m的函数关系式.
查看答案和解析>>
科目: 来源: 题型:
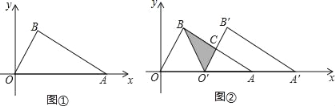
【题目】在平面直角坐标系中,点A(4,0),B为第一象限内一点,且OB⊥AB,OB=2.
(1)如图①,求点B的坐标;
(2)如图②,将△OAB沿x轴向右平移得到△O′A′B′,设OO′=m,其中0<m<4,连接BO′,AB与O′B′交于点C.
①试用含m的式子表示△BCO′的面积S,并求出S的最大值;
②当△BCO′为等腰三角形时,求点C的坐标(直接写出结果即可).
查看答案和解析>>
科目: 来源: 题型:
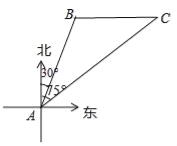
【题目】南海是我国的南大门,如图所示,某天我国一艘海监执法船在南海海域正在进行常态化巡航,在A处测得北偏东30°方向上,距离为20海里的B处有一艘不明身份的船只正在向正东方向航行,便迅速沿北偏东75°的方向前往监视巡查,经过一段时间后,在C处成功拦截不明船只,问我海监执法船在前往监视巡查的过程中行驶了多少海里(最后结果保留整数)?
![]()
![]() (参考数据:cos75°=0.2588,sin75°=0.9659,tan75°=3.732,
(参考数据:cos75°=0.2588,sin75°=0.9659,tan75°=3.732,![]() =1.732,
=1.732,![]() =1.414)
=1.414)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,AB为半圆O的直径,D为BA的延长线上一点,DC为半圆O的切线,切点为C.
(1)求证:∠ACD=∠B;
(2)如图2,∠BDC的平分线分别交AC,BC于点E,F;
①求tan∠CFE的值;
②若AC=3,BC=4,求CE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com