【题目】如图，直线相交于，在直线上分别取点,使，分别过点A，B作直线的垂线，垂足分别为，直线与交于，设．

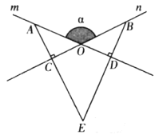
（1）求证：；

（2）小明说，不论是锐角还是钝角，点都在的平分线上，你认为他说的有道理吗？并说明理由．

（3）连接，当与三角板的形状相同时，直接写出的值．

【题目】小丽从学校去图书馆，小红沿同一条路从图书馆回学校，她们同时出发，小丽开始跑步中途改为步行，到达图书馆恰好用30分钟，小红骑自行车回学校，两人离学校的路程与各自离开出发地的时间（分钟）之间的函数图象如图所示．

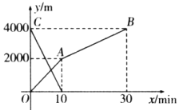
（1）小红骑自行车的速度是_____米/分钟，小丽从学校到图书馆的平均速度是_____米/分钟；

（2）求小丽从学校去图书馆时，与之间的函数关系式；

（3）两人出发后多少分钟相遇，相遇地点离图书馆的路程是多少米．(结果保留一位小数）．

【题目】如图，在直角坐标系的坐标轴上按如下规律取点：在轴正半轴上，在轴正半轴上，在轴负半轴上，在轴负半轴上，在轴正半轴上，......，且......，设......,有坐标分别为，......，．

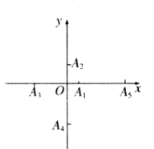
（1）当时，求的值；

（2）若，求的值；

（3）当时，直接写出用含为正整数)的式子表示轴负半轴上所取点．

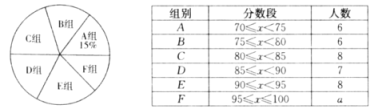
（1）统计表中，=_____；各组人数的中位数是_____；统计图中，组所在扇形的圆心角是_____°；

（2）李明同学得了88分，他说自己在参加选拔赛的同学中属于中午偏上水平，你认为他说的有道理吗？为什么？

（3）选出的10名优胜者中，男生、女生的分布情况如下表．

若从中任选1名男生和1名女生代表学校参加全区的比赛，请有列表法或画树状图法求男生和女生都出在四班的概率．

【题目】能够成为直角三角形三边长的三个正整数称为勾股数，世界上第一次给出勾股数公式的是我国古代数学著作《九章算术》，共勾股数的公式为：，其中是互质的奇数．

（1）当时，求这个三角形的面积；

（2）当时，计算三角形的周长（用含的代数式表示），并直接写出符合条件的三角形的周长值．

【题目】将一段抛物线向右依次平移3个单位，得到第2，3，4段抛物线，设这四段抛物线分别为，若直线与第四段抛物线有唯一公共点，则的取值范围是（　 ）

A.B.C.或D.

【题目】如图，正六边形和正五边形的边重合，的延长线与交于点，则的度数是（　　 ）

A.141B.144C.147D.150

【题目】如图，只改变正方形的形状，得到四边形，且，则四边形与正方形的面积的比是（ 　）

A.1:1B.2:3C.:2D.3:4

【题目】如图，抛物线与轴交于，两点，其中，，与轴交于点，抛物线的对称轴交轴于点，直线经过点，，连接．

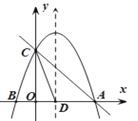
（1）求抛物线和直线的解析式：

（2）若抛物线上存在一点，使的面积是面积的2倍，求点的坐标；

（3）在抛物线的对称轴上是否存在一点，使线段绕点顺时针旋转得到线段，且恰好落在抛物线上？若存在，求出点的坐标；若不存在，请说叫理由．

【题目】已知，中，，，点为边中点，连接，点为的中点，线段绕点顺时针旋转得到线段，连接，．

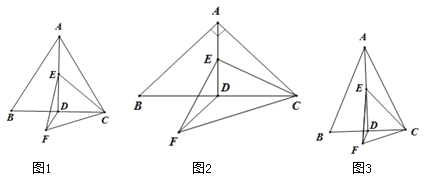
（1）如图1，当时，请直接写出的值；

（2）如图2，当时，（1）中的结论是否仍然成立？若成立，请给出证明；若不成立，请写出正确的结论，并说明理由；

（3）如图3，当时，请直接写出的值(用含的三角函数表示)．