
科目: 来源: 题型:
【题目】在平面直角坐标系中,分别过点![]() ,
,![]() 作
作![]() 轴的垂线
轴的垂线![]() 和
和![]() ,探究直线
,探究直线![]() 和
和![]() 与双曲线
与双曲线 ![]() 的关系,下列结论中错误的是
的关系,下列结论中错误的是
A.两直线中总有一条与双曲线相交
B.当![]() =1时,两条直线与双曲线的交点到原点的距离相等
=1时,两条直线与双曲线的交点到原点的距离相等
C.当![]() 时,两条直线与双曲线的交点在
时,两条直线与双曲线的交点在![]() 轴两侧
轴两侧
D.当两直线与双曲线都有交点时,这两交点的最短距离是2
查看答案和解析>>
科目: 来源: 题型:
【题目】□ABCD中,E、F是对角线BD上不同的两点,下列条件中,不能得出四边形AECF一定为平行四边形的是( )
A. BE=DF B. AE=CF C. AF//CE D. ∠BAE=∠DCF
查看答案和解析>>
科目: 来源: 题型:
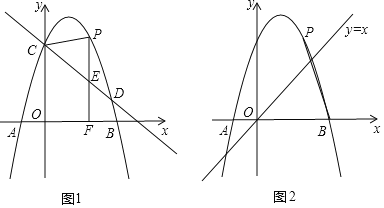
【题目】如图1所示,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 经过点
经过点![]() ,与抛物线另一个交点为
,与抛物线另一个交点为![]() ,点
,点![]() 是抛物线上的一个动点,过
是抛物线上的一个动点,过![]() 点作
点作![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]()
(1)求抛物线的解析式
(2)当点![]() 在直线
在直线![]() 上方,且
上方,且![]() 是以
是以![]() 为腰的等腰三角形时,求
为腰的等腰三角形时,求![]() 的坐标
的坐标
(3)如图2所示,若点![]() 为对称轴右侧抛物线上一点,连接
为对称轴右侧抛物线上一点,连接![]() ,以
,以![]() 为直角顶点,线段
为直角顶点,线段![]() 为较长直角边,构造两直角边比为
为较长直角边,构造两直角边比为![]() 的
的![]() ,是否存在点
,是否存在点![]() ,使点
,使点![]() 恰好落在直线
恰好落在直线![]() 上?若存在,请直接写出相应点
上?若存在,请直接写出相应点![]() 的横坐标;若不存在,请说明理由.
的横坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】在![]() 中,
中,![]() ,过点
,过点![]() 作直线
作直线![]() ,将
,将![]() 绕点C顺时针旋转得到
绕点C顺时针旋转得到![]() (点
(点![]() 的对应点分别是
的对应点分别是![]() ),射线
),射线![]() 分别交直线
分别交直线![]() 于点
于点![]() .
.
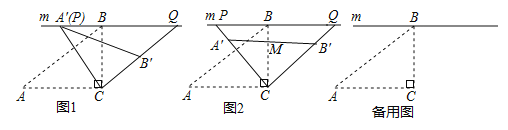
(1)问题发现:如图1所示,若![]() 与
与![]() 重合,则
重合,则![]() 的度数为_________________
的度数为_________________
(2)类比探究:如图2,所示,设![]() 与
与![]() 的交点为M,当M为
的交点为M,当M为![]() 中点时,求线段
中点时,求线段![]() 的长;
的长;
(3)拓展延伸:在旋转过程中,当点![]() 分别在
分别在![]() 的延长线上时,试探究四边形
的延长线上时,试探究四边形![]() 的面积是否存在最小值,若存在,直接写出四边形
的面积是否存在最小值,若存在,直接写出四边形![]() 的最小面积;若不存在,请说明理由
的最小面积;若不存在,请说明理由
查看答案和解析>>
科目: 来源: 题型:
【题目】襄阳市精准扶贫工作已进入攻坚阶段.贫困户张大爷在某单位的帮扶下,把一片坡地改造后种植了优质水果蓝莓,今年正式上市销售.在销售的30天中,第一天卖出20千克,为了扩大销量,采取了降价措施,以后每天比前一天多卖出4千克.第x天的售价为y元/千克,y关于x的函数解析式为![]() 且第12天的售价为32元/千克,第26天的售价为25元/千克.已知种植销售蓝莓的成木是18元/千克,每天的利润是W元(利润=销售收入﹣成本).
且第12天的售价为32元/千克,第26天的售价为25元/千克.已知种植销售蓝莓的成木是18元/千克,每天的利润是W元(利润=销售收入﹣成本).
(1)m= ,n= ;
(2)求销售蓝莓第几天时,当天的利润最大?最大利润是多少?
(3)在销售蓝莓的30天中,当天利润不低于870元的共有多少天?
查看答案和解析>>
科目: 来源: 题型:
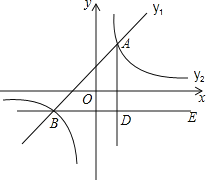
【题目】如图,在平面直角坐标系中,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点
的图象交于点![]() 和
和![]() .
.
![]() 求一次函数和反比例函数的表达式;
求一次函数和反比例函数的表达式;
![]() 请直接写出
请直接写出![]() 时,x的取值范围;
时,x的取值范围;
![]() 过点B作
过点B作![]() 轴,
轴,![]() 于点D,点C是直线BE上一点,若
于点D,点C是直线BE上一点,若![]() ,求点C的坐标.
,求点C的坐标.
查看答案和解析>>
科目: 来源: 题型:
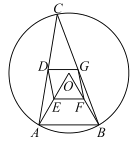
【题目】如图,![]() 是半径为4的
是半径为4的![]() 的内接三角形,连接
的内接三角形,连接![]() ,点
,点![]() 分别是
分别是![]() 的中点.
的中点.
(1)试判断四边形![]() 的形状,并说明理由;
的形状,并说明理由;
(2)填空:①若![]() ,当
,当![]() 时,四边形
时,四边形![]() 的面积是__________;②若
的面积是__________;②若![]() ,当
,当![]() 的度数为__________时,四边形
的度数为__________时,四边形![]() 是正方形.
是正方形.
查看答案和解析>>
科目: 来源: 题型:
【题目】学校开展“书香校园”活动以来,受到同学们的广泛关注,学校为了解全校学生课外阅读的情况,随机调查了部分学生在一周内借阅图书的次数,并制成如图不完整的统计表
学生借阅图书的次数
借阅图书的次数 | 0次 | 1次 | 2次 | 3次 | 4次及以上 |
人数 | 7 | 13 | a | 10 | 3 |
学生借阅图书的次数统计表

请你根据统计图表的信息,解答下列问题:
(1)a= ;b=
(2)该调查统计数据的中位数是__________次
(3)扇形统计图中,“3次”所对应的扇形圆心角度数是______________;
(4)若该校共有2000名学生,根据调查结果,估计该校学生在一周内借阅图书“4次以上”的人数
查看答案和解析>>
科目: 来源: 题型:
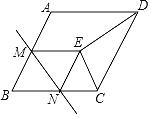
【题目】如图,在菱形ABCD中,∠B=60°,AB=2,M为边AB的中点,N为边BC上一动点(不与点B重合),将△BMN沿直线MN折叠,使点B落在点E处,连接DE、CE,当△CDE为等腰三角形时,BN的长为_____.
查看答案和解析>>
科目: 来源: 题型:
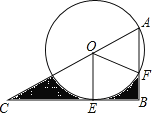
【题目】如图,Rt△ABC,∠B=90°,∠C=30°,O为AC上一点,OA=2,以O为圆心,以OA为半径的圆与CB相切于点E,与AB相交于点F,连接OE、OF,则图中阴影部分的面积是_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com