
科目: 来源: 题型:
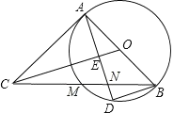
【题目】如图,AB是⊙O的直径,CA与⊙O相切于点A,且CA=BA.连接OC,过点A作AD⊥OC于点E,交⊙O于点D,连接DB.
(1)求证:△ACE≌△BAD;
(2)连接CB交⊙O于点M,交AD于点N.若AD=4,求MN的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】为迎接2022年冬奥会,鼓励更多的学生参与到志愿服务中来,甲、乙两所学校组织了志愿服务团队选拔活动,经过初选,两所学校各有400名学生进入综合素质展示环节.为了了解两所学校这些学生的整体情况,从两校进人综合素质展示环节的学生中分别随机抽取了50名学生的综合素质展示成绩(百分制),并对数据(成绩)进行整理、描述和分析.下面给出了部分信息.
a.甲学校学生成绩的频数分布直方图如下(数据分成6组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() );
);
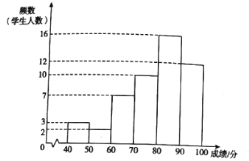
b.甲学校学生成绩在![]() 这一组的是:
这一组的是:
80 80 81 81.5 82 83 83 84
85 86 86.5 87 88 88.5 89 89
c.乙学校学生成绩的平均数、中位数、众数、优秀率(85分及以上为优秀)如下:
平均数 | 中位数 | 众数 | 优秀率 |
83.3 | 84 | 78 | 46% |
根据以上信息,回答下列问题:
(1)甲学校学生A,乙学校学生B的综合素质展示成绩同为83分,这两人在本校学生中的综合素质展示排名更靠前的是______(填“A”或“B”);
(2)根据上述信息,推断_____学校综合素质展示的水平更高,理由为_____(至少从两个不同的角度说明推断的合理性);
(3)若每所学校综合素质展示的前120名学生将被选入志愿服务团队,预估甲学校分数至少达到____分的学生才可以入选.
查看答案和解析>>
科目: 来源: 题型:
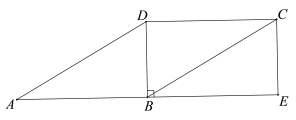
【题目】如图,在□ABCD中,∠ABD=90°,延长AB至点E,使BE=AB,连接CE.
(1)求证:四边形BECD是矩形;
(2)连接DE交BC于点F,连接AF,若CE=2,∠DAB=30°,求AF的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】5G网络是第五代移动通信网络,它将推动我国数字经济发展迈上新台阶. 据预测,2020年到2030年中国5G直接经济产出和间接经济产出的情况如下图所示.
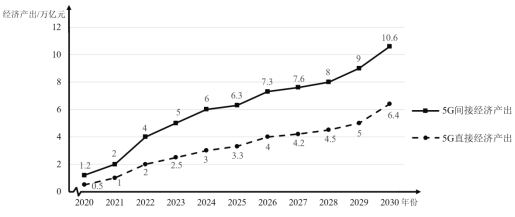
根据上图提供的信息,下列推断不合理的是( )
A.2030年5G间接经济产出比5G直接经济产出多4.2万亿元
B.2020年到2030年,5G直接经济产出和5G间接经济产出都是逐年增长
C.2030年5G直接经济产出约为2020年5G直接经济产出的13倍
D.2022年到2023年与2023年到2024年5G间接经济产出的增长率相同
查看答案和解析>>
科目: 来源: 题型:
【题目】广阔无垠的太空中有无数颗恒星,其中离太阳系最近的一颗恒星称为“比邻星”,它距离太阳系约4.2光年.光年是天文学中一种计量天体时空距离的长度单位,1光年约为9500000000000千米.则“比邻星”距离太阳系约为( )
A. ![]() 千米B.
千米B. ![]() 千米C.
千米C. ![]() 千米D.
千米D. ![]() 千米
千米
查看答案和解析>>
科目: 来源: 题型:
【题目】平面直角坐标系![]() 中有点
中有点![]() 和某一函数图象
和某一函数图象![]() ,过点
,过点![]() 作
作![]() 轴的垂线,交图象
轴的垂线,交图象![]() 于点
于点![]() ,设点
,设点![]() ,
,![]() 的纵坐标分别为
的纵坐标分别为![]() ,
,![]() .如果
.如果![]() ,那么称点
,那么称点![]() 为图象
为图象![]() 的上位点;如果
的上位点;如果![]() ,那么称点
,那么称点![]() 为图象
为图象![]() 的图上点;如果
的图上点;如果![]() ,那么称点
,那么称点![]() 为图象
为图象![]() 的下位点.
的下位点.
(1)已知抛物线![]() .
.
① 在点A(-1,0),B(0,-2),C(2,3)中,是抛物线的上位点的是 ;
② 如果点![]() 是直线
是直线![]() 的图上点,且为抛物线的上位点,求点
的图上点,且为抛物线的上位点,求点![]() 的横坐标
的横坐标![]() 的取值范围;
的取值范围;
(2)将直线![]() 在直线
在直线![]() 下方的部分沿直线
下方的部分沿直线![]() 翻折,直线
翻折,直线![]() 的其余部分保持不变,得到一个新的图象,记作图象
的其余部分保持不变,得到一个新的图象,记作图象![]() .⊙
.⊙![]() 的圆心
的圆心![]() 在
在![]() 轴上,半径为
轴上,半径为![]() .如果在图象
.如果在图象![]() 和⊙
和⊙![]() 上分别存在点
上分别存在点![]() 和点F,使得线段EF上同时存在图象
和点F,使得线段EF上同时存在图象![]() 的上位点,图上点和下位点,求圆心
的上位点,图上点和下位点,求圆心![]() 的横坐标
的横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() :
:![]() 沿
沿![]() 轴翻折得到抛物线
轴翻折得到抛物线![]() .
.
(1)求抛物线![]() 的顶点坐标;
的顶点坐标;
(2)横、纵坐标都是整数的点叫做整点.
① 当![]() 时,求抛物线
时,求抛物线![]() 和
和![]() 围成的封闭区域内(包括边界)整点的个数;
围成的封闭区域内(包括边界)整点的个数;
② 如果抛物线C1和C2围成的封闭区域内(包括边界)恰有![]() 个整点,求m取值范围.
个整点,求m取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】在二次函数的学习中,教材有如下内容:
例1 函数图象求一元二次方程![]() 的近似解(精确到0.1).
的近似解(精确到0.1).
解:设有二次函数![]() ,列表并作出它的图象(图1).
,列表并作出它的图象(图1).
| … |
| 0 | 1 | 2 | 3 | 4 | 5 | … |
| … |
|
|
|
|
|
|
| … |
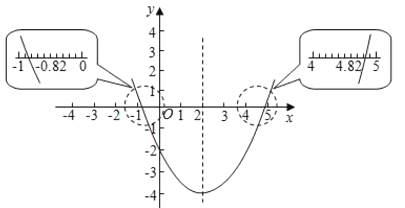
观察抛物线和![]() 轴交点的位置,估计出交点的横坐标分别约为
轴交点的位置,估计出交点的横坐标分别约为![]() 和4.8,所以得出方程精确到0.1的近似解为
和4.8,所以得出方程精确到0.1的近似解为![]() ,
,![]() ,利用二次函数
,利用二次函数![]() 的图象求出一元二次方程
的图象求出一元二次方程![]() 的解的方法称为图象法,这种方法常用来求方程的近似解.
的解的方法称为图象法,这种方法常用来求方程的近似解.
小聪和小明通过例题的学习,体会到利用函数图象可以求出方程的近似解.于是他们尝试利用图象法探宄方程![]() 的近似解,做法如下:
的近似解,做法如下:
小聪的做法:令函数![]() ,列表并画出函数的图象,借助图象得到方程
,列表并画出函数的图象,借助图象得到方程![]() 的近似解.
的近似解.
小明的做法:因为![]() ,所以先将方程
,所以先将方程![]() 的两边同时除以
的两边同时除以![]() ,变形得到方程
,变形得到方程![]() ,再令函数
,再令函数![]() 和
和![]() ,列表并画出这两个函数的图象,借助图象得到方程
,列表并画出这两个函数的图象,借助图象得到方程![]() 的近似解.
的近似解.
请你选择小聪或小明的做法,求出方程![]() 的近似解(精确到0.1).
的近似解(精确到0.1).
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,点O为∠ABC的边![]() 上的一点,过点O作OM⊥AB于点
上的一点,过点O作OM⊥AB于点![]() ,到点
,到点![]() 的距离等于线段OM的长的所有点组成图形
的距离等于线段OM的长的所有点组成图形![]() .图形W与射线
.图形W与射线![]() 交于E,F两点(点在点F的左侧).
交于E,F两点(点在点F的左侧).
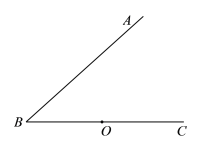
(1)过点![]() 作
作![]() 于点
于点![]() ,如果BE=2,
,如果BE=2,![]() ,求MH的长;
,求MH的长;
(2)将射线BC绕点B顺时针旋转得到射线BD,使得∠![]()
![]() ,判断射线BD与图形
,判断射线BD与图形![]() 公共点的个数,并证明.
公共点的个数,并证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com