
科目: 来源: 题型:
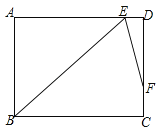
【题目】在矩形ABCD中,∠B的角平分线BE与AD交于点E,∠BED的角平分线EF与DC交于点F,若AB=9,DF=2FC,则BC=____.(结果保留根号)
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图1,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 、
、![]() (
(![]() 左
左![]() 右),与
右),与![]() 轴交于点
轴交于点![]() ,且
,且![]() .
.
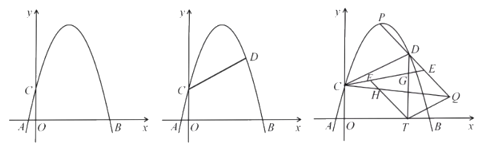
(1)求抛物线的解析式;
(2)如图2,点![]() 在第一象限抛物线上,连接
在第一象限抛物线上,连接![]() ,若
,若![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)在(2)的条件下,如图3,过点![]() 作
作![]() 轴,线段
轴,线段![]() 经过点
经过点![]() ,与抛物线交于点
,与抛物线交于点![]() ,连接
,连接![]() 、
、![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 上,连接
上,连接![]() ,交
,交![]() 于点
于点![]() ,点
,点![]() 在
在![]() 上,连接
上,连接![]() ,交
,交![]() 于点
于点![]() ,若
,若![]() ,
,![]() ,
,![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,![]() ,
,![]() 是
是![]() 的直径,点
的直径,点![]() 在
在![]() 上,连接
上,连接![]() ,
,![]() .
.
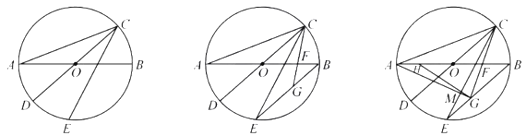
(1)求证:![]() 平分
平分![]() ;
;
(2)如图2,连接![]() ,点
,点![]() 在
在![]() 上,连接
上,连接![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,求证:
,求证:![]() ;
;
(3)在(2)的条件下,点![]() 在
在![]() 上,连接
上,连接![]() ,
,![]() ,
,![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,若
,若![]() ,
,![]() ,
,![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】光明中学在体育用品商店购进![]() 、
、![]() 两种型号的冰刀,购买
两种型号的冰刀,购买![]() 种型号冰刀花费2400元,购买
种型号冰刀花费2400元,购买![]() 种型号冰刀花费了l950元,且购买
种型号冰刀花费了l950元,且购买![]() 种型号冰刀数量是购买
种型号冰刀数量是购买![]() 种型号冰刀数量的2倍,已知购买一副
种型号冰刀数量的2倍,已知购买一副![]() 种型号冰刀比购买一副
种型号冰刀比购买一副![]() 种型号冰刀多花50元.
种型号冰刀多花50元.
(1)求购买一副![]() 种型号、一副
种型号、一副![]() 种型号的冰刀各需多少元?
种型号的冰刀各需多少元?
(2)该学校决定再次购进![]() 、
、![]() 两种型号冰刀共30副,恰逢百货商场对两种型号冰刀的售价进行调整,
两种型号冰刀共30副,恰逢百货商场对两种型号冰刀的售价进行调整,![]() 种型号冰刀售价比第一次购买时提高了
种型号冰刀售价比第一次购买时提高了![]() ,
,![]() 种型号冰刀按第一次购买时售价的9折出售,如果这所中学此次购买
种型号冰刀按第一次购买时售价的9折出售,如果这所中学此次购买![]() 、
、![]() 两种型号冰刀的总费用不超过3220元,那么该学校此次最多可购买多少副
两种型号冰刀的总费用不超过3220元,那么该学校此次最多可购买多少副![]() 种型号冰刀?
种型号冰刀?
查看答案和解析>>
科目: 来源: 题型:
【题目】阳光中学约有学生3000名,为了增强学生体质,学校决定举行体育比赛,在篮球、足球、排球和乒乓球这四项球类运动中选择一项球类进行比赛,对学生开展了随机调查,并将结果绘制成如下不完整的统计图.
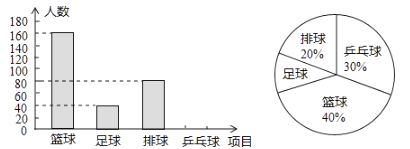
请根据以上信息,完成下列问题:
(1)本次调查共抽取了多少名学生?
(2)求在被调查的学生中,最喜爱乒乓球的人数,并补全条形统计图;
(3)请你估计阳光中学的学生中最喜爱篮球运动的学生人数约有多少名?
查看答案和解析>>
科目: 来源: 题型:
【题目】若抛物线![]() (
(![]() 是常数,
是常数,![]() )与直线
)与直线![]() 都经过
都经过![]() 轴上的一点
轴上的一点![]() ,且抛物线
,且抛物线![]() 的顶点
的顶点![]() 在直线
在直线![]() 上,则称此直线
上,则称此直线![]() 与该抛物线
与该抛物线![]() 具有“一带一路”关系.此时,直线
具有“一带一路”关系.此时,直线![]() 叫做抛物线
叫做抛物线![]() 的“带线”,抛物线
的“带线”,抛物线![]() 叫做直线
叫做直线![]() 的“路线”.
的“路线”.
(1)若直线![]() 与抛物线
与抛物线![]() 具有“一带一路”关系,求
具有“一带一路”关系,求![]() 的值;
的值;
(2)若某“路线”![]() 的顶点在反比例函数
的顶点在反比例函数![]() 的图象上,它的“带线”
的图象上,它的“带线”![]() 的解析式为
的解析式为![]() ,求此“路线”
,求此“路线”![]() 的解析式;
的解析式;
(3)当常数![]() 满足
满足![]() 时,请直接写出抛物线
时,请直接写出抛物线![]() :
:![]() 的“带线”
的“带线”![]() 与
与![]() 轴,
轴,![]() 轴所围成的三角形面积S的取值范围.
轴所围成的三角形面积S的取值范围.
查看答案和解析>>
科目: 来源: 题型:
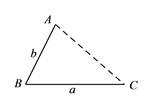
【题目】(1)发现
如图,点![]() 为线段
为线段![]() 外一动点,且
外一动点,且![]() ,
,![]() .
.
填空:当点![]() 位于____________时,线段
位于____________时,线段![]() 的长取得最大值,且最大值为_________.(用含
的长取得最大值,且最大值为_________.(用含![]() ,
,![]() 的式子表示)
的式子表示)
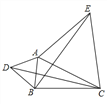
(2)应用
点![]() 为线段
为线段![]() 外一动点,且
外一动点,且![]() ,
,![]() .如图所示,分别以
.如图所示,分别以![]() ,
,![]() 为边,作等边三角形
为边,作等边三角形![]() 和等边三角形
和等边三角形![]() ,连接
,连接![]() ,
,![]() .
.
①找出图中与![]() 相等的线段,并说明理由;
相等的线段,并说明理由;
②直接写出线段![]() 长的最大值.
长的最大值.
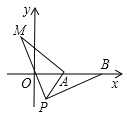
(3)拓展
如图,在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 为线段
为线段![]() 外一动点,且
外一动点,且![]() ,
,![]() ,
,![]() ,求线段
,求线段![]() 长的最大值及此时点
长的最大值及此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴交于A,B两点(点A在点B左侧)
轴交于A,B两点(点A在点B左侧)
(1)求抛物线的顶点坐标(用含![]() 的代数式表示);
的代数式表示);
(2)求线段AB的长;
(3)抛物线与![]() 轴交于点C(点C不与原点
轴交于点C(点C不与原点![]() 重合),若
重合),若![]() 的面积始终小于
的面积始终小于![]() 的面积,求
的面积,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com