
【题目】阳光中学约有学生3000名,为了增强学生体质,学校决定举行体育比赛,在篮球、足球、排球和乒乓球这四项球类运动中选择一项球类进行比赛,对学生开展了随机调查,并将结果绘制成如下不完整的统计图.
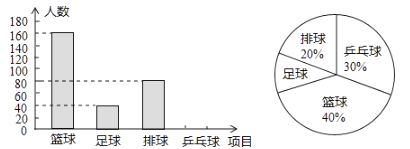
请根据以上信息,完成下列问题:
(1)本次调查共抽取了多少名学生?
(2)求在被调查的学生中,最喜爱乒乓球的人数,并补全条形统计图;
(3)请你估计阳光中学的学生中最喜爱篮球运动的学生人数约有多少名?
科目:初中数学 来源: 题型:
【题目】定义:把函数![]() 的图像绕点
的图像绕点![]() 旋转180°,得到新函数
旋转180°,得到新函数![]() 的图像,我们称
的图像,我们称![]() 是
是![]() 关于点
关于点![]() 的相关函数.
的相关函数.![]() 的图像的对称轴为直线
的图像的对称轴为直线![]() .例如:当
.例如:当![]() 时,函数
时,函数![]() 关于点
关于点![]() 的相关函数为
的相关函数为![]() .
.
(1)填空:![]() 的值为________(用含
的值为________(用含![]() 的代数式表示);
的代数式表示);
(2)若![]() ,
,![]() ,当
,当![]() 时,函数
时,函数![]() 的最大值为
的最大值为![]() ,最小值为
,最小值为![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
(3)当![]() 时,
时,![]() 的图像与
的图像与![]() 轴相交于
轴相交于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的右侧),与
的右侧),与![]() 轴相交于点
轴相交于点![]() .把线段
.把线段![]() 绕原点
绕原点![]() 顺时针旋转90°,得到它的对应线段
顺时针旋转90°,得到它的对应线段![]() .若线段
.若线段![]() 与
与![]() 的图像有公共点,结合函数图像,求
的图像有公共点,结合函数图像,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 交x轴于点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D,下列四个结论:
交x轴于点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D,下列四个结论:
①点C的坐标为(0,m);
②当m=0时,△ABD是等腰直角三角形;
③若a=-1,则b=4;
④抛物线上有两点P(![]() ,
,![]() )和Q(
)和Q(![]() ,
,![]() ),若
),若![]() <1<
<1<![]() ,且
,且![]() +
+![]() >2,则
>2,则![]() >
>![]() .
.
其中结论正确的序号是( )

A.①②B.①②③C.①②④D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
上课时孙老师提出这样一个问题:对于任意实数![]() ,关于
,关于![]() 的不等式
的不等式![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
小明的思路是:原不等式等价于![]() ,设函数
,设函数![]() ,
,![]() ,画出两个函数的图象的示意图,于是原问题转化为函数
,画出两个函数的图象的示意图,于是原问题转化为函数![]() 的图象在
的图象在![]() 的图象上方时
的图象上方时![]() 的取值范围.
的取值范围.

请结合小明的思路回答:
对于任意实数![]() ,关于
,关于![]() 的不等式
的不等式![]() 恒成立,则
恒成立,则![]() 的取值范围是_____.
的取值范围是_____.
参考小明思考问题的方法,解决问题:
关于![]() 的方程
的方程![]() 在
在![]() 范围内有两个解,求
范围内有两个解,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,∠B的角平分线BE与AD交于点E,∠BED的角平分线EF与DC交于点F,若AB=9,DF=2FC,则BC=____.(结果保留根号)
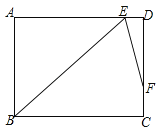
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)如图,在直角坐标系中,Rt△OAB的直角顶点A在x轴上,OA=4,AB=3.动点M从点A出发,以每秒1个单位长度的速度,沿AO向终点O移动;同时点N从点O出发,以每秒1.25个单位长度的速度,沿OB向终点B移动.当两个动点运动了x秒(0<x<4)时,解答下列问题:
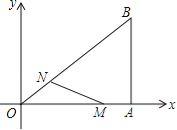
(1)求点N的坐标(用含x的代数式表示);
(2)设△OMN的面积是S,求S与x之间的函数表达式;当x为何值时,S有最大值?最大值是多少?
(3)在两个动点运动过程中,是否存在某一时刻,使△OMN是直角三角形?若存在,求出x的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,△AOB是等腰直角三角形,∠AOB=90°,点A(2,1).
(1)求点B的坐标;
(2)求经过A、O、B三点的抛物线的函数表达式;
(3)在(2)所求的抛物线上,是否存在一点P,使四边形ABOP的面积最大?若存在,求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com