
科目: 来源: 题型:
【题目】为了了解某校七年级学生每周上网的时间,甲、乙两名学生进行了抽样调查.甲同学调查了七年级电脑爱好者中40名学生每周上网的时间;乙同学从全校800名七年级学生中随机抽取了40名学生,调查了每周上网的时间.甲、乙同学各自整理的样本数据如表:
上网时间t(小时/周) | 甲学生抽样人数(人) | 乙学生抽样人数(人) |
0≤t<1.5 | 6 | 22 |
1.5≤t<2.5 | 10 | 10 |
2.5≤t<3.5 | 16 | 6 |
t≥3.5 | 8 | 2 |
(1)你认为哪名学生抽取的样本不合理,请说明理由.
(2)请你根据抽取样本合理的学生的数据,将调查结果绘制成合适的统计图(绘制一种即可).
(3)专家建议每周上网2.5小时以上(含2.5小时)的学生应适当减少上网的时间,估计该校全体七年级学生中应适当减少上网的时间的人数.
查看答案和解析>>
科目: 来源: 题型:
【题目】题目:某校七年级学生乘车去参加社会实践活动,若每辆客车乘50人,还有12人不能上车;若每辆客车乘55人,则最后一辆空了8个座位,求该校租这种客车的辆数:
根据题意,小明、小红分别列出了尚不完整的方程如下:
小明列出不完整的方程为![]()
小红列出不完整的方程为![]()
(说明:其中“![]() ”表示运算符号,“
”表示运算符号,“![]() ”表示数字):
”表示数字):
(1)小明所列方程中![]() 表示的意义是________________________;
表示的意义是________________________;
小红所列方程中![]() 表示的意义是___________________________;
表示的意义是___________________________;
(2)选择两位同学的其中一位学生的做法,将其补充完整,并完整地解答这道题.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,线段AB的两个端点的坐标分别为(-1,2)、(1,1).抛物线y=ax2+bx+c(a≠0)与x轴交于C、D两点,点C在点D左侧,当顶点在线段AB上移动时,点C横坐标的最小值为-2.在抛物线移动过程中,a-b+c的最小值是____.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,在Rt△ABC中,∠ACB=90°,边BC在x轴上,点B在点C的右侧,顶点A和AB的中点D在函数![]() 的图象上.若△ABC的面积为12,则k的值为( )
的图象上.若△ABC的面积为12,则k的值为( )
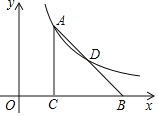
A.24B.12C.6D.6
查看答案和解析>>
科目: 来源: 题型:
【题目】《九章算术》是我国东汉初年编订的一部数学经典著作.在它的“方程”一章里,一次方程组是由算筹布置而成的.《九章算术》中的算筹图是竖排的,为看图方便,我们把它改为横排,如图1、图2.图中各行从左到右列出的算筹数分别表示未知数x,y的系数与相应的常数项.把图1所示的算筹图用我们现在所熟悉的方程组形式表述出来,就是![]() ,类似地,图2所示的算筹图我们可以表述为( )
,类似地,图2所示的算筹图我们可以表述为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】函数y1=kx2+ax+a的图象与x轴交于点A,B(点A在点B的左侧),函数y2=kx2+bx+b,的图象与x轴交于点C,D(点C在点D的左侧),其中k≠0,a≠b.
(1)求证:函数y1与y2的图象交点落在一条定直线上;
(2)若AB=CD,求a,b和k应满足的关系式;
(3)是否存在函数y1和y2,使得B,C为线段AD的三等分点?若存在,求![]() 的值,若不存在,说明理由
的值,若不存在,说明理由
查看答案和解析>>
科目: 来源: 题型:
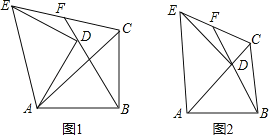
【题目】如图1,在Rt△ABC中,∠ABC=90°,AB=BC,将△ABC绕点A逆时针旋转,得到△ADE,旋转角为α(0°<α<90°),连接BD交CE于点F.
(1)如图2,当α=45°时,求证:CF=EF;
(2)在旋转过程中,①问(1)中的结论是否仍然成立?证明你的结论;②连接CD,当△CDF为等腰直角三角形时,求tan![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】在△PQN中,若∠P=![]() ∠Q+α(0°<α≤25°),则称△PQN为“差角三角形”,且∠P是 ∠Q的“差角”.
∠Q+α(0°<α≤25°),则称△PQN为“差角三角形”,且∠P是 ∠Q的“差角”.
(1)已知△ABC是等边三角形,判断△ABC是否为“差角三角形”,并说明理由;
(2)在△ABC中,∠C=90°,50°≤∠B≤70°,判断△ABC是否为“差角三角形”,若是,请写出所有的“差角”并说明理由;若不是,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
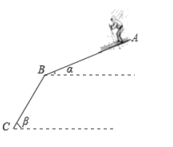
【题目】2022年在北京将举办第24届冬季奥运会,很多学校都开展了冰雪项目学习.如图,滑雪轨道由AB,BC两部分组成,AB,BC的长度都为200米,一位同学乘滑雪板沿此轨道由A点滑到了C点,若AB与水平面的夹角α为20°,BC与水平面的夹角β为45°,则他下降的高度为多少米.(结果保留整数)(参考数据sin20°≈0.342,cos20°≈0.940,tan20°≈0.364)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com