
科目: 来源: 题型:
【题目】已知:如图1,六边形![]() 中,
中,![]() ,
,![]() ,
,![]() .
.
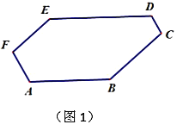
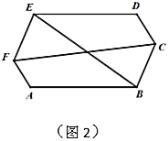
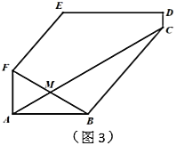
(1)找出这个六边形中所有相等的内角_______.证明其中的一个结论.
(2)如果![]() ,证明对角线
,证明对角线![]() ,
,![]() 互相平分;
互相平分;
(3)如图,如果![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,对角线
,对角线![]() 平分对角线
平分对角线![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】新型冠状肺炎给人类带来了灾难.口罩是抗击新冠肺炎的重要战略物资,国家在必要时进行价格限制,以保持价格稳定.某公司生产的口罩售价与天数的函数关系如图所示(曲线部分是以![]() 轴为对称轴的抛物线一部分).
轴为对称轴的抛物线一部分).
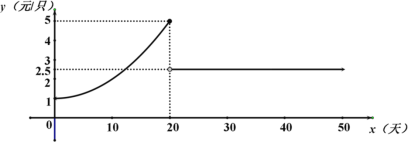
(1)求口罩销售价格![]() (元)与天数
(元)与天数![]() (天)之间的函数关系式;
(天)之间的函数关系式;
(2)若这种口罩每只成本![]() (元)与天数
(元)与天数![]() 之间的关系为:
之间的关系为: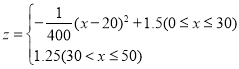 .那么这种口罩在第几天售出后单只利润最大?最大利润为多少?
.那么这种口罩在第几天售出后单只利润最大?最大利润为多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四边形![]() 中,
中,![]() ,以
,以![]() 为直径的
为直径的![]() 经过点
经过点![]() ,连接
,连接![]() ,
,![]() 交于点
交于点![]() .
.

(1)证明:![]() ;
;
(2)若![]() ,证明:
,证明:![]() 是
是![]() 的切线;
的切线;
(3)在(2)条件下,连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,若
,若![]() 的直径为
的直径为![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】甲乙两人依次测量同一圆柱体工件的横截面直径(单位:![]() ),测得的数据分别如表1、表2.
),测得的数据分别如表1、表2.
表1:甲的测量数据
测量数据 | 9.8 | 9.9 | 10 | 10.1 | 10.3 |
频数 | 1 | 3 | 3 | 2 | 1 |
表2:乙的测量数据
测量数据 | 9.7 | 9.8 | 10 | 10.1 | 10.3 |
频数 | 1 | 2 | 3 | 2 | 2 |
(1)如果在这些测量数据中选择一个数据作为工件直径的估计值,应该是那个数据?请说明理由.
(2)如果甲再测量一次,求他测量出的数据恰好是估计值的概率;
(3)请直接判断甲乙两人谁的测量技术更好______(填甲或乙),你选择的统计量是_______.
查看答案和解析>>
科目: 来源: 题型:
【题目】某商场计划购进![]() ,
,![]() 两种新型节能台灯共120盏,这两种台灯的进价和售价如表所示:
两种新型节能台灯共120盏,这两种台灯的进价和售价如表所示:
价格 类型 | 进价(元/盏) | 售价(元/盏) |
| 40 | 55 |
| 60 | 80 |
(1)若商场恰好用完预计进货款5500元,则应这购进两种台灯各多少盏?
(2)若商场规定![]() 型台灯的进货数量不超过
型台灯的进货数量不超过![]() 型台灯数量的3倍,应怎样进货才能使商场在销售完这两种台灯时获得的毛利润最多?最多毛利润为多少元?(毛利润=销售收入-进货成本).
型台灯数量的3倍,应怎样进货才能使商场在销售完这两种台灯时获得的毛利润最多?最多毛利润为多少元?(毛利润=销售收入-进货成本).
查看答案和解析>>
科目: 来源: 题型:
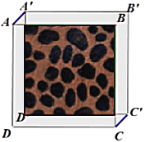
【题目】如图正方形![]() 先向右平移1个单位长度,再向上平移1个单位长度,得到正方形
先向右平移1个单位长度,再向上平移1个单位长度,得到正方形![]() ,形成了中间深色的正方形及四周浅色的边框,已知正方形
,形成了中间深色的正方形及四周浅色的边框,已知正方形![]() 的面积为16,则四周浅色边框的面积是________.
的面积为16,则四周浅色边框的面积是________.
查看答案和解析>>
科目: 来源: 题型:
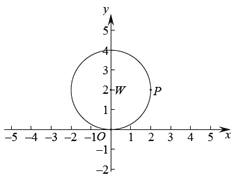
【题目】如图,在平面直角坐标系![]() 中,存在半径为2,圆心为(0,2)的
中,存在半径为2,圆心为(0,2)的![]() ,点
,点![]() 为
为![]() 上的任意一点,线段
上的任意一点,线段![]() 绕点
绕点![]() 逆时针旋转90°得到线段
逆时针旋转90°得到线段![]() ,如果点
,如果点![]() 在线段
在线段![]() 上,那么称点
上,那么称点![]() 为
为![]() 的“限距点”.
的“限距点”.
(1)在点![]() 中,
中,![]() 的“限距点”为____________________________;
的“限距点”为____________________________;
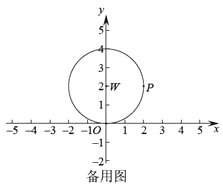
(2)如果过点![]() 且平行于
且平行于![]() 轴的直线
轴的直线![]() 上始终存在
上始终存在![]() 的“限距点”,画出示意图并直接写出
的“限距点”,画出示意图并直接写出![]() 的取值范围;
的取值范围;
(3)![]() 的圆心为
的圆心为![]() ,半径为1,如果
,半径为1,如果![]() 上始终存在
上始终存在![]() 的“限距点”,请直接写出
的“限距点”,请直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在正方形![]() 中,点
中,点![]() 分别是
分别是![]() 上的两个动点(不与点
上的两个动点(不与点![]() 重合),且
重合),且![]() ,延长
,延长![]() 到
到![]() ,使
,使![]() ,连接
,连接![]() .
.
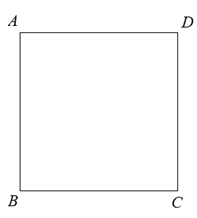
(1)依题意将图形补全;
(2)小华通过观察、实验、提出猜想:在点![]() 运动过程中,始终有
运动过程中,始终有![]() .经过与同学们充分讨论,形成了几种证明的想法:
.经过与同学们充分讨论,形成了几种证明的想法:
想法一:连接![]() ,证明
,证明![]() 是等腰直角三角形;
是等腰直角三角形;
想法二:过点![]() 作
作![]() 的垂线,交
的垂线,交![]() 的延长线于
的延长线于![]() ,可得
,可得![]() 是等腰直角三角形,证明
是等腰直角三角形,证明![]() ;
;
……
请参考以上想法,帮助小华证明![]() .(写出一种方法即可)
.(写出一种方法即可)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com