
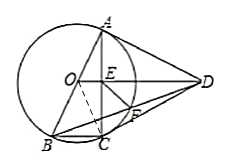
【题目】如图,在四边形![]() 中,
中,![]() ,以
,以![]() 为直径的
为直径的![]() 经过点
经过点![]() ,连接
,连接![]() ,
,![]() 交于点
交于点![]() .
.

(1)证明:![]() ;
;
(2)若![]() ,证明:
,证明:![]() 是
是![]() 的切线;
的切线;
(3)在(2)条件下,连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,若
,若![]() 的直径为
的直径为![]() ,求
,求![]() 的长.
的长.
【答案】(1)见解析;(2)见解析;(3)![]() .
.
【解析】
(1)连接OC,证△OAD≌△OCD得∠ADO=∠CDO,又AD=CD知AE=CE;
(2)设BC=a、则AC=2a、AD=AB=![]() =
=![]() a,证OE为中位线知OE=
a,证OE为中位线知OE=![]() a、AE=CE=
a、AE=CE=![]() AC=a,进一步求得DE=
AC=a,进一步求得DE=![]() =2a,再在△AOD中利用勾股定理逆定理证∠OAD=90°即可得;
=2a,再在△AOD中利用勾股定理逆定理证∠OAD=90°即可得;
(3)先证△AFD∽△BAD得DFBD=AD2①,再证△AED∽△OAD得ODDE=AD2②,由①②得DFBD=ODDE,即![]() ,结合∠EDF=∠BDO知△EDF∽△BDO,据此可得
,结合∠EDF=∠BDO知△EDF∽△BDO,据此可得![]() ,结合(2)可得相关线段的长,代入计算可得.
,结合(2)可得相关线段的长,代入计算可得.
(1)连接![]() ,
,
在![]() 和
和![]() 中,
中,
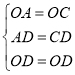 ,
,
∴![]() ,
,
∴![]()
∴![]()
(2)由(1)得![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() 为
为![]() 的直径,
的直径,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴设![]() 、则
、则![]() ,
,
∴![]() ,
,
∵![]() ,且
,且![]() ,
,
∴![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,
在![]() 中,
中,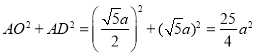 ,
,
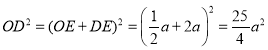 ,
,
∴![]() ,
,
∴![]() ,
,
则![]() 与
与![]() 相切;
相切;
(3)连接![]() ,
,
∵![]() 是
是![]() 的直径,
的直径,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ①,
①,
又∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ②,
②,
由①②可得![]() ,即
,即![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,即
,即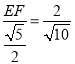 ,
,
解得:![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,点D是
,点D是![]() 外一点,点D与点C在直线
外一点,点D与点C在直线![]() 的异侧,且点
的异侧,且点![]() 不共线,连接
不共线,连接![]() .
.


(1)如图1,当![]() 时,画出图形,直接写出
时,画出图形,直接写出![]() 之间的数量关系;
之间的数量关系;
(2)当![]() 时,利用图2,继续探究
时,利用图2,继续探究![]() 之间的数量关系并证明;
之间的数量关系并证明;
(提示:尝试运用图形变换,将要研究的有关线段尽可能转移到一个三角形中)
(3)当![]() 时,进一步探究
时,进一步探究![]() 之间的数量关系,并用含
之间的数量关系,并用含![]() 的等式直接表示出它们之间的关系.
的等式直接表示出它们之间的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]()
(1)作边![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() (尺规作图,不写作法,保留作图痕迹).
(尺规作图,不写作法,保留作图痕迹).
(2)在(1)的条件下,连接![]() ,判断线段
,判断线段![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙、丁四位同学进行一次乒乓球单打比赛,要从中选出两位同学打第一场比赛.
(1)请用树状图法或列表法,求恰好选中甲、乙两位同学的概率.
(2)若已确定甲打第一场,再从其余三位同学中随机选取一位,求恰好选中乙同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五一黄金周,小张一家自驾去某景点旅行.已知汽车油箱的容积为50L,小张爸爸把油箱加满油后到了离加油站200km的某景点,第二天沿原路返回.
(1)油箱加满油后,求汽车行驶的总路程s(单位:km)与平均耗油量b(单位L/km)的函数关系式;
(2)小张爸爸以平均每千米耗油0.1L的速度驾驶到达目的地,返程时由于下雨,降低了车速,此时平均每千米的耗油量增加了一倍.如果小张爸爸始终以此速度行驶,不需要加油能否返回原加油站?如果不能,至少还需加多少油?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在日常生活中,我们经常看到一些窗户上安装着遮阳篷,如图![]() ,现在要为一个面向正南的窗户设计安装一个遮阳篷,已知该地区冬天正午太阳最低时,光线与水平线的夹角为
,现在要为一个面向正南的窗户设计安装一个遮阳篷,已知该地区冬天正午太阳最低时,光线与水平线的夹角为![]() ;夏天正午太阳最高时,光线与水平线的夹角为
;夏天正午太阳最高时,光线与水平线的夹角为![]() .把图
.把图![]() 画成图
画成图![]() ,其中
,其中![]() 表示窗户的高,
表示窗户的高,![]() 表示直角形遮阳篷.
表示直角形遮阳篷.
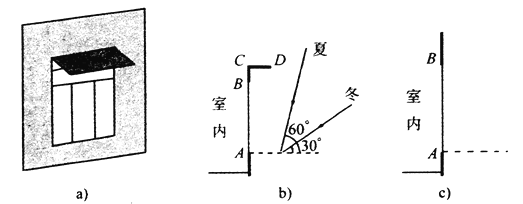
(1)遮阳篷![]() 怎样设计,才能正好在冬天正午太阳最低时光线最大限度地射入室内,而夏天正午太阳最高时光线刚好不射入室内?请在图
怎样设计,才能正好在冬天正午太阳最低时光线最大限度地射入室内,而夏天正午太阳最高时光线刚好不射入室内?请在图![]() 中画图表示;
中画图表示;
(2)已知![]() ,在
,在![]() 的条件下,求出
的条件下,求出![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司经过市场调查,发现某种运动服的销量与售价是一次函数关系,具体信息如下表:
售价(元/件) | 200 | 210 | 220 | 230 | … |
月销量(件) | 200 | 180 | 160 | 140 | … |
已知该运动服的进价为每件150元.
(1)售价为![]() 元,月销量为
元,月销量为![]() 件;
件;
①求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
②若销售该运动服的月利润为![]() 元,求
元,求![]() 关于
关于![]() 的函数关系式,并求月利润最大时的售价;
的函数关系式,并求月利润最大时的售价;
(2)由于运动服进价降低了![]() 元,商家决定回馈顾客,打折销售,这时月销量与调整后的售价仍满足(1)中函数关系式.结果发现,此时月利润最大时的售价比调整前月利润最大时的售价低15元,则
元,商家决定回馈顾客,打折销售,这时月销量与调整后的售价仍满足(1)中函数关系式.结果发现,此时月利润最大时的售价比调整前月利润最大时的售价低15元,则![]() 的值是多少?
的值是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com