
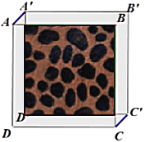
【题目】如图正方形![]() 先向右平移1个单位长度,再向上平移1个单位长度,得到正方形
先向右平移1个单位长度,再向上平移1个单位长度,得到正方形![]() ,形成了中间深色的正方形及四周浅色的边框,已知正方形
,形成了中间深色的正方形及四周浅色的边框,已知正方形![]() 的面积为16,则四周浅色边框的面积是________.
的面积为16,则四周浅色边框的面积是________.
 小学课时特训系列答案
小学课时特训系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,反比例函数
中,反比例函数![]() 的图象经过点
的图象经过点![]() ,直线
,直线![]() 与x轴交于点
与x轴交于点![]() .
.
(1)求![]() 的值;
的值;
(2)已知点![]() ,过点P作平行于x轴的直线,交直线
,过点P作平行于x轴的直线,交直线![]() 于点C,过点P作平行于y轴的直线交反比例函数
于点C,过点P作平行于y轴的直线交反比例函数![]() 的图象于点D,当
的图象于点D,当![]() 时,结合函数的图象,求出n的值.
时,结合函数的图象,求出n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】欧几里得在《几何原本》中,记载了用图解法解方程![]() 的方法,类似地我们可以用折纸的方法求方程
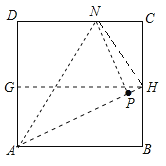
的方法,类似地我们可以用折纸的方法求方程![]() 的一个正根.如图,一张边长为1的正方形的纸片
的一个正根.如图,一张边长为1的正方形的纸片![]() ,先折出
,先折出![]() 、
、![]() 的中点
的中点![]() 、
、![]() ,再折出线段
,再折出线段![]() ,然后通过沿线段
,然后通过沿线段![]() 折叠使
折叠使![]() 落在线段
落在线段![]() 上,得到点
上,得到点![]() 的新位置
的新位置![]() ,并连接
,并连接![]() 、
、![]() ,此时,在下列四个选项中,有一条线段的长度恰好是方程
,此时,在下列四个选项中,有一条线段的长度恰好是方程![]() 的一个正根,则这条线段是( )
的一个正根,则这条线段是( )
A.线段![]() B.线段
B.线段![]() C.线段
C.线段![]() D.线段
D.线段![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年中国北京世界园艺博览会(以下简称“世园会”)于4月29日至10月7日在北京延庆区举行.世园会为满足大家的游览需求,倾情打造了![]() 条各具特色的趣玩路线,分别是:
条各具特色的趣玩路线,分别是:![]() .“解密世园会”、
.“解密世园会”、![]() .“爱我家, 爱园艺”、
.“爱我家, 爱园艺”、![]() .“园艺小清新之旅”、
.“园艺小清新之旅”、![]() .“快速车览之旅”.李明和张春各自在这
.“快速车览之旅”.李明和张春各自在这![]() 条线路中任意选择一条线路游览,每条线路被选择的可能性相同.
条线路中任意选择一条线路游览,每条线路被选择的可能性相同.
(1)李明选择线路![]() .“ 爱我家,爱园艺”的概率为 ;
.“ 爱我家,爱园艺”的概率为 ;
(2)用画树状图或列表的方法,求李明和张春恰好选择同一线路游览的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自从开展“创建全国文明城区“工作以来,门头沟区便掀起了“门头沟热心人“志愿服务的热潮,区教委也号召各校学生积极参与到志愿服务当中.为了解甲、乙两所学校学生一周志愿服务情况,从这两所学校中各随机抽取40名学生,分别对他们一周的志愿服务时长(单位:分钟)数据进行收集、整理、描述和分析.下面给出了部分信息:
a.甲校40名学生一周的志愿服务时长的扇形统计图如图(数据分成6组:![]() ):
):
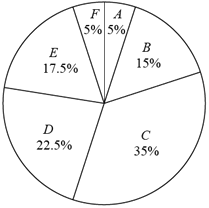
A:![]() B:
B:![]()
C:![]() D:
D:![]()
E:![]() F:
F:![]()
b.甲校40名学生一周志愿服务时长在![]() 这一组的是:
这一组的是:
60 60 62 63 65 68 70 72 73 75 75 76 80 80
c.甲、乙两校各抽取的40名学生一周志愿服务时长的平均数、中位数、众数如下:
学校 | 平均数 | 中位数 | 众数 |
甲校 | 75 |
| 90 |
乙校 | 75 | 76 | 85 |
根据以上信息,回答下列问题:
(1)![]() _____________;
_____________;
(2)根据上面的统计结果,你认为____①_____所学校学生志愿服务工作做得好(填“甲“或“乙“),理由______②________________________________________________________;
(3)甲校要求学生一周志愿服务的时长不少于60分钟,如果甲校共有学生800人,请估计甲校学生中一周志愿服务时长符合要求的有_______人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新型冠状肺炎给人类带来了灾难.口罩是抗击新冠肺炎的重要战略物资,国家在必要时进行价格限制,以保持价格稳定.某公司生产的口罩售价与天数的函数关系如图所示(曲线部分是以![]() 轴为对称轴的抛物线一部分).
轴为对称轴的抛物线一部分).
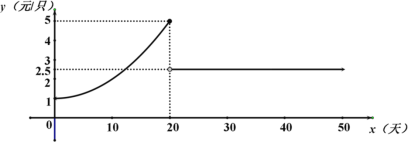
(1)求口罩销售价格![]() (元)与天数
(元)与天数![]() (天)之间的函数关系式;
(天)之间的函数关系式;
(2)若这种口罩每只成本![]() (元)与天数
(元)与天数![]() 之间的关系为:
之间的关系为: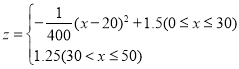 .那么这种口罩在第几天售出后单只利润最大?最大利润为多少?
.那么这种口罩在第几天售出后单只利润最大?最大利润为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
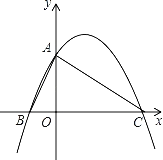
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与y轴交于点A(0,4),与x轴负半轴交于B,与正半轴交于点C(8,0),且∠BAC=90°.
(1)求该二次函数解析式;
(2)若N是线段BC上一动点,作NE∥AC,交AB于点E,连结AN,当△ANE面积最大时,求点N的坐标;
(3)若点P为x轴上方的抛物线上的一个动点,连接PA、PC,设所得△PAC的面积为S.问:是否存在一个S的值,使得相应的点P有且只有2个?若有,求出这个S的值,并求此时点P的横坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究:如图1和2,四边形![]() 中,已知
中,已知![]() ,
,![]() ,点
,点![]() ,
,![]() 分别在
分别在![]() 、
、![]() 上,
上,![]() .
.
(1)①如图 1,若![]() 、
、![]() 都是直角,把
都是直角,把![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 至
至![]() ,使
,使![]() 与
与![]() 重合,则能证得
重合,则能证得![]() ,请写出推理过程;
,请写出推理过程;
②如图 2,若![]() 、
、![]() 都不是直角,则当
都不是直角,则当![]() 与
与![]() 满足数量关系_______时,仍有
满足数量关系_______时,仍有![]() ;
;
(2)拓展:如图3,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 、
、![]() 均在边
均在边![]() 上,且
上,且![]() .若
.若![]() ,求
,求![]() 的长.
的长.
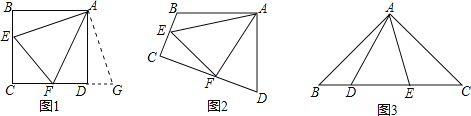
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索应用
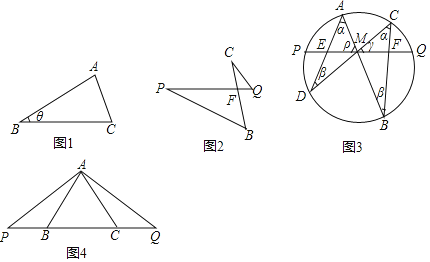
材料一:如图1,在△ABC中,AB=c,BC=a,∠B=θ,用c和θ表示BC边上的高为 ,用a.c和θ表示△ABC的面积为 .
材料二:如图2,已知∠C=∠P,求证:CFBF=QFPF.
材料三:蝴蝶定理(ButterflyTheorem)是古代欧氏平面几何中最精彩的结果之一,最早出现在1815年,由W.G.霍纳提出证明,定理的图形象一只蝴蝶.
定理:如图3,M为弦PQ的中点,过M作弦AB和CD,连结AD和BC交PQ分别于点E和F,则ME=MF.
证明:设∠A=∠C=α,∠B=∠D=β,
∠DMP=∠CMQ=γ,∠AMP=∠BMQ=ρ,
PM=MQ=a,ME=x,MF=y
由![]()
即![]()
化简得:MF2AEED=ME2CFFB
则有:![]() ,
,
又∵CFFB=QFFP,AEED=PEEQ,
∴![]() ,即
,即![]()
即![]() ,从而x=y,ME=MF.
,从而x=y,ME=MF.
请运用蝴蝶定理的证明方法解决下面的问题:
如图4,B、C为线段PQ上的两点,且BP=CQ,A为PQ外一动点,且满足∠BAP=∠CAQ,判断△PAQ的形状,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com