
ЁОЬтФПЁПЬНЫїгІгУ
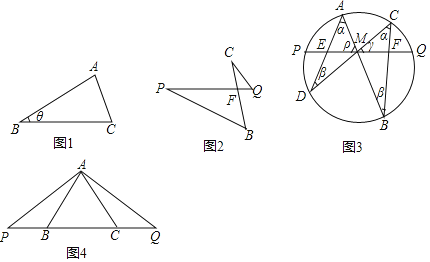
ВФСЯвЛЃКШчЭМ1ЃЌдкЁїABCжаЃЌABЃНcЃЌBCЃНaЃЌЁЯBЃНІШЃЌгУcКЭІШБэЪОBCБпЩЯЕФИпЮЊЁЁ ЁЁЃЌгУaЃЎcКЭІШБэЪОЁїABCЕФУцЛ§ЮЊЁЁ ЁЁЃЎ
ВФСЯЖўЃКШчЭМ2ЃЌвбжЊЁЯCЃНЁЯPЃЌЧѓжЄЃКCFBFЃНQFPFЃЎ
ВФСЯШ§ЃККћЕћЖЈРэЃЈButterflyTheoremЃЉЪЧЙХДњХЗЪЯЦНУцМИКЮжазюОЋВЪЕФНсЙћжЎвЛЃЌзюдчГіЯждк1815ФъЃЌгЩWЃЎGЃЎЛєФЩЬсГіжЄУїЃЌЖЈРэЕФЭМаЮЯѓвЛжЛКћЕћЃЎ
ЖЈРэЃКШчЭМ3ЃЌMЮЊЯвPQЕФжаЕуЃЌЙ§MзїЯвABКЭCDЃЌСЌНсADКЭBCНЛPQЗжБ№гкЕуEКЭFЃЌдђMEЃНMFЃЎ
жЄУїЃКЩшЁЯAЃНЁЯCЃНІСЃЌЁЯBЃНЁЯDЃНІТЃЌ
ЁЯDMPЃНЁЯCMQЃНІУЃЌЁЯAMPЃНЁЯBMQЃНІбЃЌ
PMЃНMQЃНaЃЌMEЃНxЃЌMFЃНy
гЩ![]()
МД![]()
ЛЏМђЕУЃКMF2AEEDЃНME2CFFB
дђгаЃК![]() ,
,
гжЁпCFFBЃНQFFPЃЌAEEDЃНPEEQЃЌ
Ёр![]() ЃЌМД
ЃЌМД![]()
МД![]() ЃЌДгЖјxЃНyЃЌMEЃНMFЃЎ
ЃЌДгЖјxЃНyЃЌMEЃНMFЃЎ
ЧыдЫгУКћЕћЖЈРэЕФжЄУїЗНЗЈНтОіЯТУцЕФЮЪЬтЃК
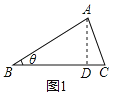
ШчЭМ4ЃЌBЁЂCЮЊЯпЖЮPQЩЯЕФСНЕуЃЌЧвBPЃНCQЃЌAЮЊPQЭтвЛЖЏЕуЃЌЧвТњзуЁЯBAPЃНЁЯCAQЃЌХаЖЯЁїPAQЕФаЮзДЃЌВЂжЄУїФуЕФНсТлЃЎ
ЁОД№АИЁПВФСЯвЛЃК![]() ЃЛВФСЯЖўЃКжЄУїМћНтЮіЃЛВФСЯШ§ЃКЁїPAQЕФаЮзДЮЊЕШбќШ§НЧаЮЃЌжЄУїМћНтЮіЃЎ
ЃЛВФСЯЖўЃКжЄУїМћНтЮіЃЛВФСЯШ§ЃКЁїPAQЕФаЮзДЮЊЕШбќШ§НЧаЮЃЌжЄУїМћНтЮіЃЎ
ЁОНтЮіЁП
ВФСЯвЛЃКзїADЁЭBCгкDЃЌгЩШ§НЧКЏЪ§ЖЈвхЕУADЃНABЁСsinBЃНcsinІШЃЌгЩШ§НЧаЮУцЛ§ЙЋЪНЕУЁїABCЕФУцЛ§ЃН![]() BCЁСADЃН
BCЁСADЃН![]() acsinІШМДПЩЃЛ
acsinІШМДПЩЃЛ
ВФСЯЖўЃКжЄУїЁїCFQЁзЁїPFBЃЌЕУГі![]() ЃН
ЃН![]() ЃЌМДПЩЕУГіНсТлЃЛ
ЃЌМДПЩЕУГіНсТлЃЛ
ВФСЯШ§ЃКжЄSЁїABPЃНSЁїACQЃЌSЁїAPCЃНSЁїAQBЃЌжЄЁїABPЁзЁїACQЃЌгЩSЁїABPЃНSЁїACQЃЌжЄГіAPЃНAQЃЌМДПЩЕУГіНсТлЃЎ
ВФСЯвЛЃК
НтЃКзїADЁЭBCгкDЃЌШчЭМ1ЫљЪОЃК
дђsinBЃН![]() ЃЌ
ЃЌ
ЁрADЃНABЁСsinBЃНcsinІШЃЌ
ЁрЁїABCЕФУцЛ§ЃН![]() BCЁСADЃН
BCЁСADЃН![]() acsinІШЃЌ
acsinІШЃЌ
ЙЪД№АИЮЊЃКcsinІШЃЌ![]() acsinІШЃЛ
acsinІШЃЛ
ВФСЯЖўЃК
жЄУїЃКЁпЁЯCЃНЁЯPЃЌЁЯCFQЃНЁЯPFBЃЌ
ЁрЁїCFQЁзЁїPFBЃЌ
Ёр![]() ЃН
ЃН![]() ,
,
ЁрCFBFЃНQFPFЃЛ
ВФСЯШ§ЃК
НтЃКЁїPAQЕФаЮзДЮЊЕШбќШ§НЧаЮЃЌРэгЩШчЯТЃК
ЁпBЁЂCЮЊЯпЖЮPQЩЯЕФСНЕуЃЌЧвBPЃНCQЃЌ
ЁрCPЃНBQЃЌ
ЁрЁїABPгыЁїACQЕШЕзЕШИпЃЌЁїAPCгыЁїAQBЕШЕзЕШИпЃЌ
ЁрSЁїABPЃНSЁїACQЃЌSЁїAPCЃНSЁїAQBЃЌ
ЁпЁЯBAPЃНЁЯCAQЃЌ
ЁрЁЯBAP+ЁЯBACЃНЁЯCAQ+ЁЯBACЃЌ
МДЁЯPACЃНЁЯQABЃЌ
ЁрsinЁЯQABЃНPsinЁЯPACЃЌ
ЁпSЁїAQBЃН![]() ABAQsinЁЯQABЃЌSЁїAPCЃН
ABAQsinЁЯQABЃЌSЁїAPCЃН![]() ACAPsinЁЯPACЃЌ
ACAPsinЁЯPACЃЌ
Ёр =
=![]() =1,
=1,
Ёр![]() =
=![]() ЃЌ
ЃЌ
ЁрЁїABPЁзЁїACQЃЌ
ЁпSЁїABPЃНSЁїACQЃЌ
Ёр![]() =
=![]() ЃН1ЃЌ
ЃН1ЃЌ
ЁрAPЃНAQЃЌ
ЁрЁїPAQЕФаЮзДЮЊЕШбќШ§НЧаЮЃЎ


 ЪРМЭАйЭЈЦкФЉН№ОэЯЕСаД№АИ
ЪРМЭАйЭЈЦкФЉН№ОэЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМе§ЗНаЮ![]() ЯШЯђгвЦНвЦ1ИіЕЅЮЛГЄЖШЃЌдйЯђЩЯЦНвЦ1ИіЕЅЮЛГЄЖШЃЌЕУЕНе§ЗНаЮ
ЯШЯђгвЦНвЦ1ИіЕЅЮЛГЄЖШЃЌдйЯђЩЯЦНвЦ1ИіЕЅЮЛГЄЖШЃЌЕУЕНе§ЗНаЮ![]() ЃЌаЮГЩСЫжаМфЩюЩЋЕФе§ЗНаЮМАЫФжмЧГЩЋЕФБпПђЃЌвбжЊе§ЗНаЮ
ЃЌаЮГЩСЫжаМфЩюЩЋЕФе§ЗНаЮМАЫФжмЧГЩЋЕФБпПђЃЌвбжЊе§ЗНаЮ![]() ЕФУцЛ§ЮЊ16ЃЌдђЫФжмЧГЩЋБпПђЕФУцЛ§ЪЧ________ЃЎ
ЕФУцЛ§ЮЊ16ЃЌдђЫФжмЧГЩЋБпПђЕФУцЛ§ЪЧ________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
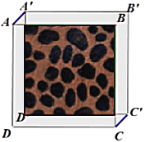
ЁОЬтФПЁПШчЭМЃЌABЪЧЁбOЕФжБОЖЃЌ OEДЙжБгкЯвBCЃЌДЙзуЮЊFЃЌOEНЛЁбOгкЕуDЃЌЧвЁЯCBE=2ЁЯCЃЎ
ЃЈ1ЃЉЧѓжЄЃКBEгыЁбOЯрЧаЃЛ
ЃЈ2ЃЉШєDF=9ЃЌtanC=![]() ЃЌЧѓжБОЖABЕФГЄЃЎ
ЃЌЧѓжБОЖABЕФГЄЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌвдЕу
ЃЌвдЕу![]() ЮЊдВаФЃЌ6ЮЊАыОЖЕФдВЩЯгавЛИіЖЏЕу
ЮЊдВаФЃЌ6ЮЊАыОЖЕФдВЩЯгавЛИіЖЏЕу![]() ЃЎСЌНг
ЃЎСЌНг![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЃЌдђ
ЃЌдђ![]() ЕФзюаЁжЕЪЧ_________ЃЎ
ЕФзюаЁжЕЪЧ_________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
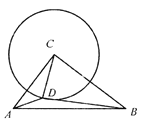
ЁОЬтФПЁПШчЭМЃЌЗжБ№вдЁїABCЕФБпABЁЂACЮЊвЛБпЯђЭтзіе§ЗНаЮABDEКЭе§ЗНаЮACFGЃЌСЌНсCEЁЂBGНЛгкЕуPЃЌСЌНсAPКЭEGЃЎдкВЛЬэМгШЮКЮИЈжњЯпКЭзжФИЕФЧАЬсЯТЃЌаДГіЫФИіВЛЭЌРраЭЕФНсТл_____ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
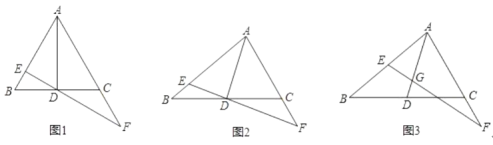
ЁОЬтФПЁП![]() жаЃЌ
жаЃЌ![]() ЪЧ
ЪЧ![]() ЕФжаЕуЃЌЕу
ЕФжаЕуЃЌЕу![]() дк
дк![]() ЩЯЃЈЕу
ЩЯЃЈЕу![]() ВЛгы
ВЛгы![]() жиКЯЃЉЃЌЙ§Еу
жиКЯЃЉЃЌЙ§Еу![]() ЕФжБЯпНЛ
ЕФжБЯпНЛ![]() гк
гк![]() ЃЌНЛЩфЯп
ЃЌНЛЩфЯп![]() гкЕу
гкЕу![]() ЃЌЩш
ЃЌЩш![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉШчЭМ1ЃЌШє![]() ЮЊЕШБпШ§НЧаЮЃЌЕу
ЮЊЕШБпШ§НЧаЮЃЌЕу![]() гы
гы![]() жиКЯЃЌ
жиКЯЃЌ![]() ЃЌЧѓжЄЃК
ЃЌЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌШєЕу![]() гы
гы![]() жиКЯЃЌЧѓжЄЃК
жиКЯЃЌЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ3ЃЉШчЭМ3ЃЌШє![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌжБНгаДГі
ЃЌжБНгаДГі![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌбгГЄ
ЃЌбгГЄ![]() ЪЙ
ЪЙ![]() ЃЌЯпЖЮ
ЃЌЯпЖЮ![]() ШЦЕуCЫГЪБеыа§зЊ90ЁуЕУЕНЯпЖЮ
ШЦЕуCЫГЪБеыа§зЊ90ЁуЕУЕНЯпЖЮ![]() ЃЌСЌНс
ЃЌСЌНс![]() ЃЎ
ЃЎ
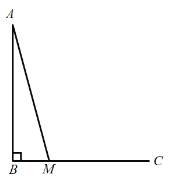
ЃЈ1ЃЉвРОнЬтвтВЙШЋЭМаЮЃЛ
ЃЈ2ЃЉЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЕФЖШЪ§ЪЧ__________ЃЛ
ЕФЖШЪ§ЪЧ__________ЃЛ
ЃЈ3ЃЉаЁДЯЭЈЙ§ЛЭМЁЂВтСПЗЂЯжЃЌЕБ![]() ЪЧвЛЖЈЖШЪ§ЪБЃЌ
ЪЧвЛЖЈЖШЪ§ЪБЃЌ![]() ЃЎ
ЃЎ
аЁДЯАбетИіВТЯыКЭЭЌбЇУЧНјааНЛСїЃЌЭЈЙ§ЬжТлЃЌаЮГЩСЫжЄУїИУВТЯыЕФМИжжЯыЗЈЃК
ЯыЗЈ1ЃКЭЈЙ§ЙлВьЭМаЮПЩвдЗЂЯжЃЌШчЙћАбЬнаЮ![]() ВЙШЋГЩЮЊе§ЗНаЮ
ВЙШЋГЩЮЊе§ЗНаЮ![]() ЃЌОЭвзжЄ
ЃЌОЭвзжЄ![]() ЃЌвђДЫвзЕУЕБ
ЃЌвђДЫвзЕУЕБ![]() ЪЧЬиЪтжЕЪБЃЌЮЪЬтЕУжЄЃЛ
ЪЧЬиЪтжЕЪБЃЌЮЪЬтЕУжЄЃЛ
ЯыЗЈ2ЃКвЊжЄ![]() ЃЌЭЈЙ§ЕкЃЈ2ЃЉЮЪЃЌПЩжЊжЛашвЊжЄУї
ЃЌЭЈЙ§ЕкЃЈ2ЃЉЮЪЃЌПЩжЊжЛашвЊжЄУї![]() ЪЧЕШБпШ§НЧаЮЃЌЭЈЙ§ЙЙдьЦНааЫФБпаЮ
ЪЧЕШБпШ§НЧаЮЃЌЭЈЙ§ЙЙдьЦНааЫФБпаЮ![]() ЃЌвзжЄ
ЃЌвзжЄ![]() ЃЌЭЈЙ§
ЃЌЭЈЙ§![]() ЃЌвзжЄ
ЃЌвзжЄ![]() ЃЌДгЖјНтОіЮЪЬтЃЛ
ЃЌДгЖјНтОіЮЪЬтЃЛ
ЯыЗЈ3ЃКЭЈЙ§![]() ЃЌСЌНс
ЃЌСЌНс![]() ЃЌвзжЄ
ЃЌвзжЄ![]() ЃЌвзЕУ
ЃЌвзЕУ![]() ЪЧЕШбќШ§НЧаЮЃЌвђДЫЕБ
ЪЧЕШбќШ§НЧаЮЃЌвђДЫЕБ![]() ЪЧЬиЪтжЕЪБЃЌЮЪЬтЕУжЄЃЎ
ЪЧЬиЪтжЕЪБЃЌЮЪЬтЕУжЄЃЎ
ЧыФуВЮПМЩЯУцЕФЯыЗЈЃЌАяжњаЁДЯжЄУїЕБ![]() ЪЧвЛЖЈЖШЪ§ЪБЃЌ
ЪЧвЛЖЈЖШЪ§ЪБЃЌ![]() ЃЎЃЈвЛжжЗНЗЈМДПЩЃЉ
ЃЎЃЈвЛжжЗНЗЈМДПЩЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП2020ФъаТЙкЗЮбзвпЧщЗЂЩњвдРДЃЌЮвЪаЙуДѓдкжАЕГдБЛ§МЋВЮгыЩчЧјЗРвпЙЄзїЃЌжњСІЩчЧјМсОіДђгЎвпЧщЗРПизшЛїеН.ЦфжаЃЌAЩчЧјга500УћдкжАЕГдБЃЌЮЊСЫНтБОЩчЧј2дТЁЊ3дТЦкМфдкжАЕГдБВЮМггІМБжДЧкЕФЧщПіЃЌAЩчЧјеыЖджДЧкЕФДЮЪ§ЫцЛњГщШЁ50УћдкжАЕГдБНјааЕїВщЃЌВЂЖдЪ§ОнНјааСЫећРэЁЂУшЪіКЭЗжЮіЃЌЯТУцИјГіСЫВПЗжаХЯЂЃЎ
ДЮЪ§x/ДЮ | ЦЕЪ§ | ЦЕТЪ |
0 Ёмx< 10 | 8 | 0.16 |
10Ёмx< 20 | 10 | 0.20 |
20Ёмx< 30 | 16 | b |
30Ёмx< 40 | a | 0.24 |
xЁн 40 | 4 | 0.08 |

ЦфжаЃЌгІМБжДЧкДЮЪ§дк20Ёмx< 30етвЛзщЕФЪ§ОнЪЧЃК
20 20 21 22 23 23 23 23 25 26 26 26 27 28 28 29
ЧыИљОнЫљИјаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉ![]() =ЁЁЁЁЁЁЁЁЁЁЁЁЃЌ
=ЁЁЁЁЁЁЁЁЁЁЁЁЃЌ![]() =ЁЁЁЁЁЁЁЁЁЁЁЁЃЛ
=ЁЁЁЁЁЁЁЁЁЁЁЁЃЛ
ЃЈ2ЃЉЧыВЙШЋЦЕЪ§ЗжВМжБЗНЭМЃЛ
ЃЈ3ЃЉЫцЛњГщШЁЕФ50УћдкжАЕГдБВЮМггІМБжДЧкДЮЪ§ЕФжаЮЛЪ§ЪЧЁЁЁЁЁЁЁЁЁЁЁЁЃЛ
ЃЈ4ЃЉЧыЙРМЦ2дТЁЊ3дТЦкМфAЩчЧјдкжАЕГдБВЮМггІМБжДЧкЕФДЮЪ§ВЛЕЭгк30ДЮЕФдМга__ШЫЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдквЛИіВЛЭИУїЕФКазгжазАга6еХПЈЦЌЃЌ6еХПЈЦЌЕФе§УцЗжБ№БъгаЪ§зжЉ4ЃЌЉ3ЃЌЉ2ЃЌЉ1ЃЌ6ЃЌ8ЃЌетаЉПЈЦЌГ§Ъ§зжЭтЖМЯрЭЌЃЌНЋПЈЦЌНСдШЃЎ
ЃЈ1ЃЉДгКазгжаШЮвтГщШЁвЛеХПЈЦЌЃЌЧѓЧЁКУГщЕНБъгаХМЪ§ПЈЦЌЕФИХТЪЃЛ
ЃЈ2ЃЉЯШДгКазгжаШЮвтГщШЁвЛеХПЈЦЌЃЌАбЫќЩЯУцЕФЪ§зжзїЮЊвЛИіЕуЕФКсзјБъЃЌВЛЗХЛиЃЌдйДгКазгЪЃгрЕФПЈЦЌжаШЮвтГщШЁвЛеХПЈЦЌЃЌАбЫќЩЯУцЕФЪ§зжзїЮЊетИіЕуЕФзнзјБъЃЌЧѓГщШЁЕФЕуЧЁКУТфдкЕкЖўЯѓЯоЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com