
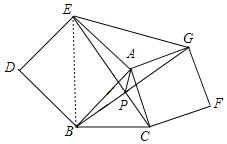
【题目】如图,分别以△ABC的边AB、AC为一边向外做正方形ABDE和正方形ACFG,连结CE、BG交于点P,连结AP和EG.在不添加任何辅助线和字母的前提下,写出四个不同类型的结论_____.

【答案】△AEC≌△ABG,EC=BG,EC⊥BG,AP平分∠EPG,
【解析】
如图,连接BE,由“SAS”可证△EAC≌△BAG,可得EC=BG,∠CEA=∠GBA,可证点P,点A,点E,点B四点共圆,可得∠EPB=∠EAB=90°,∠APE=∠ABE=45°,可得EC⊥BG,AP平分∠EPG.
解:△AEC≌△ABG,EC=BG,EC⊥BG,AP平分∠EPG,(答案不唯一)
理由如下:如图,连接BE,
∵正方形ABDE和正方形ACFG,
∴AB=AE,AC=AG,∠BAE=∠CAG=90°,∠ABE=45°
∴∠EAC=∠BAG,
∴△EAC≌△BAG(SAS),
∴EC=BG,∠CEA=∠GBA,
∵∠CEA=∠GBA,
∴点P,点A,点E,点B四点共圆,
∴∠EPB=∠EAB=90°,∠APE=∠ABE=45°,
∴EC⊥BG,∠EPG=90°,
∴∠APG=∠APE=45°,
∴AP平分∠EPG.


科目:初中数学 来源: 题型:
【题目】自从开展“创建全国文明城区“工作以来,门头沟区便掀起了“门头沟热心人“志愿服务的热潮,区教委也号召各校学生积极参与到志愿服务当中.为了解甲、乙两所学校学生一周志愿服务情况,从这两所学校中各随机抽取40名学生,分别对他们一周的志愿服务时长(单位:分钟)数据进行收集、整理、描述和分析.下面给出了部分信息:
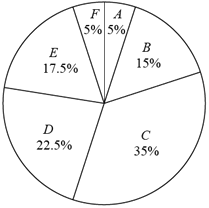
a.甲校40名学生一周的志愿服务时长的扇形统计图如图(数据分成6组:![]() ):
):
A:![]() B:
B:![]()
C:![]() D:
D:![]()
E:![]() F:
F:![]()
b.甲校40名学生一周志愿服务时长在![]() 这一组的是:
这一组的是:
60 60 62 63 65 68 70 72 73 75 75 76 80 80
c.甲、乙两校各抽取的40名学生一周志愿服务时长的平均数、中位数、众数如下:
学校 | 平均数 | 中位数 | 众数 |
甲校 | 75 |
| 90 |
乙校 | 75 | 76 | 85 |
根据以上信息,回答下列问题:
(1)![]() _____________;
_____________;
(2)根据上面的统计结果,你认为____①_____所学校学生志愿服务工作做得好(填“甲“或“乙“),理由______②________________________________________________________;
(3)甲校要求学生一周志愿服务的时长不少于60分钟,如果甲校共有学生800人,请估计甲校学生中一周志愿服务时长符合要求的有_______人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.为了解全国中学生视力的情况,应采用普查的方式
B.某种彩票中奖的概率是![]() ,买1000张这种彩票一定会中奖
,买1000张这种彩票一定会中奖
C.从2000名学生中随机抽取200名学生进行调查,样本容量为200名学生
D.从只装有白球和绿球的袋中任意摸出一个球,摸出黑球是确定事件
查看答案和解析>>
科目:初中数学 来源: 题型:
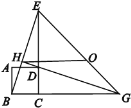
【题目】如图,四边形ABCD是正方形,ΔECG是等腰直角三角形,∠BGE的平分线过点D交BE 于H,O是EG的中点,对于下面四个结论:①GH⊥BE;②OH∥BG,且![]() ;③
;③![]() ;④△EBG的外接圆圆心和它的内切圆圆心都在直线HG上.其中表述正确的个数是( )
;④△EBG的外接圆圆心和它的内切圆圆心都在直线HG上.其中表述正确的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
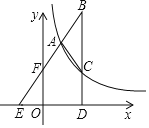
【题目】如图,在△ABC中,AB=AC,BC⊥x轴,垂足为D,边AB所在直线分别交x轴、y轴于点E、F,且AF=EF,反比例函数y=![]() 的图象经过A、C两点,已知点A(2,n).
的图象经过A、C两点,已知点A(2,n).
(1)求AB所在直线对应的函数表达式;(2)求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索应用
材料一:如图1,在△ABC中,AB=c,BC=a,∠B=θ,用c和θ表示BC边上的高为 ,用a.c和θ表示△ABC的面积为 .
材料二:如图2,已知∠C=∠P,求证:CFBF=QFPF.
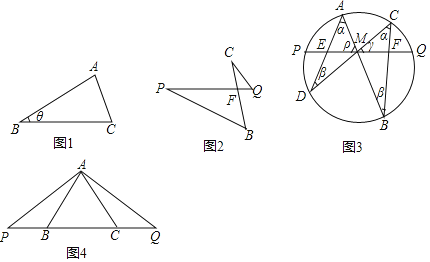
材料三:蝴蝶定理(ButterflyTheorem)是古代欧氏平面几何中最精彩的结果之一,最早出现在1815年,由W.G.霍纳提出证明,定理的图形象一只蝴蝶.
定理:如图3,M为弦PQ的中点,过M作弦AB和CD,连结AD和BC交PQ分别于点E和F,则ME=MF.
证明:设∠A=∠C=α,∠B=∠D=β,
∠DMP=∠CMQ=γ,∠AMP=∠BMQ=ρ,
PM=MQ=a,ME=x,MF=y
由![]()
即![]()
化简得:MF2AEED=ME2CFFB
则有:![]() ,
,
又∵CFFB=QFFP,AEED=PEEQ,
∴![]() ,即
,即![]()
即![]() ,从而x=y,ME=MF.
,从而x=y,ME=MF.
请运用蝴蝶定理的证明方法解决下面的问题:
如图4,B、C为线段PQ上的两点,且BP=CQ,A为PQ外一动点,且满足∠BAP=∠CAQ,判断△PAQ的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是某企业甲、乙两位员工的能力测试结果的网状图,以O为圆心的五个同心圆分别代表能力水平的五个等级由低到高分别赋分1至5分,由原点出发的五条线段分别指向能力水平的五个维度,网状图能够更加直观的描述测试者的优势和不足,观察图形,有以下几个推断:
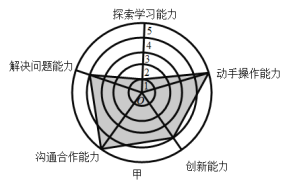
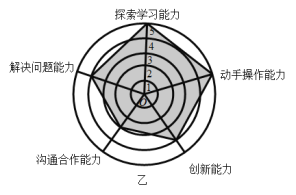
①甲和乙的动手操作能力都很强;
②缺少探索学习的能力是甲自身的不足;
③与甲相比乙需要加强与他人的沟通合作能力;
④乙的综合评分比甲要高.
其中合理的是( )
A.①③B.②④C.①②③D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C,D在⊙O上,弦AD的延长线与弦BC的延长线相交于点E.用①AB是⊙O的直径,②CB=CE,③AB=AE中的两个作为题设,余下的一个作为结论组成一个命题,则组成真命题的个数为( )
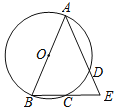
A.0B.1C.2D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.经过有交通信号灯的路口,遇到绿灯是必然事件
B.抛掷一枚均匀的硬币,10次都是正面朝上是随机事件
C.“明天下雨的概率是40%”就是说“明天有40%的时间都在下雨”
D.从装有3个红球和4个黑球的袋子里摸出一个球是红球的概率是![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com