
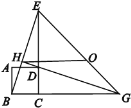
【题目】如图,四边形ABCD是正方形,ΔECG是等腰直角三角形,∠BGE的平分线过点D交BE 于H,O是EG的中点,对于下面四个结论:①GH⊥BE;②OH∥BG,且![]() ;③
;③![]() ;④△EBG的外接圆圆心和它的内切圆圆心都在直线HG上.其中表述正确的个数是( )
;④△EBG的外接圆圆心和它的内切圆圆心都在直线HG上.其中表述正确的个数是( )
A.1B.2C.3D.4
【答案】D
【解析】
①由四边形ABCD是正方形,△ECG是等腰直角三角形,得出△BCE≌△DCG,推出∠BEC+∠HDE=90°,从而得出GH⊥BE;
②由GH是∠EGC的平分线,得出△BGH≌△EGH,再由O是EG的中点,利用中位线定理,得出OH∥BG,且![]() ;
;
③由(2)得BG=EG,设CG=x,则CE=x,根据勾股定理得EG=![]() x,所以BG=
x,所以BG=![]() x,从而得到BC=(
x,从而得到BC=(![]() -1)x,根据正方形面积公式和等腰直角三角形面积公式可以得到S正方形ABCD=(3-2
-1)x,根据正方形面积公式和等腰直角三角形面积公式可以得到S正方形ABCD=(3-2![]() )x2,S△ECG=
)x2,S△ECG=![]() x2,进而求出
x2,进而求出![]() ;
;
④三角形的外接圆的圆心是三条边的垂直平分线的交点,三角形的内切圆是的圆心是三个角的平分线的交点.由(2)得BG=EG,由(1)得GH⊥BE,因为GH平分∠BGE,所以GH是BE边上的垂直平分线,所以△EBG的外接圆圆心和内切圆圆心在直线HG上.
解:①∵四边形ABCD是正方形,△ECG是等腰直角三角形
∴BC=CD,CE=CG,∠BCE=∠DCG=90°
在△BCE和△DCG中,
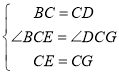
∴△BCE≌△DCG(SAS)
∴∠BEC=∠BGH
∵∠BGH+∠CDG=90°,∠CDG=∠HDE
∴∠BEC+∠HDE=90°
∴GH⊥BE
故①正确;
②∵GH是∠EGC的平分线
∴∠BGH=∠EGH
在△BGH和△EGH中,
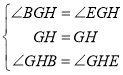
∴△BGH≌△EGH(ASA)
∴BH=EH
∵O是EG的中点
∴HO是△EBG的中位线
∴OH∥BG,且![]()
故②正确;
③由(2)得△BGH≌△EGH
∴BG=EG
在等腰直角三角形ECG中,设CG=x,则CE=x
∴EG=![]() =
=![]() x
x
∴BG=![]() x
x
∴BC=BG-CG=![]() x-x=(
x-x=(![]() -1)x
-1)x
∴S正方形ABCD=BC2=[(![]() -1)x]2 =(3-2
-1)x]2 =(3-2![]() )x2
)x2
S△ECG=![]()
![]() CG
CG![]() CE=
CE=![]() x2
x2
∴S正方形ABCD∶S△ECG=(3-2![]() )x2∶
)x2∶![]() x2=(6-4
x2=(6-4![]() )∶1
)∶1
故③正确;
④由(2)得BG=EG,由(1)得GH⊥BE
∵GH平分∠BGE,
∴GH是BE边上的垂直平分线
∵三角形的外接圆的圆心是三条边的垂直平分线的交点,三角形的内切圆是的圆心是三个角的平分线的交点.
∴△EBG的外接圆圆心和内切圆圆心在直线HG上
故④正确.
故选D.


 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,正方形![]() .... 按如图的方式放置.点
.... 按如图的方式放置.点![]()
![]() 和点
和点![]() 分别落在直线
分别落在直线![]() 和
和![]() 轴上.抛物线
轴上.抛物线![]() 过点
过点![]() ,且顶点在直线
,且顶点在直线![]() 上,抛物线
上,抛物线![]() 过点
过点![]() ,且顶点在直线
,且顶点在直线![]() 上,...按此规律,抛物线
上,...按此规律,抛物线![]() ,过点
,过点![]() , 且顶点也在直线
, 且顶点也在直线![]() 上,其中抛物线
上,其中抛物线![]() 交正方形
交正方形![]() 的边
的边![]() 于点
于点![]() ,抛物线
,抛物线![]() 交正方形
交正方形![]() 的边
的边![]() 于点
于点![]() (其中
(其中![]() 且
且![]() 为正整数) .
为正整数) .

(1)直接写出下列点的坐标:![]() ,
,![]() ;
;
(2)写出抛物线![]() 的解析式,并写出抛物线
的解析式,并写出抛物线![]() 的解析式求解过程,再猜想抛物线
的解析式求解过程,再猜想抛物线![]() 的顶点坐标;
的顶点坐标;
(3)设![]() ,试判断
,试判断![]() 与
与![]() 的数量关系并说明理由.
的数量关系并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在坐标系中放置一菱形OABC,已知∠ABC=60°,OA=1.先将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2020次,点B的落点依次为B1,B2,B3,…,则B2020的坐标为_________.
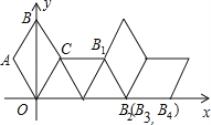
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径, OE垂直于弦BC,垂足为F,OE交⊙O于点D,且∠CBE=2∠C.
(1)求证:BE与⊙O相切;
(2)若DF=9,tanC=![]() ,求直径AB的长.
,求直径AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
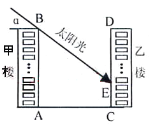
【题目】下图为某小区的两幢1O层住宅楼,由地面向上依次为第1层、第2层、…、第10层,每层的高度为3m,两楼间的距离AC=30m.现需了解在某一时段内,甲楼对乙楼的采光的影响情况.假设某一时刻甲楼楼顶B落在乙楼的影子长EC=h,太阳光线与水平线的夹角为α.
(1)用含α的式子表示h;
(2)当α=30°时,甲楼楼顶B的影子落在乙楼的第几层?从此时算起,若α每小时增加10°,几小时后,甲楼的影子刚好不影响乙楼采光.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别以△ABC的边AB、AC为一边向外做正方形ABDE和正方形ACFG,连结CE、BG交于点P,连结AP和EG.在不添加任何辅助线和字母的前提下,写出四个不同类型的结论_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,延长
,延长![]() 使
使![]() ,线段
,线段![]() 绕点C顺时针旋转90°得到线段
绕点C顺时针旋转90°得到线段![]() ,连结
,连结![]() .
.
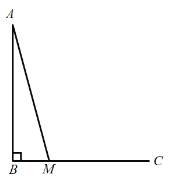
(1)依据题意补全图形;
(2)当![]() 时,
时,![]() 的度数是__________;
的度数是__________;
(3)小聪通过画图、测量发现,当![]() 是一定度数时,
是一定度数时,![]() .
.
小聪把这个猜想和同学们进行交流,通过讨论,形成了证明该猜想的几种想法:
想法1:通过观察图形可以发现,如果把梯形![]() 补全成为正方形
补全成为正方形![]() ,就易证
,就易证![]() ,因此易得当
,因此易得当![]() 是特殊值时,问题得证;
是特殊值时,问题得证;
想法2:要证![]() ,通过第(2)问,可知只需要证明
,通过第(2)问,可知只需要证明![]() 是等边三角形,通过构造平行四边形
是等边三角形,通过构造平行四边形![]() ,易证
,易证![]() ,通过
,通过![]() ,易证
,易证![]() ,从而解决问题;
,从而解决问题;
想法3:通过![]() ,连结
,连结![]() ,易证
,易证![]() ,易得
,易得![]() 是等腰三角形,因此当
是等腰三角形,因此当![]() 是特殊值时,问题得证.
是特殊值时,问题得证.
请你参考上面的想法,帮助小聪证明当![]() 是一定度数时,
是一定度数时,![]() .(一种方法即可)
.(一种方法即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
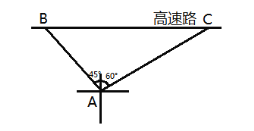
【题目】很多交通事故是由于超速行驶导致的,为集中治理超速现象,高速交警在距离高速路40米的地方设置了一个测速观察点,现测得测速点的西北方向有一辆小型轿车从B处沿西向正东方向行驶,2秒钟后到达测速点北偏东![]() 的方向上的C处,如图.
的方向上的C处,如图.
(1)求该小型轿车在测速过程中的平均行驶速度约是多少千米/时(精确到1千米/时)?
(参考数据:![]() )
)
(2)我国交通法规定:小轿车在高速路行驶,时速超过限定速度10%以上不到50%的处200元罚款,扣3分;时速超过限定速度50%以上不到70%的处1500元罚款,扣12分;时速超过限定时速70%以上的处1500元罚款,扣12分.若该高速路段限速120千米/时,你认为该小轿车驾驶员会受到怎样的处罚.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com