
【题目】在一个不透明的盒子中装有6张卡片,6张卡片的正面分别标有数字﹣4,﹣3,﹣2,﹣1,6,8,这些卡片除数字外都相同,将卡片搅匀.
(1)从盒子中任意抽取一张卡片,求恰好抽到标有偶数卡片的概率;
(2)先从盒子中任意抽取一张卡片,把它上面的数字作为一个点的横坐标,不放回,再从盒子剩余的卡片中任意抽取一张卡片,把它上面的数字作为这个点的纵坐标,求抽取的点恰好落在第二象限的概率.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)直接利用概率公式计算可得;
(2)列表得出所有等可能结果,从中找到符合条件的结果数,再根据概率公式计算可得.
(1)6张卡片中,偶数卡片有-4,-2, 6,8共4张,
∴恰好抽到标有偶数卡片的概率为![]() ;
;
(2)列表如下:
-4 | -3 | -2 | -1 | 6 | 8 | |
-4 | (-3,-4) | (-2,-4) | (-1,-4) | (6,-4) | (8,-4) | |
-3 | (-4,-3) | (-2,-3) | (-1,-3) | (6,-3) | (8,-3) | |
-2 | (-4,-2) | (-3,-2) | (-1,-2) | (6,-2) | (8,-2) | |
-1 | (-4,-1) | (-3,-1) | (-2,-1) | (6,-1) | (8,-1) | |
6 | (-4,6) | (-3,6) | (-2,6) | (-1,6) | (8,6) | |
8 | (-4,8) | (-3,8) | (-2,8) | (-1,8) | (6,8) |
由表可知共有30种等可能结果,其中落在第二象限的有8种结果,
∴抽取的点恰好落在第二象限的概率为![]() .
.


科目:初中数学 来源: 题型:
【题目】探索应用
材料一:如图1,在△ABC中,AB=c,BC=a,∠B=θ,用c和θ表示BC边上的高为 ,用a.c和θ表示△ABC的面积为 .
材料二:如图2,已知∠C=∠P,求证:CFBF=QFPF.
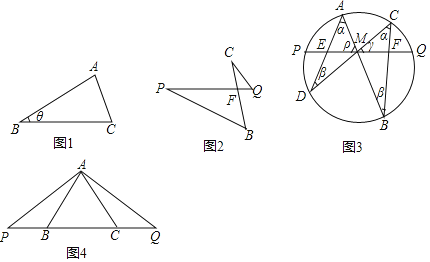
材料三:蝴蝶定理(ButterflyTheorem)是古代欧氏平面几何中最精彩的结果之一,最早出现在1815年,由W.G.霍纳提出证明,定理的图形象一只蝴蝶.
定理:如图3,M为弦PQ的中点,过M作弦AB和CD,连结AD和BC交PQ分别于点E和F,则ME=MF.
证明:设∠A=∠C=α,∠B=∠D=β,
∠DMP=∠CMQ=γ,∠AMP=∠BMQ=ρ,
PM=MQ=a,ME=x,MF=y
由![]()
即![]()
化简得:MF2AEED=ME2CFFB
则有:![]() ,
,
又∵CFFB=QFFP,AEED=PEEQ,
∴![]() ,即
,即![]()
即![]() ,从而x=y,ME=MF.
,从而x=y,ME=MF.
请运用蝴蝶定理的证明方法解决下面的问题:
如图4,B、C为线段PQ上的两点,且BP=CQ,A为PQ外一动点,且满足∠BAP=∠CAQ,判断△PAQ的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,以AB为直径的⊙O与BC相交于点D,与CA的延长线相交于点E,过点D作DF⊥AC于点F.

(1)试说明DF是⊙O的切线;
(2)若AC=3AE,求tanC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.经过有交通信号灯的路口,遇到绿灯是必然事件
B.抛掷一枚均匀的硬币,10次都是正面朝上是随机事件
C.“明天下雨的概率是40%”就是说“明天有40%的时间都在下雨”
D.从装有3个红球和4个黑球的袋子里摸出一个球是红球的概率是![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究
如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() ,点
,点![]() 为抛物线对称轴上一动点.
为抛物线对称轴上一动点.
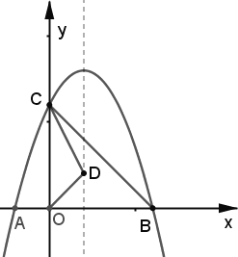
(1)求直线![]() 的函数表达式;
的函数表达式;
(2)连接![]() ,求
,求![]() 周长的最小值;
周长的最小值;
(3)在抛物线上是否存在一点![]() .使以
.使以![]() 为顶点的四边形是以
为顶点的四边形是以![]() 为边的平行四边形?若存在,请直接写出
为边的平行四边形?若存在,请直接写出![]() 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一次函数y=﹣x﹣6与x轴,y轴分别交于点A,B将直线AB沿y轴正方向平移与反比例函数y=![]() (x>0)的图象分别交于点C,D,连接BC交x轴于点E,连接AC,已知BE=3CE,且S△ABE=27.
(x>0)的图象分别交于点C,D,连接BC交x轴于点E,连接AC,已知BE=3CE,且S△ABE=27.
(1)求直线AC和反比例函数的解析式;
(2)连接AD,求△ACD的面积.
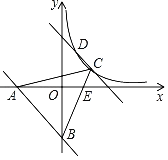
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l:y=x+1与y轴交于点A,与双曲线![]() (x>0)交于点B(2,a).
(x>0)交于点B(2,a).
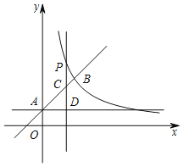
(1)求a,k的值.
(2)点P是直线l上方的双曲线上一点,过点P作平行于y轴的直线,交直线l于点C,过点A作平行于x轴的直线,交直线PC于点D,设点P的横坐标为m.
①若m=![]() ,试判断线段CP与CD的数量关系,并说明理由;②若CP>CD,请结合函数图象,直接写出m的取值范围.
,试判断线段CP与CD的数量关系,并说明理由;②若CP>CD,请结合函数图象,直接写出m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com