
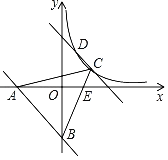
【题目】如图所示,一次函数y=﹣x﹣6与x轴,y轴分别交于点A,B将直线AB沿y轴正方向平移与反比例函数y=![]() (x>0)的图象分别交于点C,D,连接BC交x轴于点E,连接AC,已知BE=3CE,且S△ABE=27.
(x>0)的图象分别交于点C,D,连接BC交x轴于点E,连接AC,已知BE=3CE,且S△ABE=27.
(1)求直线AC和反比例函数的解析式;
(2)连接AD,求△ACD的面积.
【答案】(1)y=![]() ,y=
,y=![]() x+
x+![]() ;(2)12
;(2)12
【解析】
(1)先求得y=﹣x﹣6与坐标轴的交点,从而可得点A和点B的坐标,进而求得AE和OE的长;过C作CN⊥x轴于N,由平行线截线段成比例定理可得比例式,从而求得EN、CN和ON,则点C的坐标可得;从而反比例函数的解析式可得;设直线AC的解析式为y=kx+b(k≠0),用待定系数法即可求得答案;
(2)根据题意设直线CD的解析式为y=﹣x+b1,将点C(4,2)代入,解得b1的值,则CD的解析式可得;将直线CD和反比例函数解析式联立可解得点D的坐标;过D作DM∥y轴交AC于M,利用关系式S△ACD=S△ADM+S△CDM可求得答案.
解:(1)在y=﹣x﹣6中,当x=0时,y=﹣6;当y=0时,x=﹣6,
∴A(﹣6,0),B(0,﹣6),
∴OB=OA=6,又S△ABE=27,
∴![]() OB×AE=27,
OB×AE=27,
∴AE=9,OE=3,
过C作CN⊥x轴于N,

则CN∥OB,
又∵BE=3CE,
∴![]() ,
,
∴EN=1,CN=2,ON=4,
∴C(4,2),
∴反比例函数的解析式为y=![]() ,
,
设直线AC的解析式为y=kx+b(k≠0),将A(﹣6,0),C(4,2)代入得:
![]() ,
,
解得:![]() ,
,
∴直线AC的解析式为y=![]() x+
x+![]() ;
;
(2)根据题意设直线CD的解析式为y=﹣x+b1,将点C(4,2)代入得:
﹣4+b1=2,
∴b1=6,
∴直线CD的解析式为y=﹣x+6,
将直线CD和反比例函数解析式联立得: ,
,
解得: 或
或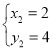 ,
,
∴D(2,4),
过D作DM∥y轴交AC于M,则M(2,1.6),

∴S△ACD=S△ADM+S△CDM
=![]() DM|xM﹣xA|+
DM|xM﹣xA|+![]() DM|xC﹣xM|
DM|xC﹣xM|
=![]() DM|xC﹣xA|
DM|xC﹣xA|
=![]() ×(4﹣1.6)×|4﹣(﹣6)|
×(4﹣1.6)×|4﹣(﹣6)|
=12.


科目:初中数学 来源: 题型:
【题目】2020年新冠肺炎疫情发生以来,我市广大在职党员积极参与社区防疫工作,助力社区坚决打赢疫情防控阻击战.其中,A社区有500名在职党员,为了解本社区2月—3月期间在职党员参加应急执勤的情况,A社区针对执勤的次数随机抽取50名在职党员进行调查,并对数据进行了整理、描述和分析,下面给出了部分信息.
次数x/次 | 频数 | 频率 |
0 ≤x< 10 | 8 | 0.16 |
10≤x< 20 | 10 | 0.20 |
20≤x< 30 | 16 | b |
30≤x< 40 | a | 0.24 |
x≥ 40 | 4 | 0.08 |

其中,应急执勤次数在20≤x< 30这一组的数据是:
20 20 21 22 23 23 23 23 25 26 26 26 27 28 28 29
请根据所给信息,解答下列问题:
(1)![]() = ,
= ,![]() = ;
= ;
(2)请补全频数分布直方图;
(3)随机抽取的50名在职党员参加应急执勤次数的中位数是 ;
(4)请估计2月—3月期间A社区在职党员参加应急执勤的次数不低于30次的约有__人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子中装有6张卡片,6张卡片的正面分别标有数字﹣4,﹣3,﹣2,﹣1,6,8,这些卡片除数字外都相同,将卡片搅匀.
(1)从盒子中任意抽取一张卡片,求恰好抽到标有偶数卡片的概率;
(2)先从盒子中任意抽取一张卡片,把它上面的数字作为一个点的横坐标,不放回,再从盒子剩余的卡片中任意抽取一张卡片,把它上面的数字作为这个点的纵坐标,求抽取的点恰好落在第二象限的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:小明为了计算![]() 的值 ,采用以下方法:
的值 ,采用以下方法:
设![]() ①
①
则![]() ②
②
②-①得 ![]()
∴![]()
(1)![]() = ;
= ;
(2)![]() = ;
= ;
(3)求![]() 的和(
的和(![]() ,
,![]() 是正整数,请写出计算过程 ).
是正整数,请写出计算过程 ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大邑县某汽车出租公司有若干辆同一型号的货车对外出租,每辆货车的日租金实行淡季、旺季两种价格标准,旺季每辆货车的日租金比淡季上涨25%.据统计,淡季该公司平均每天有10辆货车未出租,日租金总收入为3200元;旺季所有的货车每天能全部租出,日租金总收入为6000元.
(1)求该出租公司这批对外出租的货车共有多少辆?
(2)经市场调查发现,在旺季如果每辆货车的日租金每上涨20元,每天租出去的货车就会减少1辆,不考虑其它因素,该出租公司的日租金总收入最高是多少元?当日租金总收入最高时,每天出租货车多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有甲、乙两家草莓采摘园,草莓的销售价格相间,在生长旺季,两家均排出优惠方案.甲园的优惠方案是:采摘的草莓不超过![]() 时,按原价销售;若超过
时,按原价销售;若超过![]() 超过部分
超过部分![]() 折优惠;乙园的优惠方案是:游客进园需购买
折优惠;乙园的优惠方案是:游客进园需购买![]() 元门票.采摘的草莓直接按降价出售.已知在甲园、乙园采摘草莓
元门票.采摘的草莓直接按降价出售.已知在甲园、乙园采摘草莓![]() 时,所需费用相同.
时,所需费用相同.
在乙采摘园所需费用![]() ( 元)与草梅采摘量
( 元)与草梅采摘量![]() (千克)满足一次函数关系,如下表:
(千克)满足一次函数关系,如下表:
数量 |
|
|
|
| ··· |
费用 |
|
|
|
| ··· |
(1)求![]() 与
与![]() 的函数关系式(不必写出
的函数关系式(不必写出![]() 的范围);
的范围);
(2)求两个采摘园的草莓在生长旺季前的销售价格.并求在甲采摘园所需费用![]() (元)与草莓采摘量
(元)与草莓采摘量![]() (千克)的函数关系式
(千克)的函数关系式![]() ;
;
(3)若嘉琪准备花费![]() 元去采摘草莓,去哪个园采摘,可以得到更多数量的草莓? 说明理由.
元去采摘草莓,去哪个园采摘,可以得到更多数量的草莓? 说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了增强中学生的体质,某校食堂每天都为学生提供一定数量的水果,学校李老师为了了解学生喜欢吃哪种水果,进行了抽样调查,调查分为五种类型:A喜欢吃苹果的学生;B喜欢吃桔子的学生;C.喜欢吃梨的学生;D.喜欢吃香蕉的学生;E喜欢吃西瓜的学生,并将调查结果绘制成图1和图2 的统计图(不完整).请根据图中提供的数据解答下列问题:

(1)求此次抽查的学生人数;
(2)将图2补充完整,并求图1中的![]() ;
;
(3)现有5名学生,其中A类型2名,B类型2名,从中任选2名学生参加很体能测试,求这两名学生为同一类型的概率(用列表法或树状图法)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com