
科目: 来源: 题型:
【题目】如图,△ABC中,AB=![]() ,AC=5,tanA=2,D是BC中点,点P是AC上一个动点,将△BPD沿PD折叠,折叠后的三角形与△PBC的重合部分面积恰好等于△BPD面积的一半,则AP的长为______.
,AC=5,tanA=2,D是BC中点,点P是AC上一个动点,将△BPD沿PD折叠,折叠后的三角形与△PBC的重合部分面积恰好等于△BPD面积的一半,则AP的长为______.

查看答案和解析>>
科目: 来源: 题型:
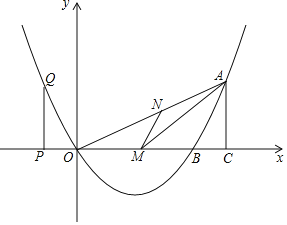
【题目】如图,已知二次函数的图象过点O(0,0).A(8,4),与x轴交于另一点B,且对称轴是直线x=3.
(1)求该二次函数的解析式;
(2)若M是OB上的一点,作MN∥AB交OA于N,当△ANM面积最大时,求M的坐标;
(3)P是x轴上的点,过P作PQ⊥x轴与抛物线交于Q.过A作AC⊥x轴于C,当以O,P,Q为顶点的三角形与以O,A,C为顶点的三角形相似时,求P点的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在⊙O中,AB为直径,AC为弦.过BC延长线上一点G,作GD⊥AO于点D,交AC于点E,交⊙O于点F,M是GE的中点,连接CF,CM.
(1)判断CM与⊙O的位置关系,并说明理由;
(2)若∠ECF=2∠A,CM=6,CF=4,求MF的长.

查看答案和解析>>
科目: 来源: 题型:
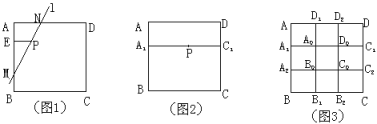
【题目】在一次课题学习中活动中,老师提出了如下一个问题:
点P是正方形ABCD内的一点,过点P画直线l分别交正方形的两边于点M、N,使点P是线段MN的三等分点,这样的直线能够画几条?
经过思考,甲同学给出如下画法:
如图1,过点P画PE⊥AB于E,在EB上取点M,使EM=2EA,画直线MP交AD于N,则直线MN就是符合条件的直线l.
根据以上信息,解决下列问题:
(1)甲同学的画法是否正确?请说明理由.
(2)在图1中,能否画出符合题目条件的直线?如果能,请直接在图1中画出.
(3)如图2,A1、C1分别是正方形ABCD的边AB、CD上的三等分点,且A1C1∥AD.当点P在线段A1C1上时,能否画出符合题目条件的直线?如果能,可以画出几条?
(4)如图3,正方形ABCD边界上的A1、A2、B1、B2、C1、C2、D1、D2都是所在边的三等分点.当点P在正方形ABCD内的不同位置时,试讨论,符合题目条件的直线l的条数的情况.
查看答案和解析>>
科目: 来源: 题型:
【题目】2013年某企业按餐厨垃圾处理费25元/吨,建筑垃圾处理费16元/吨标准,共支付餐厨和建筑垃圾处理费5200元,从2014年元月起,收费标准上调为:餐厨垃圾处理费100元/吨,建筑垃圾处理费30元/吨,若该企业2014年处理的这两种垃圾数量与2013年相比没有变化,就要多支付垃圾处理费8800元,
(1)该企业2013年处理的餐厨垃圾和建筑垃圾各多少吨?
(2)该企业计划2014年将上述两种垃圾处理量减少到240吨,且建筑垃圾处理费不超过餐厨垃圾处理量的3倍,则2014年该企业最少需要支付这两种垃圾处理费共多少元?
查看答案和解析>>
科目: 来源: 题型:
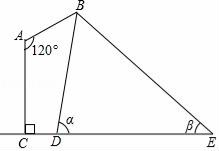
【题目】如图是某路灯在铅垂面内的示意图,灯柱AC的高为11米,灯杆AB与灯柱AC的夹角∠A=120°,路灯采用锥形灯罩,在地面上的照射区域DE长为18米,从D,E两处测得路灯B的仰角分别为α和β,且tanα=6,tanβ=![]() ,求灯杆AB的长度.
,求灯杆AB的长度.
查看答案和解析>>
科目: 来源: 题型:
【题目】为迎接十二运,某校开设了A:篮球,B:毽球,C:跳绳,D:健美操四种体育活动,为了解学生对这四种体育活动的喜欢情况,在全校范围内随机抽取若干名学生,进行问卷调查(每个被调查的同学必须选择而且只能在4中体育活动中选择一种).将数据进行整理并绘制成以下两幅统计图(未画完整).

(1)这次调查中,一共查了 名学生:
(2)请补全两幅统计图:
(3)若有3名最喜欢毽球运动的学生,1名最喜欢跳绳运动的学生组队外出参加一次联谊互活动,欲从中选出2人担任组长(不分正副),求两人均是最喜欢毽球运动的学生的概率.
查看答案和解析>>
科目: 来源: 题型:
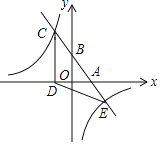
【题目】如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=![]() (n为常数,且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂足为D,若OB=2OA=3OD=12.
(n为常数,且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂足为D,若OB=2OA=3OD=12.
(1)求一次函数与反比例函数的解析式;
(2)记两函数图象的另一个交点为E,求△CDE的面积;
(3)直接写出不等式kx+b≤![]() 的解集.
的解集.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,若二次函数y=ax2+bx+c(a≠0)图象的对称轴为x=1,与y轴交于点C,与x轴交于点A、点B(﹣1,0),则
①二次函数的最大值为a+b+c;
②a﹣b+c<0;
③b2﹣4ac<0;
④当y>0时,﹣1<x<3,其中正确的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目: 来源: 题型:
【题目】在2016年泉州市初中体育中考中,随意抽取某校5位同学一分钟跳绳的次数分别为:158,160,154,158,170,则由这组数据得到的结论错误的是( )
A. 平均数为160 B. 中位数为158 C. 众数为158 D. 方差为20.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com