
科目: 来源: 题型:
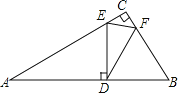
【题目】如图,在一块直角三角板ABC中,∠C=90°,∠A=30°,BC=1,将另一个含30°角的△EDF的30°角的顶点D放在AB边上,E、F分别在AC、BC上,当点D在AB边上移动时,DE始终与AB垂直,若△CEF与△DEF相似,则AD= .
查看答案和解析>>
科目: 来源: 题型:
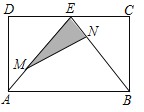
【题目】如图,在矩形ABCD中,AB = 8,AD = 4,E为CD的中点,连接AE、BE,点M从点A出发沿AE方向向点E匀速运动,同时点N从点E出发沿EB方向向点B匀速运动,点M、N运动速度均为每秒1个单位长度,运动时间为t,连接MN,设△EMN的面积为S,则S关于t的函数图像为( )
A. 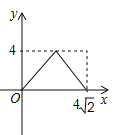 B.
B. 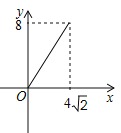
C. 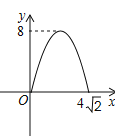 D.
D. 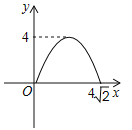
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,抛物线y=ax2+bx +3与x轴的交点为A和B,其中点A(-1,0),且点D(2,3)在该抛物线上.
(1)求该抛物线所对应的函数解析式;
(2)点P是线段AB上的动点(点P不与点A,B重合),过点P作PQ⊥x轴交该抛物线于点Q,连接AQ,DQ,记点P的横坐标为t.
①若![]() 时,求△
时,求△![]() 面积的最大值;
面积的最大值;
②若△![]() 是以Q为直角顶点的直角三角形时,求所有满足条件的点Q的坐标.
是以Q为直角顶点的直角三角形时,求所有满足条件的点Q的坐标.
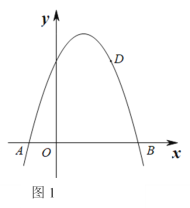
查看答案和解析>>
科目: 来源: 题型:
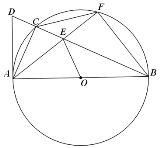
【题目】如图,△ABC是⊙O内接三角形,AB是⊙O的直径,C是弧AF的中点,弦BC,AF相交于点E,在BC延长线上取点D,使得AD=AE.
(1)求证:AD是⊙O切线;
(2)若∠OEB=45°,求sin∠ABD的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】新冠疫情初期,医用口罩是紧缺物资.某市为降低因购买口罩造成人群聚集的感染风险,通过APP实名预约,以摇号抽签的方式,由市民到指定门店购买口罩.规定:已中签者在本轮摇号结束前不再参与摇号;若指定门店当日市民购买口罩的平均等待时间超过8分钟,则次日必须增派工作人员.
(1)据APP数据统计:第一天有386.5万人进行网上预约,此后每天预约新增4万人,且每天有35.5万人中签,若小明第一天没有中签,则他第二天中签的概率是多少?
(2)该市某区指定A,B两门店每天8:00-22:00时段让中签市民排队购买口罩.图1是A门店某日购买口罩的人数与等待时间的统计图,为了算出A门店某日等待9分钟的人数,小红选择14:00~16:00这个时间段到店进行统计,统计结果见表1,且这个时间段的人数占该店当天等待9分钟人数的![]() .表2是B门店某日购买口罩的人数与等待时间的统计表.请你运用所学的统计知识判断A,B门店次日是否需要增派工作人员.
.表2是B门店某日购买口罩的人数与等待时间的统计表.请你运用所学的统计知识判断A,B门店次日是否需要增派工作人员.
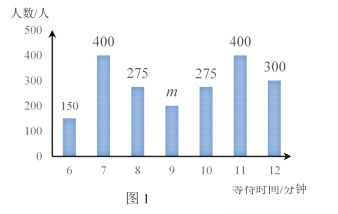
表1
时间段 | 等待9分钟/人 |
14:00~14:30 | 10 |
14:30~15:00 | 20 |
15:00~15:30 | 15 |
15:30~16:00 | 5 |
表2
等待时间 |
|
|
|
|
人数/人 |
|
|
|
|
查看答案和解析>>
科目: 来源: 题型:
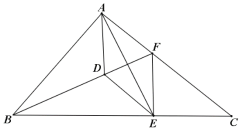
【题目】如图,点E,F分别在△ABC的边BC和AC上,点A,E关于BF对称.点D在BF上,且AD∥EF.
(1)求证:四边形ADEF为菱形;
(2)如果∠ABC=2∠DAE,AD=3,FC=5,求AB.
查看答案和解析>>
科目: 来源: 题型:
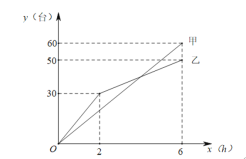
【题目】甲、乙两个电子团队维护一批电脑,维护电脑的台数y(台)与维护需要的工作时间x(h)(0≤x≤6)之间关系如图所示,请依据图象提供的信息解答下列问题:
(1)求乙队维护电脑的台数y(台)关于维护的时间x(h)的关系式;
(2)当x为多少时,甲、乙两队维护的电脑台数一样.
查看答案和解析>>
科目: 来源: 题型:
【题目】我国古代重要建筑的室内上方,通常会在正中部位做出向上凸起的穹窿状装饰,称为藻井.北京故宫博物院内的太和殿上方即有藻井(图1),全称为龙凤角蝉云龙随瓣枋套方八角浑金蟠龙藻井.它展示出精美的装饰空间和造型艺术.从分层构造上来看,太和殿藻井由三层组成:最下层为方井,中层为八角井,上层为圆井.图2是由图1抽象出的平面图形.若最下层方井边长为1,在图2中随机取一点,则此点取自圆内的概率为( )

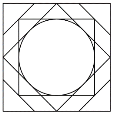
图1 图2
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,以D为顶点的抛物线y=﹣x2+bx+c交x轴于A、B两点,交y轴于点C,直线BC的表达式为y=﹣x+3.
(1)求抛物线的表达式;
(2)在直线BC上有一点P,使PO+PA的值最小,求点P的坐标;
(3)在x轴上是否存在一点Q,使得以A、C、Q为顶点的三角形与△BCD相似?若存在,请求出点Q的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com