
科目: 来源: 题型:
【题目】某校为了解初三300名学生每天做家庭作业的时间情况,从中随机抽取50名学生进行抽样调查,按做作业的时间t(单位:小时),将学生分成四类:A类(![]() ),B类(
),B类(![]() ),C类(
),C类(![]() ),D类(
),D类(![]() ),绘制成尚不完整的条形统计图如图.根据以上信息,解答下列问题:
),绘制成尚不完整的条形统计图如图.根据以上信息,解答下列问题:

(1)补全条形统计图,并估计初三学生做作业时间为D类的学生共有多少人?
(2)抽样调查的A类学生中有3名男生和1名女生,若从中任选2人,求这2人均是男生的概率.
查看答案和解析>>
科目: 来源: 题型:
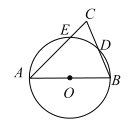
【题目】如图,AB为![]() 的直径,AC,BC分别交
的直径,AC,BC分别交![]() 于点E,D,
于点E,D,![]() ,
,![]() .现给出以下四个结论:①
.现给出以下四个结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正确结论的序号是________.(填写所有正确结论的序号)
.其中正确结论的序号是________.(填写所有正确结论的序号)
查看答案和解析>>
科目: 来源: 题型:
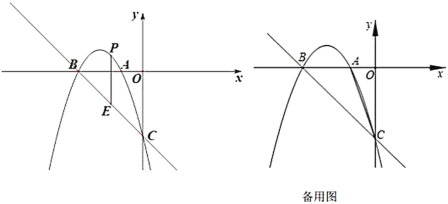
【题目】如图,抛物线![]() 与坐标轴交于点
与坐标轴交于点![]() ,点
,点![]() 和点
和点![]() ,连接
,连接![]() .
.
(1)求抛物线的解析式;
(2)如图,已知点![]() 在线段
在线段![]() 的上方(不包括点
的上方(不包括点![]() 和点
和点![]() ),过
),过![]() 点作
点作![]() 轴的垂线交直线
轴的垂线交直线![]() 于点
于点![]() ,求线段
,求线段![]() 的最大值;
的最大值;
(3)该抛物线上是否存在点![]() ,使得
,使得![]() ?若存在,求点
?若存在,求点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
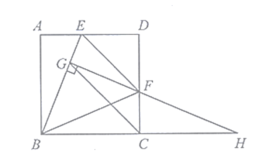
【题目】如图,在正方形![]() 中,
中,![]() 是边
是边![]() 上的动点(与点
上的动点(与点![]() 、
、![]() 不重合),且
不重合),且![]() ,
,![]() 于点
于点![]() ,
,![]() 与
与![]() 的延长线交于点
的延长线交于点![]() ,连接
,连接![]() 、
、![]() .
.
(1)求证:①![]()
![]()
![]() ;②
;②![]() ;
;
(2)若![]() ,在点
,在点![]() 运动过程中,探究:
运动过程中,探究:
①线段![]() 的长度是否改变?若不变,求出这个定值;若改变,请说明理由;
的长度是否改变?若不变,求出这个定值;若改变,请说明理由;
②当![]() 为何值时,
为何值时,![]() 为等腰直角三角形.
为等腰直角三角形.
查看答案和解析>>
科目: 来源: 题型:
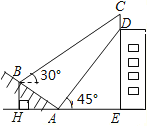
【题目】如图,某大楼的顶部有一块广告牌![]() ,小背在山坡的坡脚
,小背在山坡的坡脚![]() 处测得广告牌底部的仰角为45°,沿坡面
处测得广告牌底部的仰角为45°,沿坡面![]() 向上走到
向上走到![]() 处测得广告牌顶部
处测得广告牌顶部![]() 的仰角为30°.已知山坡
的仰角为30°.已知山坡![]() 的坡度为
的坡度为![]() ,
,![]() 米,
米,![]() 米.
米.
此题考查了折叠的性质、矩形的性质、全等三角形的判定与性质以及勾股定理的应用.熟练掌握折叠的性质是关键.
(1)求点![]() 距地面的高度
距地面的高度![]() ;
;
(2)求广告牌![]() 的高度.(结果保留根号)
的高度.(结果保留根号)
查看答案和解析>>
科目: 来源: 题型:
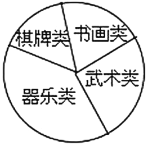
【题目】某校学生会准备调查七年级学生参加“武术类”、“书画类”、“棋牌类”、“器乐类”四类校本课程的人数.
类别 | 频数(人数) | 频率 |
武术类 | 0.20 | |
书画类 | 15 | 0.l5 |
棋牌类 | 25 |
|
器乐类 | ||
合计 |
| 1.00 |
(1)确定调查方式时,甲同学说:“我到七年级(1)班去调查全体同学”;乙同学说:“放学时我到校门口随机调查部分同学”;丙同学说:“我到七年级每个班随机调查一定数量的同学”.请指出哪位同学的调查方式最合理.
(2)他们采用了最为合理的调查方法收集数据,并绘制了如图所示的统计表和扇形统计图.请你根据以上图表提供的信息解答下列问题:
①![]() ____,
____,![]() _____;
_____;
②在扇形统计图中,器乐类所对应扇形的圆心角是_____度;
③若该校七年级有学生460人,请你估计大约有多少学生参加武术类校本课程.
查看答案和解析>>
科目: 来源: 题型:
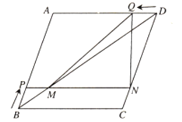
【题目】如图,在菱形ABCD中,AB=5cm,BD=8cm.点P从点B出发,沿BA方向匀速运动,速度为![]() ;同时,点Q从点D出发,沿DA方向匀速运动,速度为1cm/s.过点P作PN∥BC分别交BD,CD于点M,N,连接QM,QN.设运动时间为
;同时,点Q从点D出发,沿DA方向匀速运动,速度为1cm/s.过点P作PN∥BC分别交BD,CD于点M,N,连接QM,QN.设运动时间为![]() .解答下列问题:
.解答下列问题:
(1)当![]() 为何值时,点
为何值时,点![]() 在线段
在线段![]() 的垂直平分线上?
的垂直平分线上?
(2)设![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 的函数关系式;
的函数关系式;
(3)在运动过程中,是否存在某一时刻![]() ,使
,使![]() 的面积为菱形
的面积为菱形![]() 面积的
面积的![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(4)是否存在某一时刻![]() ,使
,使![]() 为等腰三角形?若存在,请直接写出
为等腰三角形?若存在,请直接写出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】(问题提出):有同样大小正方形256个,拼成如图1所示的![]() 的一个大的正方形.请问如果用一条直线穿过这个大正方形的话,最多可以穿过多少个小正方形?
的一个大的正方形.请问如果用一条直线穿过这个大正方形的话,最多可以穿过多少个小正方形?

(问题探究):我们先考虑以下简单的情况:一条直线穿越一个正方形的情况.(如图2)
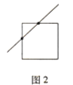
从图中我们可以看出,当一条直线穿过一个小正方形时,这条直线最多与正方形上、下、左、右四条边中的两个边相交,所以当一条直线穿过一个小正方形时,这条直线会与其中某两条边产生两个交点,并且以两个交点为顶点的线段会全部落在小正方形内.
这就启发我们:为了求出直线![]() 最多穿过多少个小正方形,我们可以转而去考虑当直线
最多穿过多少个小正方形,我们可以转而去考虑当直线![]() 穿越由小正方形拼成的大正方形时最多会产生多少个交点.然后由交点数去确定有多少根小线段,进而通过线段的根数确定下正方形的个数.
穿越由小正方形拼成的大正方形时最多会产生多少个交点.然后由交点数去确定有多少根小线段,进而通过线段的根数确定下正方形的个数.
再让我们来考虑![]() 正方形的情况(如图3):
正方形的情况(如图3):
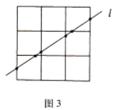
为了让直线穿越更多的小正方形,我们不妨假设直线![]() 右上方至左下方穿过一个
右上方至左下方穿过一个![]() 的正方形,我们从两个方向来分析直线
的正方形,我们从两个方向来分析直线![]() 穿过
穿过![]() 正方形的情况:从上下来看,这条直线由下至上最多可穿过上下平行的两条线段;从左右来看,这条直线最多可穿过左右平行的四条线段;这样直线
正方形的情况:从上下来看,这条直线由下至上最多可穿过上下平行的两条线段;从左右来看,这条直线最多可穿过左右平行的四条线段;这样直线![]() 最多可穿过
最多可穿过![]() 的大正方形中的六条线段,从而直线
的大正方形中的六条线段,从而直线![]() 上会产生6个交点,这6个交点之间的5条线段,每条会落在一个不同的正方形内,因此直线
上会产生6个交点,这6个交点之间的5条线段,每条会落在一个不同的正方形内,因此直线![]() 最多能经过5个小正方形.
最多能经过5个小正方形.
(问题解决):
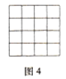
(1)有同样大小的小正方形16个,拼成如图4所示的![]() 的一个大的正方形.如果用一条直线穿过这个大正方形的话,最多可以穿过_________个小正方形.
的一个大的正方形.如果用一条直线穿过这个大正方形的话,最多可以穿过_________个小正方形.
(2)有同样大小的小正方形256个,拼成![]() 的一个大的正方形.如果用一条直线穿过这个大正方形的话,最多可以穿过___________个小正方形.
的一个大的正方形.如果用一条直线穿过这个大正方形的话,最多可以穿过___________个小正方形.
(3)如果用一条直线穿过![]() 的大正方形的话,最多可以穿过___________个小正方形.
的大正方形的话,最多可以穿过___________个小正方形.
(问题拓展):
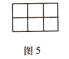
(4)如果用一条直线穿过![]() 的大长方形的话(如图5),最多可以穿过个___________小正方形.
的大长方形的话(如图5),最多可以穿过个___________小正方形.
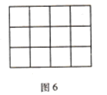
(5)如果用一条直线穿过![]() 的大长方形的话(如图6),最多可以穿过___________个小正方形.
的大长方形的话(如图6),最多可以穿过___________个小正方形.
(6)如果用一条直线穿过![]() 的大长方形的话,最多可以穿过________个小正方形.
的大长方形的话,最多可以穿过________个小正方形.
(类比探究):
由二维的平面我们可以联想到三维的立体空间,平面中的正方形中四条边可联想到正方体中的正方形的六个面,类比上面问题解决的方法解决如下问题:
(7)如图7有同样大小的小正方体8个,拼成如图所示的![]() 的一个大的正方体.如果用一条直线穿过这个大正方体的话,最多可以穿过___________个小正方体.
的一个大的正方体.如果用一条直线穿过这个大正方体的话,最多可以穿过___________个小正方体.
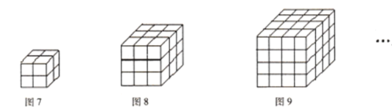
(8)如果用一条直线穿过![]() 的大正方体的话,最多可以穿过_________个小正方体.
的大正方体的话,最多可以穿过_________个小正方体.
查看答案和解析>>
科目: 来源: 题型:
【题目】饮料厂生产某品牌的饮料成本是每瓶5元,每天的生产量不超过9000瓶.根据市场调查,以单价8元批发给经销商,经销商每天愿意经销5000瓶,并且表示单价每降价0.1元,经销商每天愿意多经销500瓶.
(1)求出饮料厂每天的利润![]() (元)与批发单价
(元)与批发单价![]() (元)之间的函数关系式;
(元)之间的函数关系式;
(2)批发单价定为多少元时,饮料厂每天的利润最大,最大利润是多少元;
(3)如果该饮料厂要使每天的利润不低于18750元,且每天的总成本不超过42500元,那么批发单价应控制在什么范围.(每天的总成本![]() 每瓶的成本
每瓶的成本![]() 每天的经销量)
每天的经销量)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com