
科目: 来源: 题型:
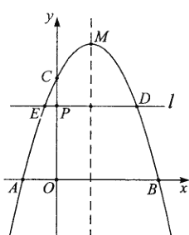
【题目】如图,二次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,
,![]() (点
(点![]() 位于对称轴的左侧),与
位于对称轴的左侧),与![]() 轴交于点
轴交于点![]() .点
.点![]() 为线段
为线段![]() 上一点,过点
上一点,过点![]() 作直线
作直线![]() 轴交图象于点
轴交图象于点![]() ,
,![]() (点
(点![]() 在点
在点![]() 的左侧),且
的左侧),且![]() .
.
(1)求该二次函数的对称轴及![]() 的值.
的值.
(2)将顶点![]() 向右平移
向右平移![]() 个单位至点
个单位至点![]() ,再过点
,再过点![]() 作直线
作直线![]() 的对称点
的对称点![]() ,若点
,若点![]() 在
在![]() 轴上方的图象上一点且到
轴上方的图象上一点且到![]() 轴距离为1,求
轴距离为1,求![]() ,
,![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某学校组织健康知识竞赛,每班参加竞赛的人数相同,成绩为![]() ,
,![]() ,
,![]() ,
,![]() 四个等级,其中相应等级的得分依次记为100分,90分,80分,70分,其中100分和90分为优秀.学校将八年级一班和二班的成绩整理并绘制成如下的统计图与统计表.
四个等级,其中相应等级的得分依次记为100分,90分,80分,70分,其中100分和90分为优秀.学校将八年级一班和二班的成绩整理并绘制成如下的统计图与统计表.
一班竞赛成绩统计图
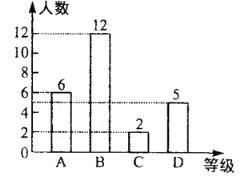
二班竞赛成绩统计图
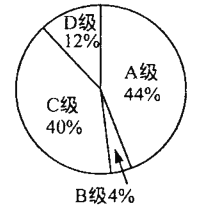
一班和二班竞赛成绩统计表(部分空缺)
成绩 班级 | 众数 | 中位数 | 优秀率 | 平均分 |
一班 | 90 |
|
| 87.6 |
二班 |
| 80 |
|
|
请根据以上图表的信息解答下列问题:
(1)求![]() ,
,![]() ,
,![]() 的值.
的值.
(2)若全校共有750名学生参加竞赛,估计成绩优秀的学生有多少人?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1是一溜娃神器推车,溜娃时该推车底部支架张开后,其框架投影图如图2所示,两支撑轮是分别以点![]() ,
,![]() 为圆心,1.5分米长为半径的圆且与水平地面相切,其支架长
为圆心,1.5分米长为半径的圆且与水平地面相切,其支架长![]() ,竖直支撑柱
,竖直支撑柱![]() 分米,水平座椅
分米,水平座椅![]() 分米,并与靠背
分米,并与靠背![]() 成
成![]() 夹角,推手柄
夹角,推手柄![]() 分米.当张开角
分米.当张开角![]() 时,
时,![]() ,
,![]() ,
,![]() 三点共线,且
三点共线,且![]() ,则
,则![]() 的长度为__________分米;如图3,当张开角
的长度为__________分米;如图3,当张开角![]() 时,折叠支撑柱以上座椅部分绕着点
时,折叠支撑柱以上座椅部分绕着点![]() 逆时针旋转使
逆时针旋转使![]() 点与圆心
点与圆心![]() 重合,此时手柄
重合,此时手柄![]() 绕着点
绕着点![]() 顺时针旋转
顺时针旋转![]() 至
至![]() 处,则
处,则![]() 到地面的距离是____________分米.
到地面的距离是____________分米.
图1 图2
图2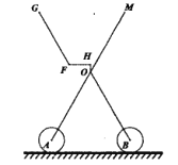 图3
图3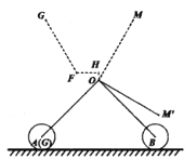
查看答案和解析>>
科目: 来源: 题型:
【题目】已知二次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() (点
(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() ,顶点为
,顶点为![]() .
.
(Ⅰ)当![]() 时,求二次函数的最大值;
时,求二次函数的最大值;
(Ⅱ)当![]() 时,点
时,点![]() 是
是![]() 轴上的点,
轴上的点,![]() ,将点
,将点![]() 绕点
绕点![]() 顺时针旋转90°得到点
顺时针旋转90°得到点![]() ,点
,点![]() 恰好落在该二次函数的图象上,求
恰好落在该二次函数的图象上,求![]() 的值;
的值;
(Ⅲ)![]() 是该二次函数图象上的一点,在(Ⅱ)的条件下,连接
是该二次函数图象上的一点,在(Ⅱ)的条件下,连接![]() ,
,![]() ,使
,使![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,![]() 为原点,点
为原点,点![]() ,点
,点![]() .以
.以![]() 为一边作等边三角形
为一边作等边三角形![]() ,点
,点![]() 在第二象限.
在第二象限.
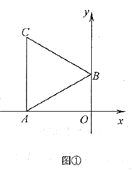
(Ⅰ)如图①,求点![]() 的坐标;
的坐标;
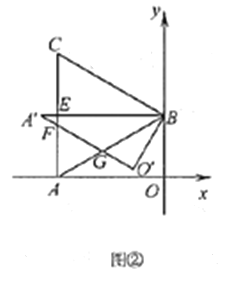
(Ⅱ)将![]() 绕点
绕点![]() 顺时针旋转得
顺时针旋转得![]() ,点
,点![]() 旋转后的对应点为
旋转后的对应点为![]() .
.
①如图②,当旋转角为30°时,![]() 与
与![]() 分别交于点
分别交于点![]() 与
与![]() 交于点
交于点![]() ,求
,求![]() 与
与![]() 公共部分面积
公共部分面积![]() 的值;
的值;
②若![]() 为线段
为线段![]() 的中点,求
的中点,求![]() 长的取值范围(直接写出结果即可).
长的取值范围(直接写出结果即可).
查看答案和解析>>
科目: 来源: 题型:
【题目】某校开展“文明在行动”的志愿者活动,准备购买某一品牌书包送到希望学校.在![]() 商店,无论一次购买多少,价格均为每个50元.在
商店,无论一次购买多少,价格均为每个50元.在![]() 商店,一次购买数量不超过10个时,价格为每个60元;一次购买数量超过10个时,超出10个部分打八折.设一次购买该品牌书包的数量为x个.
商店,一次购买数量不超过10个时,价格为每个60元;一次购买数量超过10个时,超出10个部分打八折.设一次购买该品牌书包的数量为x个.
(Ⅰ)根据题意填表:
一次购买数量/个 | 5 | 10 | 15 | … |
| 500 | … | ||
| 600 | … |
(Ⅱ)设在![]() 商店花费
商店花费![]() 元,在
元,在![]() 商店花费
商店花费![]() 元,分别求出
元,分别求出![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(Ⅲ)根据题意填空;
①若小丽在![]() 商店和在
商店和在![]() 商店一次购买书包的数量相同,且花费相同,则她在同一商店一次购买书包的数量为______个.
商店一次购买书包的数量相同,且花费相同,则她在同一商店一次购买书包的数量为______个.
②若小丽在同一商店一次购买书包的数量为50个,则她在![]() 两个商店中的______商店购买花费少;
两个商店中的______商店购买花费少;
③若小丽在同一商店一次购买书包花费了1800元,则她在![]() 两个商店中_______商店购买数量多.
两个商店中_______商店购买数量多.
查看答案和解析>>
科目: 来源: 题型:
【题目】我校八年级有800名学生,在体育中考前进行一次排球模拟测试,从中随机抽取部分学生,根据其测试成绩制作了下面两个统计图,请根据相关信息,解答下列问题:

(1)本次抽取到的学生人数为________,图2中![]() 的值为_________.
的值为_________.
(2)本次调查获取的样本数据的平均数是__________,众数是________,中位数是_________.
(3)根据样本数据,估计我校八年级模拟体测中得12分的学生约有多少人?
查看答案和解析>>
科目: 来源: 题型:
【题目】解不等式组
请结合题意填空,完成本题的解答.
(Ⅰ)解不等式①,得_______________;
(Ⅱ)解不等式②,得_______________;
(Ⅲ)把不等式①和②的解集在数轴上表示出来;
![]()
(Ⅳ)原不等式组的解集为________________.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在每个小正方形边长为1的网格中,点![]() 均在格点上,
均在格点上,![]() 交于点
交于点![]() .
.
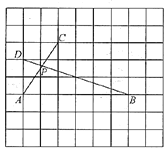
(Ⅰ)![]() 的值为_____________;
的值为_____________;
(Ⅱ)若点![]() 在线段
在线段![]() 上,当
上,当![]() 取得最小值时,请在如图所示的网格中用无刻度的直尺,画出点
取得最小值时,请在如图所示的网格中用无刻度的直尺,画出点![]() ,并简要说明点
,并简要说明点![]() 的位置是如何找到的(不要求证明)_____________.
的位置是如何找到的(不要求证明)_____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com