
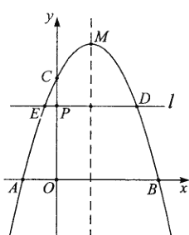
【题目】如图,二次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,
,![]() (点
(点![]() 位于对称轴的左侧),与
位于对称轴的左侧),与![]() 轴交于点
轴交于点![]() .点
.点![]() 为线段
为线段![]() 上一点,过点
上一点,过点![]() 作直线
作直线![]() 轴交图象于点
轴交图象于点![]() ,
,![]() (点
(点![]() 在点
在点![]() 的左侧),且
的左侧),且![]() .
.
(1)求该二次函数的对称轴及![]() 的值.
的值.
(2)将顶点![]() 向右平移
向右平移![]() 个单位至点
个单位至点![]() ,再过点
,再过点![]() 作直线
作直线![]() 的对称点
的对称点![]() ,若点
,若点![]() 在
在![]() 轴上方的图象上一点且到
轴上方的图象上一点且到![]() 轴距离为1,求
轴距离为1,求![]() ,
,![]() 的值.
的值.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】随着生活节奏的加快以及智能手机的普及,外卖点餐逐渐成为越来越多用户的餐饮消费习惯.由此催生了一批外卖点餐平台,已知某外卖平台的送餐费用与送餐距离有关(该平台只给5千米范围内配送),为调査送餐员的送餐收入,现从该平台随机抽取80名点外卖的用户进行统计,按送餐距离分类统计结果如下表:
送餐距离x(千米) | 0 | 1 | 2 | 3 | 4 |
数量 | 12 | 20 | 24 | 16 | 8 |
(1)从这80名点外卖的用户中任取一名用户,该用户的送餐距离不超过3千米的概率为 ;
(2)以这80名用户送餐距离为样本,同一组数据取该小组数据的中间值(例如第二小组(1<x ≤2)的中间值是1.5),试估计利用该平台点外卖用户的平均送餐距离;
(3)若该外卖平台给送餐员的送餐费用与送餐距离有关,不超过2千米时,每份3元;超过2千米但不超4千米时,每份5元;超过4千米时,每份9元. 以给这80名用户所需送餐费用的平均数为依据,若送餐员一天的目标收入不低于150元,试估计一天至少要送多少份外卖?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,∠BAC的平分线交BC于点D,E为AB上的一点,DE=DC,以D为圆心,DB长为半径作⊙D,AB=5,EB=3.
(1)求证:AC是⊙D的切线;
(2)求线段AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现
如图![]() , 在
, 在![]() 和
和![]() 中,
中,![]() ,
,![]() ,
,![]() , 连接
, 连接![]() ,
,![]() 交于点
交于点![]() .填空:①
.填空:①![]() 的值为 :②
的值为 :②![]() 的度数为
的度数为
(2)类比探究
如图![]() , 在
, 在![]() 和
和![]() 中,
中,![]() ,
,![]() , 连接
, 连接![]() 交
交![]() 的延长线于点
的延长线于点![]() .请求出
.请求出![]() 能的值及
能的值及![]() 的度数, 并说明理由;
的度数, 并说明理由;
(3)拓展延伸
在![]() 的条件下, 将
的条件下, 将![]() 绕点
绕点![]() 在平面内旋转,
在平面内旋转,![]() 所在直线交于点
所在直线交于点![]() , 若
, 若![]() ,
,![]() ,请直接写出当点
,请直接写出当点![]() 与点
与点![]() 重合时
重合时![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展“文明在行动”的志愿者活动,准备购买某一品牌书包送到希望学校.在![]() 商店,无论一次购买多少,价格均为每个50元.在
商店,无论一次购买多少,价格均为每个50元.在![]() 商店,一次购买数量不超过10个时,价格为每个60元;一次购买数量超过10个时,超出10个部分打八折.设一次购买该品牌书包的数量为x个.
商店,一次购买数量不超过10个时,价格为每个60元;一次购买数量超过10个时,超出10个部分打八折.设一次购买该品牌书包的数量为x个.
(Ⅰ)根据题意填表:
一次购买数量/个 | 5 | 10 | 15 | … |
| 500 | … | ||
| 600 | … |
(Ⅱ)设在![]() 商店花费
商店花费![]() 元,在
元,在![]() 商店花费
商店花费![]() 元,分别求出
元,分别求出![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(Ⅲ)根据题意填空;
①若小丽在![]() 商店和在
商店和在![]() 商店一次购买书包的数量相同,且花费相同,则她在同一商店一次购买书包的数量为______个.
商店一次购买书包的数量相同,且花费相同,则她在同一商店一次购买书包的数量为______个.
②若小丽在同一商店一次购买书包的数量为50个,则她在![]() 两个商店中的______商店购买花费少;
两个商店中的______商店购买花费少;
③若小丽在同一商店一次购买书包花费了1800元,则她在![]() 两个商店中_______商店购买数量多.
两个商店中_______商店购买数量多.
查看答案和解析>>
科目:初中数学 来源: 题型:
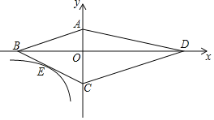
【题目】如图,四边形ABCD的顶点都在坐标轴上,若AB∥CD,![]() AOB与
AOB与![]() COD面积分别为8和18,若双曲线y=
COD面积分别为8和18,若双曲线y=![]() 恰好经过BC的中点E,则k的值为_____.
恰好经过BC的中点E,则k的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实行垃圾分类和垃圾资源化利用,关系广大人民群众生活环境,关系节约使用资源,也是社会文明水平的一个重要体现.某环保公司研发了甲、乙两种智能设备,可利用最新技术将干垃圾进行分选破碎制成固化成型燃料棒,干垃圾由此变身新型清洁燃料.某垃圾处理厂从环保公司购入以上两种智能设备若干,已知购买甲型智能设备花费![]() 万元,购买乙型智能设备花费
万元,购买乙型智能设备花费![]() 万元,购买的两种设备数量相同,且两种智能设备的单价和为
万元,购买的两种设备数量相同,且两种智能设备的单价和为![]() 万元.
万元.
![]() 求甲、乙两种智能设备单价;
求甲、乙两种智能设备单价;
![]() 垃圾处理厂利用智能设备生产燃料棒,并将产品出售.已知燃料棒的成本由人力成本和物资成本两部分组成,其中物资成本占总成本的
垃圾处理厂利用智能设备生产燃料棒,并将产品出售.已知燃料棒的成本由人力成本和物资成本两部分组成,其中物资成本占总成本的![]() ,且生产每吨燃料棒所需人力成本比物资成本的倍
,且生产每吨燃料棒所需人力成本比物资成本的倍![]() 还多
还多![]() 元.调查发现,若燃料棒售价为每吨
元.调查发现,若燃料棒售价为每吨![]() 元,平均每天可售出
元,平均每天可售出![]() 吨,而当销售价每降低
吨,而当销售价每降低![]() 元,平均每天可多售出
元,平均每天可多售出![]() 吨.垃圾处理厂想使这种燃料棒的销售利润平均每天达到
吨.垃圾处理厂想使这种燃料棒的销售利润平均每天达到![]() 元,且保证售价在每吨
元,且保证售价在每吨![]() 元基础上降价幅度不超过
元基础上降价幅度不超过![]() ,求每吨燃料棒售价应为多少元?
,求每吨燃料棒售价应为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是等边三角形ABC内一点,且PA=3,PB=4, PC=5,若将△APB绕着点B逆时针旋转后得到△CQB,则∠APB的度数______.

查看答案和解析>>
科目:初中数学 来源: 题型:
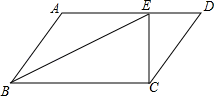
【题目】如图,在平行四边形ABCD中,E为AD边上一点,BE平分∠ABC,连接CE,已知DE=6,CE=8,AE=10.
(1)求AB的长;
(2)求平行四边形ABCD的面积;
(3)求cos∠AEB.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com