
【题目】(1)问题发现
如图![]() , 在
, 在![]() 和
和![]() 中,
中,![]() ,
,![]() ,
,![]() , 连接
, 连接![]() ,
,![]() 交于点
交于点![]() .填空:①
.填空:①![]() 的值为 :②
的值为 :②![]() 的度数为
的度数为
(2)类比探究
如图![]() , 在
, 在![]() 和
和![]() 中,
中,![]() ,
,![]() , 连接
, 连接![]() 交
交![]() 的延长线于点
的延长线于点![]() .请求出
.请求出![]() 能的值及
能的值及![]() 的度数, 并说明理由;
的度数, 并说明理由;
(3)拓展延伸
在![]() 的条件下, 将
的条件下, 将![]() 绕点
绕点![]() 在平面内旋转,
在平面内旋转,![]() 所在直线交于点
所在直线交于点![]() , 若
, 若![]() ,
,![]() ,请直接写出当点
,请直接写出当点![]() 与点
与点![]() 重合时
重合时![]() 的长.
的长.

【答案】(1)![]() ;
;![]() (2)
(2)![]() .理由见解析(3)
.理由见解析(3)![]() 的长为
的长为![]() 或
或![]() .
.
【解析】
(1)①证明![]() ,得到AC=BD,比值为1;②由
,得到AC=BD,比值为1;②由![]() 得
得![]() ,根据三角形内角和定理得,
,根据三角形内角和定理得,![]() =
=![]() .
.
(2)根据两边的比相等且夹角相等可得![]() ∽
∽![]() ,则
,则![]() ,由全等三角形的性质得
,由全等三角形的性质得![]() 的度数.
的度数.
(3)正确画出图形,当点C与点M重合时,有两种情况:如图3和如图4,同理可得![]() ,则
,则![]() ,
,![]() ,可得AC的长.
,可得AC的长.
(1)![]() ;
;![]()
①如图1.
∵![]() ,
,
∴![]() ,
,
∵OC=OD,OA=OB,
∴![]() ,
,
∴AC=BD,
∴![]() .
.
②∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
在![]() ,
,
![]() ,
,
=![]() ,
,
=![]() ,
,
故答案为:1,![]() .
.
(2)![]() .理由如下:
.理由如下:
在![]() ,中
,中![]()
∴![]() ,同理可得
,同理可得![]()
∴![]()
∵![]()
∴![]()
∴![]() ∽
∽![]()
∴![]()
![]()
∴![]()
(3)拓展延伸
①点C与点M重合时,如图3,同理得:![]() ,
,
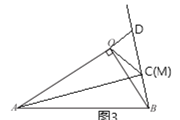
∴![]() ,
,![]() ,
,
设![]() ,则
,则![]() ,
,
Rt△COD中,![]() ,OD=1,
,OD=1,
∴![]() ,
,![]() ,
,
Rt△AOB中,![]() ,
,![]() ,
,
∴![]() ,
,
在RtAMB中,由勾股定理得:
![]() ,
,
![]() ,
,
![]() ,
,
解得:![]() ,
,![]() ,
,
∴![]() ;
;
②点C与点M重合时,如图4,
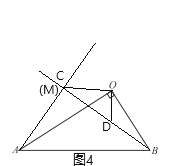
同理得:![]() ,
,![]() ,
,
设![]() ,则
,则![]() ,
,
在RtAMB中,由勾股定理得:
![]() ,
,
![]() ,
,
![]() ,
,
解得:![]() ,
,![]() ,
,
∴![]()
综上所述:![]() 的长为
的长为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】某公司生产的一种产品按照质量由高到低分为A,B,C,D四级,为了增加产量、提高质量,该公司改进了一次生产工艺,使得生产总量增加了一倍.为了解新生产工艺的效果,对改进生产工艺前、后的四级产品的占比情况进行了统计,绘制了如下扇形图:
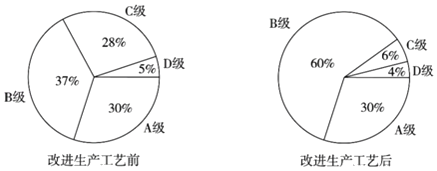
根据以上信息,下列推断合理的是( )
A.改进生产工艺后,A级产品的数量没有变化
B.改进生产工艺后,B级产品的数量增加了不到一倍
C.改进生产工艺后,C级产品的数量减少
D.改进生产工艺后,D级产品的数量减少
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形![]() 中,
中,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 边上的点,
边上的点,![]() 与
与![]() 交于点
交于点![]() .
.
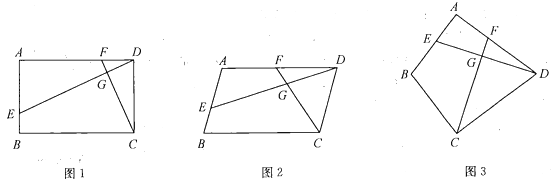
(1)如图1,若四边形![]() 是矩形,且
是矩形,且![]() ,求证:
,求证:![]() ;
;
(2)如图2,若四边形![]() 是平行四边形,试探究:当
是平行四边形,试探究:当![]() 与
与![]() 满足什么关系时,使得
满足什么关系时,使得![]() 成立?并证明你的结论;
成立?并证明你的结论;
(3)如图3,若![]() ,
,![]() ,
,![]() ,
,![]() ,请直接写出
,请直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小丽早晨6:00从家里出发,骑车去菜场买菜,然后从菜场返回家中.小丽离家的路程![]() (米)和所经过的时间
(米)和所经过的时间![]() (分)之间的函数图象如图所示,请根据图象回答下列问题:
(分)之间的函数图象如图所示,请根据图象回答下列问题:

(1)小丽去菜场途中的速度是多少?在菜场逗留了多长时间?
(2)小丽几点几分返回到家?
查看答案和解析>>
科目:初中数学 来源: 题型:
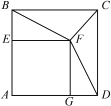
【题目】如图,正方形AEFG的顶点E、G在正方形ABCD的边AB、AD上,连接BF、DF.
![]() (1)求证:BF=DF;
(1)求证:BF=DF;
(2)连接CF,请直接写出![]() 的值为__________(不必写出计算过程).
的值为__________(不必写出计算过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我校八年级有800名学生,在体育中考前进行一次排球模拟测试,从中随机抽取部分学生,根据其测试成绩制作了下面两个统计图,请根据相关信息,解答下列问题:

(1)本次抽取到的学生人数为________,图2中![]() 的值为_________.
的值为_________.
(2)本次调查获取的样本数据的平均数是__________,众数是________,中位数是_________.
(3)根据样本数据,估计我校八年级模拟体测中得12分的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
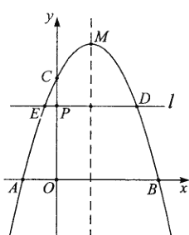
【题目】如图,二次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,
,![]() (点
(点![]() 位于对称轴的左侧),与
位于对称轴的左侧),与![]() 轴交于点
轴交于点![]() .点
.点![]() 为线段
为线段![]() 上一点,过点
上一点,过点![]() 作直线
作直线![]() 轴交图象于点
轴交图象于点![]() ,
,![]() (点
(点![]() 在点
在点![]() 的左侧),且
的左侧),且![]() .
.
(1)求该二次函数的对称轴及![]() 的值.
的值.
(2)将顶点![]() 向右平移
向右平移![]() 个单位至点
个单位至点![]() ,再过点
,再过点![]() 作直线
作直线![]() 的对称点
的对称点![]() ,若点
,若点![]() 在
在![]() 轴上方的图象上一点且到
轴上方的图象上一点且到![]() 轴距离为1,求
轴距离为1,求![]() ,
,![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
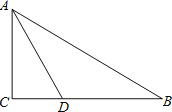
【题目】已知:如图,在![]() 中,
中,![]() 的角平分线
的角平分线![]() 交
交![]() 边于
边于![]() .
.
(1)以![]() 边上一点
边上一点![]() 为圆心,过
为圆心,过![]() 两点作
两点作![]() (不写作法,保留作图痕迹),再判断直线
(不写作法,保留作图痕迹),再判断直线![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)若(1)中的![]() 与
与![]() 边的另一个交点为
边的另一个交点为![]() ,
,![]() ,求线段
,求线段![]() 与劣弧
与劣弧![]() 所围成的图形面积.(结果保留根号和
所围成的图形面积.(结果保留根号和![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com