
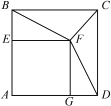
【题目】如图,正方形AEFG的顶点E、G在正方形ABCD的边AB、AD上,连接BF、DF.
![]() (1)求证:BF=DF;
(1)求证:BF=DF;
(2)连接CF,请直接写出![]() 的值为__________(不必写出计算过程).
的值为__________(不必写出计算过程).
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:
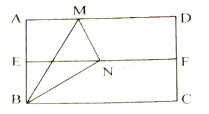
【题目】如图,在矩形纸片![]() 中,
中,![]() ,对折矩形纸片
,对折矩形纸片![]() ,使
,使![]() 与
与![]() 重合,折痕为
重合,折痕为![]() ,展平后再过点
,展平后再过点![]() 折叠,使点
折叠,使点![]() 落在
落在![]() 上的点
上的点![]() ,折痕为
,折痕为![]() .再次展平,连接
.再次展平,连接![]() ,
,![]() ,有下列结论:①
,有下列结论:①![]() ;②
;②![]() 与
与![]() 相似;③
相似;③![]() 的长为
的长为![]() :④若
:④若![]() 分别为线段
分别为线段![]() 上的动点(不包含端点),则
上的动点(不包含端点),则![]() 的最小值是
的最小值是![]() .其中正确结论的序号是__________.
.其中正确结论的序号是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请认真阅读下面的数学探究,并完成所提出的问题.
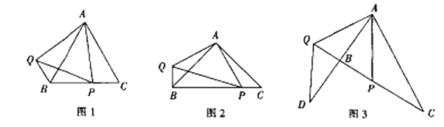
(1)探究1:如图1,在边长为![]() 的等边三角形
的等边三角形![]() 中,
中,![]() 是
是![]() 边上任意一点,连接
边上任意一点,连接![]() ,将
,将![]() 绕点
绕点![]() 按顺时针方向旋转至
按顺时针方向旋转至![]() 处,连接
处,连接![]() ,求
,求![]() 面积的最小值.
面积的最小值.
(2)探究2:如图2,若![]() 是腰长为
是腰长为![]() 的等腰直角三角形,
的等腰直角三角形,![]() ,(1)中的其他条件不变,请求出此时
,(1)中的其他条件不变,请求出此时![]() 面积的最小值.
面积的最小值.
(3)探究3:如图3,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 边上任意一点,连接
边上任意一点,连接![]() ,将
,将![]() 绕点
绕点![]() 按顺时针方向旋转至
按顺时针方向旋转至![]() 处,
处,![]() 、
、![]() 、
、![]() 三点共线,连接
三点共线,连接![]() ,求
,求![]() 的面积的最小值.
的面积的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,∠BAC的平分线交BC于点D,E为AB上的一点,DE=DC,以D为圆心,DB长为半径作⊙D,AB=5,EB=3.
(1)求证:AC是⊙D的切线;
(2)求线段AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,![]() ,
,![]() ,
,![]() 轴,如图1,
轴,如图1,![]() ,且
,且![]()
![]() .
.
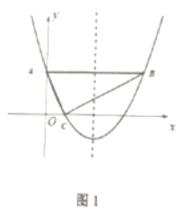
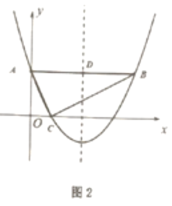
(1)![]() 点坐标为__________,
点坐标为__________,![]() 点坐标为__________;
点坐标为__________;
(2)求过![]() 、
、![]() 、
、![]() 三点的抛物线表达式;
三点的抛物线表达式;
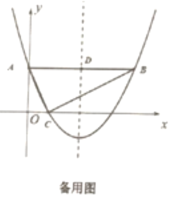
(3)如图2,抛物线对称轴与![]() 交于点
交于点![]() ,现有一点
,现有一点![]() 从点
从点![]() 出发,以每秒1个单位的速度在
出发,以每秒1个单位的速度在![]() 上向点
上向点![]() 运动,另一点
运动,另一点![]() 从点
从点![]() 与点
与点![]() 同时出发,以每秒5个单位在抛物线对称轴上运动.当点
同时出发,以每秒5个单位在抛物线对称轴上运动.当点![]() 到达
到达![]() 点时,点
点时,点![]() 、
、![]() 同时停止运动,问点
同时停止运动,问点![]() 、
、![]() 运动到何处时,
运动到何处时,![]() 面积最大,试求出最大面积.
面积最大,试求出最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现
如图![]() , 在
, 在![]() 和
和![]() 中,
中,![]() ,
,![]() ,
,![]() , 连接
, 连接![]() ,
,![]() 交于点
交于点![]() .填空:①
.填空:①![]() 的值为 :②
的值为 :②![]() 的度数为
的度数为
(2)类比探究
如图![]() , 在
, 在![]() 和
和![]() 中,
中,![]() ,
,![]() , 连接
, 连接![]() 交
交![]() 的延长线于点
的延长线于点![]() .请求出
.请求出![]() 能的值及
能的值及![]() 的度数, 并说明理由;
的度数, 并说明理由;
(3)拓展延伸
在![]() 的条件下, 将
的条件下, 将![]() 绕点
绕点![]() 在平面内旋转,
在平面内旋转,![]() 所在直线交于点
所在直线交于点![]() , 若
, 若![]() ,
,![]() ,请直接写出当点
,请直接写出当点![]() 与点
与点![]() 重合时
重合时![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展“文明在行动”的志愿者活动,准备购买某一品牌书包送到希望学校.在![]() 商店,无论一次购买多少,价格均为每个50元.在
商店,无论一次购买多少,价格均为每个50元.在![]() 商店,一次购买数量不超过10个时,价格为每个60元;一次购买数量超过10个时,超出10个部分打八折.设一次购买该品牌书包的数量为x个.
商店,一次购买数量不超过10个时,价格为每个60元;一次购买数量超过10个时,超出10个部分打八折.设一次购买该品牌书包的数量为x个.
(Ⅰ)根据题意填表:
一次购买数量/个 | 5 | 10 | 15 | … |
| 500 | … | ||
| 600 | … |
(Ⅱ)设在![]() 商店花费
商店花费![]() 元,在
元,在![]() 商店花费
商店花费![]() 元,分别求出
元,分别求出![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(Ⅲ)根据题意填空;
①若小丽在![]() 商店和在
商店和在![]() 商店一次购买书包的数量相同,且花费相同,则她在同一商店一次购买书包的数量为______个.
商店一次购买书包的数量相同,且花费相同,则她在同一商店一次购买书包的数量为______个.
②若小丽在同一商店一次购买书包的数量为50个,则她在![]() 两个商店中的______商店购买花费少;
两个商店中的______商店购买花费少;
③若小丽在同一商店一次购买书包花费了1800元,则她在![]() 两个商店中_______商店购买数量多.
两个商店中_______商店购买数量多.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实行垃圾分类和垃圾资源化利用,关系广大人民群众生活环境,关系节约使用资源,也是社会文明水平的一个重要体现.某环保公司研发了甲、乙两种智能设备,可利用最新技术将干垃圾进行分选破碎制成固化成型燃料棒,干垃圾由此变身新型清洁燃料.某垃圾处理厂从环保公司购入以上两种智能设备若干,已知购买甲型智能设备花费![]() 万元,购买乙型智能设备花费
万元,购买乙型智能设备花费![]() 万元,购买的两种设备数量相同,且两种智能设备的单价和为
万元,购买的两种设备数量相同,且两种智能设备的单价和为![]() 万元.
万元.
![]() 求甲、乙两种智能设备单价;
求甲、乙两种智能设备单价;
![]() 垃圾处理厂利用智能设备生产燃料棒,并将产品出售.已知燃料棒的成本由人力成本和物资成本两部分组成,其中物资成本占总成本的
垃圾处理厂利用智能设备生产燃料棒,并将产品出售.已知燃料棒的成本由人力成本和物资成本两部分组成,其中物资成本占总成本的![]() ,且生产每吨燃料棒所需人力成本比物资成本的倍
,且生产每吨燃料棒所需人力成本比物资成本的倍![]() 还多
还多![]() 元.调查发现,若燃料棒售价为每吨
元.调查发现,若燃料棒售价为每吨![]() 元,平均每天可售出
元,平均每天可售出![]() 吨,而当销售价每降低
吨,而当销售价每降低![]() 元,平均每天可多售出
元,平均每天可多售出![]() 吨.垃圾处理厂想使这种燃料棒的销售利润平均每天达到
吨.垃圾处理厂想使这种燃料棒的销售利润平均每天达到![]() 元,且保证售价在每吨
元,且保证售价在每吨![]() 元基础上降价幅度不超过
元基础上降价幅度不超过![]() ,求每吨燃料棒售价应为多少元?
,求每吨燃料棒售价应为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2022年在北京将举办第24届冬季奥运会,很多学校都开展了冰雪项目学习.如图,滑雪轨道由AB、BC两部分组成,AB、BC的长度都为200米,一位同学乘滑雪板沿此轨道由A点滑到了C点,若AB与水平面的夹角α为20°,BC与水平面的夹角β为45°,则他下降的高度为___________米(精确到1米,![]() ,sin20o=0.3420,tan20o=0.3640,cos20o=0.9400).
,sin20o=0.3420,tan20o=0.3640,cos20o=0.9400).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com