
【题目】在平面直角坐标系中,![]() ,
,![]() ,
,![]() 轴,如图1,
轴,如图1,![]() ,且
,且![]()
![]() .
.
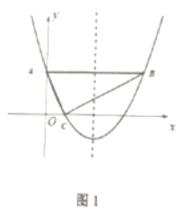
(1)![]() 点坐标为__________,
点坐标为__________,![]() 点坐标为__________;
点坐标为__________;
(2)求过![]() 、
、![]() 、
、![]() 三点的抛物线表达式;
三点的抛物线表达式;
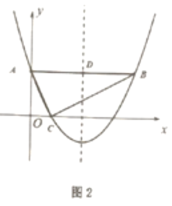
(3)如图2,抛物线对称轴与![]() 交于点
交于点![]() ,现有一点
,现有一点![]() 从点
从点![]() 出发,以每秒1个单位的速度在
出发,以每秒1个单位的速度在![]() 上向点
上向点![]() 运动,另一点
运动,另一点![]() 从点
从点![]() 与点
与点![]() 同时出发,以每秒5个单位在抛物线对称轴上运动.当点
同时出发,以每秒5个单位在抛物线对称轴上运动.当点![]() 到达
到达![]() 点时,点
点时,点![]() 、
、![]() 同时停止运动,问点
同时停止运动,问点![]() 、
、![]() 运动到何处时,
运动到何处时,![]() 面积最大,试求出最大面积.
面积最大,试求出最大面积.
【答案】(1)![]() ;(2)
;(2) ![]() (3) 当点
(3) 当点![]() 坐标为
坐标为![]() 点
点![]() 坐标为
坐标为![]() 或
或![]() 时,
时,![]() 面积最大,最大面积为
面积最大,最大面积为![]()
【解析】
(1)由C(1,0)得OC=1,由![]() 1:2得OA=2,即A(0,2),由勾股定理求出AC的长,过点B 作BE⊥x轴,证明△ACO∽△CBE,可得BE,CE的长,从而可得结论;
1:2得OA=2,即A(0,2),由勾股定理求出AC的长,过点B 作BE⊥x轴,证明△ACO∽△CBE,可得BE,CE的长,从而可得结论;
(2)设抛物线表达式为y=ax2+bx+c,把A、B、C三点坐标代入,求解方程组得到a、b、c的值即可;
(3)根据题意求出BP=5-t,DQ=5t,结合三角形面积公式可得到![]() ,求出其最大值时即可得出P、Q坐标.
,求出其最大值时即可得出P、Q坐标.
(1)∵C(1,0),
∴OC=1,
∵![]() 1:2.
1:2.
∴OA=2,
∴A(0,2),
∴AC=![]() ,
,
∵![]() ,
,
∴BC=2![]() ,
,
过点B 作BE⊥x轴,垂足为点E,如图,

∵∠ACB=90°,
∴∠ACO+∠BCE=90°,
∵∠OAC+∠ACO=90°,
∴∠OAC=∠BCE,
又∠AOC=∠BEC=90°,
∴△ACO∽△CBE,
∴![]() ,
,
∴CE=4,BE=2,
∴OE=OC+CE=5,
∴B(5,0),
故答案为:![]() ,
,![]() ;
;
(2)设过![]() 、
、![]() 、
、![]() 三点的抛物线表达式为y=ax2+bx+c,
三点的抛物线表达式为y=ax2+bx+c,
把A(0,2)、B(5,2)、C(1,0)三点坐标代入,得:
 ,
,
解得, ,
,
所以,过![]() 、
、![]() 、
、![]() 三点的抛物线表达式为:
三点的抛物线表达式为:![]() ;
;
(3)解:在Rt△ABC中,BC=2![]() ,AC=
,AC=![]() ,∠ACB=90°,
,∠ACB=90°,
所以,AB=![]() ,
,
设运动![]() 秒时,
秒时,![]() 面积最大,且
面积最大,且![]() ,
,
则![]() ,
,![]() ,
,
![]() ,
,
![]() 当
当 时,
时,
面积最大值![]() ,
,
![]() 此时点
此时点![]() 坐标为
坐标为![]() ,
,
![]() 当点
当点![]() 向上运动时,
向上运动时,![]() 点坐标为
点坐标为![]()
当点![]() 向下运动时,
向下运动时,![]() 点坐标为
点坐标为![]()
![]() 综上所述,当点
综上所述,当点![]() 坐标为
坐标为![]() ,点
,点![]() 坐标为
坐标为![]() 或
或![]() 时,
时,![]() 面积最大,最大面积为
面积最大,最大面积为![]() .
.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
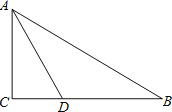
【题目】已知:如图,在![]() 中,
中,![]() 的角平分线
的角平分线![]() 交
交![]() 边于
边于![]() .
.
(1)以![]() 边上一点
边上一点![]() 为圆心,过
为圆心,过![]() 两点作
两点作![]() (不写作法,保留作图痕迹),再判断直线
(不写作法,保留作图痕迹),再判断直线![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)若(1)中的![]() 与
与![]() 边的另一个交点为
边的另一个交点为![]() ,
,![]() ,求线段
,求线段![]() 与劣弧
与劣弧![]() 所围成的图形面积.(结果保留根号和
所围成的图形面积.(结果保留根号和![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
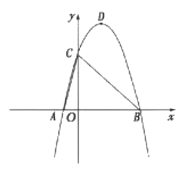
【题目】如图,在平面直角坐标系中,抛物线![]() 经过A(-1,0)B(4,0),C(0,4)三点.
经过A(-1,0)B(4,0),C(0,4)三点.
(1)求抛物线的解析式及顶点D的坐标;
(2)将(1)中的抛物线向下平移![]() 个长度单位,再向左平移h(h>0)个长度单位,得到新抛物线.若新抛物线的顶点
个长度单位,再向左平移h(h>0)个长度单位,得到新抛物线.若新抛物线的顶点![]() 在△ABC内,求h的取值范围;
在△ABC内,求h的取值范围;
(3)点P为线段BC上的一动点(点P不与点B,C重合),过点P作x轴的垂线交(1)中的抛物线于点Q,当△PQC与△ABC相似时,求△PQC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某药店购进一批消毒液,计划每瓶标价100元,由于疫情得到有效控制,药店决定对这批消毒液全部降价销售,设每次降价的百分率相同,经过连续两次降价后,每瓶售价为81元.
(1)求每次降价的百分率.
(2)若按标价出售,每瓶能盈利100%,问第一次降价后销售消毒液100瓶,第二次降价后至少需要销售多少瓶,总利润才能超过5000元?
查看答案和解析>>
科目:初中数学 来源: 题型:
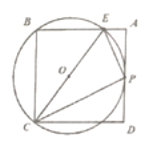
【题目】如图,已知在正方形![]() 中,
中,![]() ,
,![]() 是线段
是线段![]() 上的一动点,连接
上的一动点,连接![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() .以
.以![]() 为直径作
为直径作![]() ,当点
,当点![]() 从点
从点![]() 移动到点
移动到点![]() 时,对应点
时,对应点![]() 也随之运动,则点
也随之运动,则点![]() 运动的路程长度为____________.
运动的路程长度为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
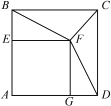
【题目】如图,正方形AEFG的顶点E、G在正方形ABCD的边AB、AD上,连接BF、DF.
![]() (1)求证:BF=DF;
(1)求证:BF=DF;
(2)连接CF,请直接写出![]() 的值为__________(不必写出计算过程).
的值为__________(不必写出计算过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 及一次函数
及一次函数![]() ,将该二次函数在
,将该二次函数在![]() 轴上方的图象沿
轴上方的图象沿![]() 轴翻折到
轴翻折到![]() 轴下方,图象的其余部分不变,得到一个新函数的图象(如图所示),当直线
轴下方,图象的其余部分不变,得到一个新函数的图象(如图所示),当直线![]() 与新函数图象有4个交点时,
与新函数图象有4个交点时,![]() 的取值范围是( )
的取值范围是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
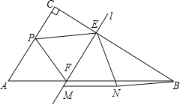
【题目】如图,Rt![]() ABC中,∠C=90°,AC=10,BC=16.动点P以每秒3个单位的速度从点A开始向点C移动,直线l从与AC重合的位置开始,以相同的速度沿CB方向平行移动,且分别与CB,AB边交于E,F两点,点P与直线l同时出发,设运动的时间为t秒,当点P移动到与点C重合时,点P和直线l同时停止运动.在移动过程中,将
ABC中,∠C=90°,AC=10,BC=16.动点P以每秒3个单位的速度从点A开始向点C移动,直线l从与AC重合的位置开始,以相同的速度沿CB方向平行移动,且分别与CB,AB边交于E,F两点,点P与直线l同时出发,设运动的时间为t秒,当点P移动到与点C重合时,点P和直线l同时停止运动.在移动过程中,将![]() PEF绕点E逆时针旋转,使得点P的对应点M落在直线l上,点F的对应点记为点N,连接BN,当BN∥PE时,t的值为_____.
PEF绕点E逆时针旋转,使得点P的对应点M落在直线l上,点F的对应点记为点N,连接BN,当BN∥PE时,t的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
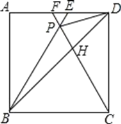
【题目】如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连结BD、DP,BD与CF相交于点H,给出下列结论:①![]() ;②△DFP△BPH;③
;②△DFP△BPH;③![]() ; ④
; ④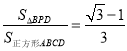 .其中正确的是______.(写出所有正确结论的序号).
.其中正确的是______.(写出所有正确结论的序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com