
【题目】如图,在矩形纸片![]() 中,
中,![]() ,对折矩形纸片
,对折矩形纸片![]() ,使
,使![]() 与
与![]() 重合,折痕为
重合,折痕为![]() ,展平后再过点
,展平后再过点![]() 折叠,使点
折叠,使点![]() 落在
落在![]() 上的点
上的点![]() ,折痕为
,折痕为![]() .再次展平,连接
.再次展平,连接![]() ,
,![]() ,有下列结论:①
,有下列结论:①![]() ;②
;②![]() 与
与![]() 相似;③
相似;③![]() 的长为
的长为![]() :④若
:④若![]() 分别为线段
分别为线段![]() 上的动点(不包含端点),则
上的动点(不包含端点),则![]() 的最小值是
的最小值是![]() .其中正确结论的序号是__________.
.其中正确结论的序号是__________.
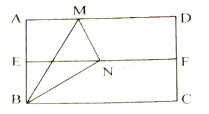
【答案】①②④
【解析】
①如图,连接AN,根据线段垂直平分线的性质得到AN=BN,根据折叠的性质得到AB=BN,推理出△ABN为等边三角形,得到∠ABN=60°,于是得到∠ABM=∠MBN=∠CBN=30°,即结论①正确;
②根据折叠的性质,可得∠BNM=∠BAD=90°,∠BEN=∠AEN=90°,根据相似三角形的判定定理得到△BEN与△BMN相似,即结论②正确;
③解直角三角形得到MN=![]() BN=
BN=![]() ,即结论③错误;
,即结论③错误;
④过A作AQ⊥BN于Q交BM于P,则此时PN+PQ的值最小,且PN+PQ=AQ,解直角三角形得到PN+PQ的最小值是![]() .即结论④正确.
.即结论④正确.
解:①如图,连接AN,
∵EF垂直平分AB,∴AN=BN,
根据折叠的性质,可得AB=BN,
∴AN=AB=BN=2.
∴△ABN为等边三角形,
∴∠ABN=60°,
∴∠ABM=∠MBN=∠CBN=30°,
即结论①正确;
②根据折叠的性质,可得∠BNM=∠BAD=90°,∠BEN=∠AEN=90°,
∴∠BEN=∠BNM,
∵∠MBN=30°,∠EBN=60°,∴∠BMN=60°,
∴∠EBN=∠BMN,
∴△BEN与△BMN相似,
即结论②正确;
③∵∠ABM=∠MBN=30°,BN=AB=2,∠BNM=∠BAM=90°,
∴MN=![]() BN=
BN=![]() ,即结论③错误;
,即结论③错误;
④∵A点和N点关于BM对称,
∴过A点作![]() 于Q交BM于P,
于Q交BM于P,
此时PN+PQ的值最小,且PN+PQ=AQ,
∵∠ABQ=60°,AB=2,
∴AQ=![]() AB=
AB=![]() ,
,
∴PN+PQ的最小值是![]() .
.
即结论④正确.
故答案为①②④.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步500m,先到终点
的人原地休息.已知甲先出发2s.在跑步过程中,甲、乙两人的距离y(m)与乙出发的时间t(s)之间的关系
如图所示,给出以下结论:①a=8;②b=92;③c=123.其中正确的是【 】

A.①②③ B.仅有①② C.仅有①③ D.仅有②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+3(a≠0)的对称轴为直线x=﹣1,抛物线交x轴于A、C两点,与直线y=x﹣1交于A、B两点,直线AB与抛物线的对称轴交于点E.
(1)求抛物线的解板式.
(2)点P在直线AB上方的抛物线上运动,若△ABP的面积最大,求此时点P的坐标.
(3)在平面直角坐标系中,以点B、E、C、D为顶点的四边形是平行四边形,请直接写出符合条件点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在![]() 中,
中,![]() 的角平分线
的角平分线![]() 交
交![]() 边于
边于![]() .
.
(1)以![]() 边上一点
边上一点![]() 为圆心,过
为圆心,过![]() 两点作
两点作![]() (不写作法,保留作图痕迹),再判断直线
(不写作法,保留作图痕迹),再判断直线![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)若(1)中的![]() 与
与![]() 边的另一个交点为
边的另一个交点为![]() ,
,![]() ,求线段
,求线段![]() 与劣弧
与劣弧![]() 所围成的图形面积.(结果保留根号和
所围成的图形面积.(结果保留根号和![]() )
)
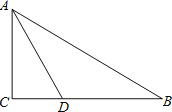
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司生产的一种产品按照质量由高到低分为A,B,C,D四级,为了增加产量、提高质量,该公司改进了一次生产工艺,使得生产总量增加了一倍.为了解新生产工艺的效果,对改进生产工艺前、后的四级产品的占比情况进行了统计,绘制了如下扇形图:
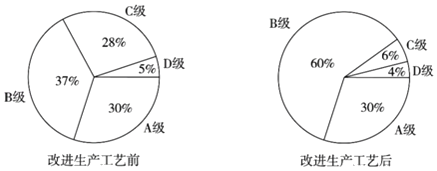
根据以上信息,下列推断合理的是( )
A.改进生产工艺后,A级产品的数量没有变化
B.改进生产工艺后,B级产品的数量增加了不到一倍
C.改进生产工艺后,C级产品的数量减少
D.改进生产工艺后,D级产品的数量减少
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为□ABCD的对称中心,点A的坐标为(-2,-2),AB=5,AB//x轴,反比例函数y=![]() 的图象经过点D,将□ABCD沿y轴向下平移,使点C的对应点C′落在反比例函数的图象上,则平移过程中线段AC扫过的面积为( )
的图象经过点D,将□ABCD沿y轴向下平移,使点C的对应点C′落在反比例函数的图象上,则平移过程中线段AC扫过的面积为( )
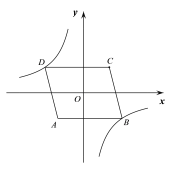
A.10B.18C.20D.24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,二次函数y=ax2+bx+c(a≠0)的图象如图所示,现给以下结论:①abc<0;②c+2a<0;③9a﹣3b+c=0;④a﹣b≥m(am+b)(m为实数);⑤4ac﹣b2<0.其中错误结论的个数有( )
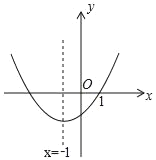
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
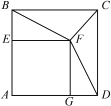
【题目】如图,正方形AEFG的顶点E、G在正方形ABCD的边AB、AD上,连接BF、DF.
![]() (1)求证:BF=DF;
(1)求证:BF=DF;
(2)连接CF,请直接写出![]() 的值为__________(不必写出计算过程).
的值为__________(不必写出计算过程).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com