
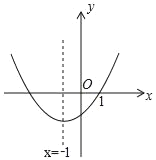
【题目】在平面直角坐标系中,二次函数y=ax2+bx+c(a≠0)的图象如图所示,现给以下结论:①abc<0;②c+2a<0;③9a﹣3b+c=0;④a﹣b≥m(am+b)(m为实数);⑤4ac﹣b2<0.其中错误结论的个数有( )
A.1个B.2个C.3个D.4个
【答案】A
【解析】
由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
解:①由抛物线可知:a>0,c<0,
对称轴x=﹣![]() <0,
<0,
∴b>0,
∴abc<0,故①正确;
②由对称轴可知:﹣![]() =﹣1,
=﹣1,
∴b=2a,
∵x=1时,y=a+b+c=0,
∴c+3a=0,
∴c+2a=﹣3a+2a=﹣a<0,故②正确;
③(1,0)关于x=﹣1的对称点为(﹣3,0),
∴x=﹣3时,y=9a﹣3b+c=0,故③正确;
④当x=﹣1时,y的最小值为a﹣b+c,
∴x=m时,y=am2+bm+c,
∴am2+bm+c≥a-b+c,
即a﹣b≤m(am+b),故④错误;
⑤抛物线与x轴有两个交点,
∴△>0,
即b2﹣4ac>0,
∴4ac﹣b2<0,故⑤正确;
故选:A.



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】“一村一品,绽放致富梦”,泰顺县恩代洋村因猕猴桃被入选全国“一村一品”示范村镇.为更新果树品种,恩代洋村某果农计划购进![]() 、
、![]() 、
、![]() 三种果树苗木栽植培育.已知
三种果树苗木栽植培育.已知![]() 种果苗每捆比
种果苗每捆比![]() 种果苗每捆多10元,
种果苗每捆多10元,![]() 种果苗每捆30元,购买50捆
种果苗每捆30元,购买50捆![]() 种果苗所花钱比购买60捆
种果苗所花钱比购买60捆![]() 种果苗的钱多100元.(每种果苗按整捆购买,且每捆果苗数相同)
种果苗的钱多100元.(每种果苗按整捆购买,且每捆果苗数相同)
(1)![]() 、
、![]() 种果苗每捆分别需要多少钱;
种果苗每捆分别需要多少钱;
(2)现批发商推出限时赠送优惠活动:购买一捆![]() 种果苗赠送一捆
种果苗赠送一捆![]() 种果苗.(最多赠送10捆
种果苗.(最多赠送10捆![]() 种果苗)
种果苗)
①若购买![]() 种果苗7捆、
种果苗7捆、![]() 种果苗5捆和
种果苗5捆和![]() 种果苗10捆,共需多少钱;
种果苗10捆,共需多少钱;
②若需购买![]() 种果苗10捆,预算资金为600元,在不超额的前提下,最多可以买多少捆果苗.求所有满足条件的方案,并指出哪种方案购买费用最少.(每种至少各1捆)
种果苗10捆,预算资金为600元,在不超额的前提下,最多可以买多少捆果苗.求所有满足条件的方案,并指出哪种方案购买费用最少.(每种至少各1捆)
查看答案和解析>>
科目:初中数学 来源: 题型:
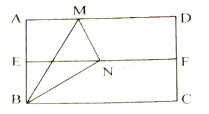
【题目】如图,在矩形纸片![]() 中,
中,![]() ,对折矩形纸片
,对折矩形纸片![]() ,使
,使![]() 与
与![]() 重合,折痕为
重合,折痕为![]() ,展平后再过点
,展平后再过点![]() 折叠,使点
折叠,使点![]() 落在
落在![]() 上的点
上的点![]() ,折痕为
,折痕为![]() .再次展平,连接
.再次展平,连接![]() ,
,![]() ,有下列结论:①
,有下列结论:①![]() ;②
;②![]() 与
与![]() 相似;③
相似;③![]() 的长为
的长为![]() :④若
:④若![]() 分别为线段
分别为线段![]() 上的动点(不包含端点),则
上的动点(不包含端点),则![]() 的最小值是
的最小值是![]() .其中正确结论的序号是__________.
.其中正确结论的序号是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着生活节奏的加快以及智能手机的普及,外卖点餐逐渐成为越来越多用户的餐饮消费习惯.由此催生了一批外卖点餐平台,已知某外卖平台的送餐费用与送餐距离有关(该平台只给5千米范围内配送),为调査送餐员的送餐收入,现从该平台随机抽取80名点外卖的用户进行统计,按送餐距离分类统计结果如下表:
送餐距离x(千米) | 0 | 1 | 2 | 3 | 4 |
数量 | 12 | 20 | 24 | 16 | 8 |
(1)从这80名点外卖的用户中任取一名用户,该用户的送餐距离不超过3千米的概率为 ;
(2)以这80名用户送餐距离为样本,同一组数据取该小组数据的中间值(例如第二小组(1<x ≤2)的中间值是1.5),试估计利用该平台点外卖用户的平均送餐距离;
(3)若该外卖平台给送餐员的送餐费用与送餐距离有关,不超过2千米时,每份3元;超过2千米但不超4千米时,每份5元;超过4千米时,每份9元. 以给这80名用户所需送餐费用的平均数为依据,若送餐员一天的目标收入不低于150元,试估计一天至少要送多少份外卖?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了强化学生的环保意识,某校团委在全校举办了“保护环境,人人有责”知识竞赛活动,初、高中根据初赛成绩,各选出5名选手组成初中代表队和高中代表队进行复赛,两个队学生的复赛成绩(满分10分)如图所示:
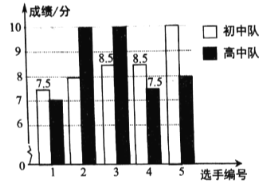
(1)根据图示填写下表:
平均分 | 中位数 | 众数 | 方差 | |
初中队 | 8.5 | 0.7 | ||
高中队 | 8.5 | 10 |
(2)小明同学说:“这次复赛我得了8分,在我们队中排名属中游偏下!”小明是初中队还是高中队的学生?为什么?
(3)结合两队成绩的平均分、中位数和方差,分析哪个对的复赛成绩较好.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:
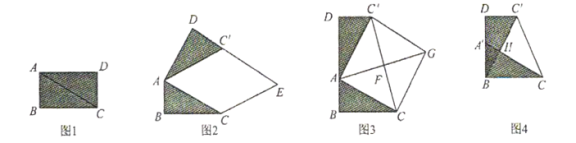
在综合与实践课上,老师让同学们以“矩形纸片的剪拼”为主题开展数学活动.如图1,将矩形纸片![]() 沿对角线
沿对角线![]() 剪开,得到
剪开,得到![]() 和
和![]() .并且量得
.并且量得![]() ,
,![]() .
.
操作发现:
(1)将图1中的![]() 以点
以点![]() 为旋转中心,按逆时针方向旋转
为旋转中心,按逆时针方向旋转![]() ,使
,使![]() ,得到如图2所示的
,得到如图2所示的![]() ,过点
,过点![]() 作
作![]() 的平行线,与
的平行线,与![]() 的延长线交于点
的延长线交于点![]() ,则四边形
,则四边形![]() 的形状是________.
的形状是________.
(2)创新小组将图1中的![]() 以点
以点![]() 为旋转中心,按逆时针方向旋转,使
为旋转中心,按逆时针方向旋转,使![]() 、
、![]() 、
、![]() 三点在同一条直线上,得到如图3所示的
三点在同一条直线上,得到如图3所示的![]() ,连接
,连接![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() 并延长至点
并延长至点![]() ,使
,使![]() ,连接
,连接![]() 、
、![]() ,得到四边形
,得到四边形![]() ,发现它是正方形,请你证明这个结论.
,发现它是正方形,请你证明这个结论.
实践探究:
(3)缜密小组在创新小组发现结论的基础上,进行如下操作:将![]() 沿着
沿着![]() 方向平移,使点
方向平移,使点![]() 与点
与点![]() 重合,此时
重合,此时![]() 点平移至
点平移至![]() 点,
点,![]() 与
与![]() 相交于点
相交于点![]() ,如图4所示,连接
,如图4所示,连接![]() ,试求
,试求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请认真阅读下面的数学探究,并完成所提出的问题.
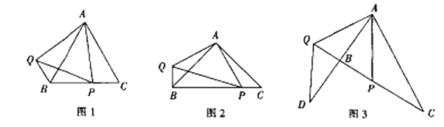
(1)探究1:如图1,在边长为![]() 的等边三角形
的等边三角形![]() 中,
中,![]() 是
是![]() 边上任意一点,连接
边上任意一点,连接![]() ,将
,将![]() 绕点
绕点![]() 按顺时针方向旋转至
按顺时针方向旋转至![]() 处,连接
处,连接![]() ,求
,求![]() 面积的最小值.
面积的最小值.
(2)探究2:如图2,若![]() 是腰长为
是腰长为![]() 的等腰直角三角形,
的等腰直角三角形,![]() ,(1)中的其他条件不变,请求出此时
,(1)中的其他条件不变,请求出此时![]() 面积的最小值.
面积的最小值.
(3)探究3:如图3,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 边上任意一点,连接
边上任意一点,连接![]() ,将
,将![]() 绕点
绕点![]() 按顺时针方向旋转至
按顺时针方向旋转至![]() 处,
处,![]() 、
、![]() 、
、![]() 三点共线,连接
三点共线,连接![]() ,求
,求![]() 的面积的最小值.
的面积的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,∠BAC的平分线交BC于点D,E为AB上的一点,DE=DC,以D为圆心,DB长为半径作⊙D,AB=5,EB=3.
(1)求证:AC是⊙D的切线;
(2)求线段AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实行垃圾分类和垃圾资源化利用,关系广大人民群众生活环境,关系节约使用资源,也是社会文明水平的一个重要体现.某环保公司研发了甲、乙两种智能设备,可利用最新技术将干垃圾进行分选破碎制成固化成型燃料棒,干垃圾由此变身新型清洁燃料.某垃圾处理厂从环保公司购入以上两种智能设备若干,已知购买甲型智能设备花费![]() 万元,购买乙型智能设备花费
万元,购买乙型智能设备花费![]() 万元,购买的两种设备数量相同,且两种智能设备的单价和为
万元,购买的两种设备数量相同,且两种智能设备的单价和为![]() 万元.
万元.
![]() 求甲、乙两种智能设备单价;
求甲、乙两种智能设备单价;
![]() 垃圾处理厂利用智能设备生产燃料棒,并将产品出售.已知燃料棒的成本由人力成本和物资成本两部分组成,其中物资成本占总成本的
垃圾处理厂利用智能设备生产燃料棒,并将产品出售.已知燃料棒的成本由人力成本和物资成本两部分组成,其中物资成本占总成本的![]() ,且生产每吨燃料棒所需人力成本比物资成本的倍
,且生产每吨燃料棒所需人力成本比物资成本的倍![]() 还多
还多![]() 元.调查发现,若燃料棒售价为每吨
元.调查发现,若燃料棒售价为每吨![]() 元,平均每天可售出
元,平均每天可售出![]() 吨,而当销售价每降低
吨,而当销售价每降低![]() 元,平均每天可多售出
元,平均每天可多售出![]() 吨.垃圾处理厂想使这种燃料棒的销售利润平均每天达到
吨.垃圾处理厂想使这种燃料棒的销售利润平均每天达到![]() 元,且保证售价在每吨
元,且保证售价在每吨![]() 元基础上降价幅度不超过
元基础上降价幅度不超过![]() ,求每吨燃料棒售价应为多少元?
,求每吨燃料棒售价应为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com