
ЎҫМвДҝЎҝЎ°Т»ҙеТ»Ж·Ј¬ХА·ЕЦВё»ГОЎұЈ¬М©ЛіПШ¶чҙъСуҙеТтвЁәпМТұ»ИлСЎИ«№ъЎ°Т»ҙеТ»Ж·ЎұКҫ·¶ҙеХтЈ®ОӘёьРВ№ыКчЖ·ЦЦЈ¬¶чҙъСуҙеДі№ыЕ©јЖ»®№әҪш![]() Ўў
Ўў![]() Ўў
Ўў![]() ИэЦЦ№ыКчГзДҫФФЦІЕаУэЈ®ТСЦӘ
ИэЦЦ№ыКчГзДҫФФЦІЕаУэЈ®ТСЦӘ![]() ЦЦ№ыГзГҝАҰұИ
ЦЦ№ыГзГҝАҰұИ![]() ЦЦ№ыГзГҝАҰ¶а10ФӘЈ¬
ЦЦ№ыГзГҝАҰ¶а10ФӘЈ¬![]() ЦЦ№ыГзГҝАҰ30ФӘЈ¬№әВт50АҰ
ЦЦ№ыГзГҝАҰ30ФӘЈ¬№әВт50АҰ![]() ЦЦ№ыГзЛщ»ЁЗ®ұИ№әВт60АҰ
ЦЦ№ыГзЛщ»ЁЗ®ұИ№әВт60АҰ![]() ЦЦ№ыГзөДЗ®¶а100ФӘЈ®ЈЁГҝЦЦ№ыГз°ҙХыАҰ№әВтЈ¬ЗТГҝАҰ№ыГзКэПаН¬Ј©
ЦЦ№ыГзөДЗ®¶а100ФӘЈ®ЈЁГҝЦЦ№ыГз°ҙХыАҰ№әВтЈ¬ЗТГҝАҰ№ыГзКэПаН¬Ј©
ЈЁ1Ј©![]() Ўў
Ўў![]() ЦЦ№ыГзГҝАҰ·ЦұрРиТӘ¶аЙЩЗ®Ј»
ЦЦ№ыГзГҝАҰ·ЦұрРиТӘ¶аЙЩЗ®Ј»
ЈЁ2Ј©ПЦЕъ·ўЙМНЖіцПЮКұФщЛНУЕ»Э»о¶ҜЈә№әВтТ»АҰ![]() ЦЦ№ыГзФщЛНТ»АҰ
ЦЦ№ыГзФщЛНТ»АҰ![]() ЦЦ№ыГзЈ®ЈЁЧо¶аФщЛН10АҰ
ЦЦ№ыГзЈ®ЈЁЧо¶аФщЛН10АҰ![]() ЦЦ№ыГзЈ©
ЦЦ№ыГзЈ©
ўЩИф№әВт![]() ЦЦ№ыГз7АҰЎў
ЦЦ№ыГз7АҰЎў![]() ЦЦ№ыГз5АҰәН
ЦЦ№ыГз5АҰәН![]() ЦЦ№ыГз10АҰЈ¬№ІРи¶аЙЩЗ®Ј»
ЦЦ№ыГз10АҰЈ¬№ІРи¶аЙЩЗ®Ј»
ўЪИфРи№әВт![]() ЦЦ№ыГз10АҰЈ¬ФӨЛгЧКҪрОӘ600ФӘЈ¬ФЪІ»і¬¶оөДЗ°МбПВЈ¬Чо¶аҝЙТФВт¶аЙЩАҰ№ыГзЈ®ЗуЛщУРВъЧгМхјюөД·Ҫ°ёЈ¬ІўЦёіцДДЦЦ·Ҫ°ё№әВт·СУГЧоЙЩЈ®ЈЁГҝЦЦЦБЙЩёч1АҰЈ©
ЦЦ№ыГз10АҰЈ¬ФӨЛгЧКҪрОӘ600ФӘЈ¬ФЪІ»і¬¶оөДЗ°МбПВЈ¬Чо¶аҝЙТФВт¶аЙЩАҰ№ыГзЈ®ЗуЛщУРВъЧгМхјюөД·Ҫ°ёЈ¬ІўЦёіцДДЦЦ·Ҫ°ё№әВт·СУГЧоЙЩЈ®ЈЁГҝЦЦЦБЙЩёч1АҰЈ©
Ўҫҙр°ёЎҝЈЁ1Ј©50ФӘЈ»40ФӘЈ»ЈЁ2Ј©ўЩ640ФӘЈ»ўЪјыҪвОц
ЎҫҪвОцЎҝ
ЈЁ1Ј©ёщҫЭМвТвЙи![]() ЦР№ыГзГҝАҰ
ЦР№ыГзГҝАҰ![]() ФӘЈ¬Фт
ФӘЈ¬Фт![]() ЦР№ыГзГҝАҰ
ЦР№ыГзГҝАҰ![]() ФӘЈ¬БРіц·ҪіМЈ¬Ҫв·ҪіМјҙҝЙөГөҪҙр°ёЈ»
ФӘЈ¬БРіц·ҪіМЈ¬Ҫв·ҪіМјҙҝЙөГөҪҙр°ёЈ»
ЈЁ2Ј©ўЩУЙМвТвЈ¬БРіцөИКҪЈ¬И»әуҪшРРјЖЛгЈ¬јҙҝЙөГөҪҙр°ёЈ»
ўЪёщҫЭМвТвЈ¬ҝЙ·ЦОӘ![]() әН
әН![]() БҪЦЦЗйҝцҪшРР·ЦОцЈ¬·ЦұрЗуіцВъЧгМхјюөД·Ҫ°ёЈ¬И»әујЖЛг·СУГјҙҝЙЈ®
БҪЦЦЗйҝцҪшРР·ЦОцЈ¬·ЦұрЗуіцВъЧгМхјюөД·Ҫ°ёЈ¬И»әујЖЛг·СУГјҙҝЙЈ®
ҪвЈәЈЁ1Ј©Йи![]() ЦР№ыГзГҝАҰ
ЦР№ыГзГҝАҰ![]() ФӘЈ¬Фт
ФӘЈ¬Фт![]() ЦР№ыГзГҝАҰ
ЦР№ыГзГҝАҰ![]() ФӘ
ФӘ
![]()
ҪвөГЈә![]()
![]() ЦЦ№ыГзГҝАҰЈә
ЦЦ№ыГзГҝАҰЈә![]() ФӘ
ФӘ
ҙрЈә![]() ЦЦ№ыГзГҝАҰ50ФӘЈ¬
ЦЦ№ыГзГҝАҰ50ФӘЈ¬![]() ЦЦ№ыГзГҝАҰ40ФӘЈ®
ЦЦ№ыГзГҝАҰ40ФӘЈ®
ЈЁ2Ј©ўЩЎЯ7АҰ![]() ЦЦ№ыГзҝЙГв·СФщЛН7АҰ
ЦЦ№ыГзҝЙГв·СФщЛН7АҰ![]() ЦЦ№ыГзЈ¬
ЦЦ№ыГзЈ¬
ЎаЛщРиЧЬ·СУГОӘЈә![]() ЈЁФӘЈ©
ЈЁФӘЈ©
ўЪҝЙЙи№әВт![]() ЦЦ№ыГз
ЦЦ№ыГз![]() АҰЈ¬
АҰЈ¬![]() ЦЦ№ыГз
ЦЦ№ыГз![]() АҰ
АҰ
өұ![]() КұЈ¬
КұЈ¬
ЈЁIЈ©өұ![]() КұЈ¬
КұЈ¬![]() Ј¬
Ј¬
Ўа![]()
Ўа![]() Ј¬ҙЛКұ
Ј¬ҙЛКұ![]() Ј¬·СУГОӘ580ФӘ
Ј¬·СУГОӘ580ФӘ
ЈЁIIЈ©өұ![]() КұЈ¬
КұЈ¬![]() Ј¬
Ј¬
Ўа![]()
Ўа![]() Ј¬ҙЛКұ
Ј¬ҙЛКұ![]() Ј¬·СУГОӘ590ФӘ
Ј¬·СУГОӘ590ФӘ
ЈЁIIIЈ©өұ![]() КұЈ¬
КұЈ¬![]() Ј¬
Ј¬
Ўа![]() Ј¬І»әПМвТвЈ¬ЙбИҘ
Ј¬І»әПМвТвЈ¬ЙбИҘ
өұ![]() КұЈ¬
КұЈ¬
ЈЁIЈ©өұ![]() КұЈ¬
КұЈ¬![]() Ј¬
Ј¬
Ўа![]()
Ўа![]() Ј¬ҙЛКұ
Ј¬ҙЛКұ![]() Ј¬·СУГОӘ600ФӘ
Ј¬·СУГОӘ600ФӘ
ЈЁIIЈ©өұ![]() КұЈ¬
КұЈ¬![]() Ј¬
Ј¬
Ўа![]()
Ўа![]() Ј¬ҙЛКұ
Ј¬ҙЛКұ![]() Ј¬І»әПМвТвЈ¬ЙбИҘ
Ј¬І»әПМвТвЈ¬ЙбИҘ
ЈЁIIIЈ©өұ![]() КұЈ¬
КұЈ¬![]() Ј¬І»әПМвТвЈ¬ЙбИҘ.
Ј¬І»әПМвТвЈ¬ЙбИҘ.
ЧЫЙПЛщКцЈ¬Чо¶аҝЙ№әВт![]() ЦЦ№ыГзәН
ЦЦ№ыГзәН![]() ЦЦ№ыГз№І12АҰЈ¬УРИэЦЦ·Ҫ°ёЈәҝЙВт
ЦЦ№ыГз№І12АҰЈ¬УРИэЦЦ·Ҫ°ёЈәҝЙВт![]() ЦЦ№ыГз9АҰЈ¬
ЦЦ№ыГз9АҰЈ¬![]() ЦЦ№ыГз3АҰЈ»
ЦЦ№ыГз3АҰЈ»![]() ЦЦ№ыГз10АҰЈ¬
ЦЦ№ыГз10АҰЈ¬![]() ЦЦ№ыГз2АҰЈ»
ЦЦ№ыГз2АҰЈ»![]() ЦЦ№ыГз11АҰЈ¬
ЦЦ№ыГз11АҰЈ¬![]() ЦЦ№ыГз1АҰЈ»ЖдЦРөұ
ЦЦ№ыГз1АҰЈ»ЖдЦРөұ![]() ЦЦ№ыГз10АҰЈ¬
ЦЦ№ыГз10АҰЈ¬![]() ЦЦ№ыГз2АҰКұЈ¬Лщ»Ё·СУГЧоЙЩЈ¬ОӘ580ФӘ.
ЦЦ№ыГз2АҰКұЈ¬Лщ»Ё·СУГЧоЙЩЈ¬ОӘ580ФӘ.



| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ЛДұЯРОABCDКЗЎСOөДДЪҪУЛДұЯРОЈ¬BCКЗЎСOөДЦұҫ¶Ј¬OEЎНBCҪ»ABУЪөгEЈ¬ИфBE=2AEЈ¬ФтЎПADC =_________ЎгЈ®
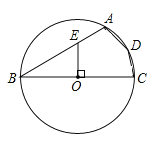
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝ·ҪіМ![]() өДёщҝЙКУОӘәҜКэ
өДёщҝЙКУОӘәҜКэ![]() өДНјПуУләҜКэ
өДНјПуУләҜКэ![]() өДНјПуҪ»өгөДәбЧшұкЈ¬Фт·ҪіМ
өДНјПуҪ»өгөДәбЧшұкЈ¬Фт·ҪіМ![]() өДКөёщ
өДКөёщ![]() ЛщФЪөД·¶О§КЗ( )
ЛщФЪөД·¶О§КЗ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝ¶ФУЪ![]() ј°Т»ёцҫШРОёшіцИзПВ¶ЁТеЈәИз№ы
ј°Т»ёцҫШРОёшіцИзПВ¶ЁТеЈәИз№ы![]() ЙПҙжФЪөҪҙЛҫШРОЛД·Э¶ҘөгҫаАл¶јПаөИөДөгЈ¬ДЗГҙіЖ
ЙПҙжФЪөҪҙЛҫШРОЛД·Э¶ҘөгҫаАл¶јПаөИөДөгЈ¬ДЗГҙіЖ![]() КЗёГҫШРОөДЎ°өИҫаФІЎұЈ¬ИзНјЈ¬ЖҪГжЦұҪЗЧшұкПө
КЗёГҫШРОөДЎ°өИҫаФІЎұЈ¬ИзНјЈ¬ЖҪГжЦұҪЗЧшұкПө![]() ЦРЈ¬ҫШРО
ЦРЈ¬ҫШРО![]() өД¶Ҙөг
өД¶Ҙөг![]() ЧшұкОӘ
ЧшұкОӘ![]() Ј¬¶Ҙөг
Ј¬¶Ҙөг![]() ФЪ
ФЪ![]() ЦбЙПЈ¬
ЦбЙПЈ¬![]() Ј¬ЗТ
Ј¬ЗТ![]() өД°лҫ¶ОӘ
өД°лҫ¶ОӘ![]() Ј®
Ј®
ЈЁ1Ј©ФЪ![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() ЦРҝЙТФіЙОӘҫШРО
ЦРҝЙТФіЙОӘҫШРО![]() өДЎ°өИҫаФІЎұөДФІРДөДКЗ__________Ј®
өДЎ°өИҫаФІЎұөДФІРДөДКЗ__________Ј®
ЈЁ2Ј©Из№ыөг![]() ФЪЦұПЯ
ФЪЦұПЯ![]() ЙПЈ¬ЗТ
ЙПЈ¬ЗТ![]() КЗҫШРОөДЎ°өИҫаФІЎұЈ¬ДЗГҙөг
КЗҫШРОөДЎ°өИҫаФІЎұЈ¬ДЗГҙөг![]() өДЧшұкОӘ__________Ј®
өДЧшұкОӘ__________Ј®
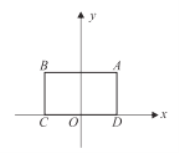
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝЈЁ1Ј©ОКМв·ўПЦ
ИзНј1Ј¬ФЪЎчOABәНЎчOCDЦРЈ¬OA=OBЈ¬OC=ODЈ¬ЎПAOB=ЎПCOD=40ЎгЈ¬Б¬ҪУACЈ¬BDҪ»УЪөгMЈ®МоҝХЈә
ўЩ![]() өДЦөОӘЎЎ ЎЎЈ»
өДЦөОӘЎЎ ЎЎЈ»
ўЪЎПAMBөД¶ИКэОӘЎЎ ЎЎЈ®
ЈЁ2Ј©АаұИМҪҫҝ
ИзНј2Ј¬ФЪЎчOABәНЎчOCDЦРЈ¬ЎПAOB=ЎПCOD=90ЎгЈ¬ЎПOAB=ЎПOCD=30ЎгЈ¬Б¬ҪУACҪ»BDөДСУіӨПЯУЪөгMЈ®ЗлЕР¶П![]() өДЦөј°ЎПAMBөД¶ИКэЈ¬ІўЛөГчАнУЙЈ»
өДЦөј°ЎПAMBөД¶ИКэЈ¬ІўЛөГчАнУЙЈ»
ЈЁ3Ј©НШХ№СУЙм
ФЪЈЁ2Ј©өДМхјюПВЈ¬Ҫ«ЎчOCDИЖөгOФЪЖҪГжДЪРэЧӘЈ¬ACЈ¬BDЛщФЪЦұПЯҪ»УЪөгMЈ¬ИфOD=1Ј¬OB=![]() Ј¬ЗлЦұҪУРҙіцөұөгCУлөгMЦШәПКұACөДіӨЈ®
Ј¬ЗлЦұҪУРҙіцөұөгCУлөгMЦШәПКұACөДіӨЈ®

Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝДіДіУГ»§ЕаУэБЛјЧТТБҪЦЦ·¬ЗСЈ¬ёчЛж»ъійИЎБЛ10ҝГУЧГзЈ¬ІвКФёЯ¶ИИзПВЈЁөҘО»ЈәcmЈ©
јЧЈә10Ј¬9Ј¬10Ј¬10Ј¬13Ј¬8Ј¬7Ј¬12Ј¬10Ј¬11
ТТЈә9Ј¬10Ј¬8Ј¬11Ј¬10Ј¬11Ј¬10Ј¬9Ј¬10Ј¬12
ДгИПОӘДДЦЦ·¬ЗСіӨөГұИҪПХыЖлЈҝЗлЛөГчАнУЙ.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝјЧЎўТТБҪИЛФЪЦұПЯЕЬөАЙПН¬ЖрөгЎўН¬ЦХөгЎўН¬·ҪПтФИЛЩЕЬІҪ500mЈ¬ПИөҪЦХөг
өДИЛФӯөШРЭПўЈ®ТСЦӘјЧПИіц·ў2sЈ®ФЪЕЬІҪ№эіМЦРЈ¬јЧЎўТТБҪИЛөДҫаАлy(m)УлТТіц·ўөДКұјдt(s)Ц®јдөД№ШПө
ИзНјЛщКҫЈ¬ёшіцТФПВҪбВЫЈәўЩaЈҪ8Ј»ўЪbЈҪ92Ј»ўЫcЈҪ123Ј®ЖдЦРХэИ·өДКЗЎҫ Ўҝ

AЈ®ўЩўЪўЫ BЈ®ҪцУРўЩўЪ CЈ®ҪцУРўЩўЫ DЈ®ҪцУРўЪўЫ
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ЕЧОпПЯyЈҪax2+bx+3(aЎЩ0)өД¶ФіЖЦбОӘЦұПЯxЈҪ©Ғ1Ј¬ЕЧОпПЯҪ»xЦбУЪAЎўCБҪөгЈ¬УлЦұПЯyЈҪx©Ғ1Ҫ»УЪAЎўBБҪөгЈ¬ЦұПЯABУлЕЧОпПЯөД¶ФіЖЦбҪ»УЪөгEЈ®
(1)ЗуЕЧОпПЯөДҪв°еКҪЈ®
(2)өгPФЪЦұПЯABЙП·ҪөДЕЧОпПЯЙПФЛ¶ҜЈ¬ИфЎчABPөДГж»эЧоҙуЈ¬ЗуҙЛКұөгPөДЧшұкЈ®
(3)ФЪЖҪГжЦұҪЗЧшұкПөЦРЈ¬ТФөгBЎўEЎўCЎўDОӘ¶ҘөгөДЛДұЯРОКЗЖҪРРЛДұЯРОЈ¬ЗлЦұҪУРҙіц·ыәПМхјюөгDөДЧшұкЈ®

Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝФЪЖҪГжЦұҪЗЧшұкПөЦРЈ¬¶юҙОәҜКэyЈҪax2+bx+cЈЁaЎЩ0Ј©өДНјПуИзНјЛщКҫЈ¬ПЦёшТФПВҪбВЫЈәўЩabcЈј0Ј»ўЪc+2aЈј0Ј»ўЫ9a©Ғ3b+cЈҪ0Ј»ўЬa©ҒbЎЭmЈЁam+bЈ©ЈЁmОӘКөКэЈ©Ј»ўЭ4ac©Ғb2Јј0Ј®ЖдЦРҙнОуҪбВЫөДёцКэУРЈЁЎЎЎЎЈ©
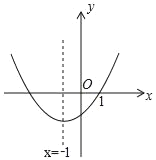
A.1ёцB.2ёцC.3ёцD.4ёц
Ійҝҙҙр°ёәНҪвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com