
【题目】对于![]() 及一个矩形给出如下定义:如果
及一个矩形给出如下定义:如果![]() 上存在到此矩形四份顶点距离都相等的点,那么称
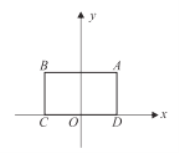
上存在到此矩形四份顶点距离都相等的点,那么称![]() 是该矩形的“等距圆”,如图,平面直角坐标系
是该矩形的“等距圆”,如图,平面直角坐标系![]() 中,矩形
中,矩形![]() 的顶点
的顶点![]() 坐标为
坐标为![]() ,顶点
,顶点![]() 在
在![]() 轴上,
轴上,![]() ,且
,且![]() 的半径为
的半径为![]() .
.
(1)在![]() ,
,![]() ,
,![]() 中可以成为矩形
中可以成为矩形![]() 的“等距圆”的圆心的是__________.
的“等距圆”的圆心的是__________.
(2)如果点![]() 在直线
在直线![]() 上,且
上,且![]() 是矩形的“等距圆”,那么点
是矩形的“等距圆”,那么点![]() 的坐标为__________.
的坐标为__________.
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=mx2﹣2mx﹣2m+1与x轴交于点A,B.
(1)若AB=2,求m的值;
(2)过点P(0,2)作与x轴平行的直线,交抛物线于点M,N.当MN![]() 2时,求m的取值范围.
2时,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
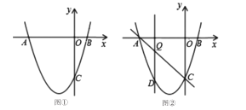
【题目】如图,抛物线![]() 交
交![]() 轴于点
轴于点![]() 和点
和点![]() ,交
,交![]() 轴于点
轴于点![]() .
.
(1)求抛物线的函数表达式;
(2)若点![]() 在抛物线上,且
在抛物线上,且![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)如图②,设点![]() 是线段
是线段![]() 上的一动点,作
上的一动点,作![]() 轴,交抛物线于点
轴,交抛物线于点![]() ,是否存在
,是否存在![]() 面积的最大值?若存在,请求出点
面积的最大值?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
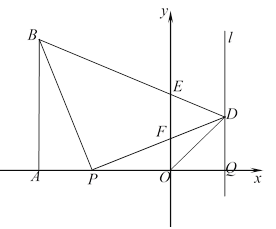
【题目】如图,在平面直角坐标系![]() 中,
中,![]()
![]() 轴于点
轴于点![]() .点
.点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度沿
个单位长度的速度沿![]() 轴向点
轴向点![]() 运动;点
运动;点![]() 从点
从点![]() 同时出发,以相同的速度沿
同时出发,以相同的速度沿![]() 轴的正方向运动,运动时间
轴的正方向运动,运动时间![]()
![]() .过点
.过点![]() 作平行于
作平行于![]() 轴的直线
轴的直线![]() ,连接
,连接![]() ,过
,过![]() 点作
点作![]() 交直线
交直线![]() 于点
于点![]() ,
,![]() 、
、![]() 与
与![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,连接
,连接![]() .
.
(1)当![]() 时,试求
时,试求![]() 的值;
的值;
(2)当![]() 为
为![]() 中点时,试求
中点时,试求![]() 的值;
的值;
(3)是否存在这样的![]() ,使得
,使得![]() 与
与![]() 的面积相等?若存在,求出所有符合条件的
的面积相等?若存在,求出所有符合条件的![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究
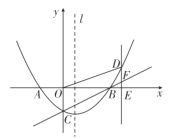
如图,抛物线![]() ,与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,抛物线的对称轴为l.
,与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,抛物线的对称轴为l.
(1)求点A,B,C的坐标;
(2)若点D是第一象限内抛物线上一点,过点D作![]() 轴于点E,交直线BC于点F,当
轴于点E,交直线BC于点F,当![]() 时,求四边形DOBF的面积;
时,求四边形DOBF的面积;
(3)在(2)的条件下,若点M在抛物线上,点N在抛物线的对称轴上,是否存在以点B,D,M,N为顶点的四边形是平行四边形?若存在,请求出所有符合条件的点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象分别交x轴、y轴于C,D两点,交反比例函数
的图象分别交x轴、y轴于C,D两点,交反比例函数![]() 图象于A(
图象于A(![]() ,4),B(3,m)两点.
,4),B(3,m)两点.
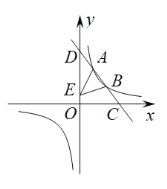
(1)求直线CD的表达式;
(2)点E是线段OD上一点,若![]() ,求E点的坐标;
,求E点的坐标;
(3)请你根据图象直接写出不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“一村一品,绽放致富梦”,泰顺县恩代洋村因猕猴桃被入选全国“一村一品”示范村镇.为更新果树品种,恩代洋村某果农计划购进![]() 、
、![]() 、
、![]() 三种果树苗木栽植培育.已知
三种果树苗木栽植培育.已知![]() 种果苗每捆比
种果苗每捆比![]() 种果苗每捆多10元,
种果苗每捆多10元,![]() 种果苗每捆30元,购买50捆
种果苗每捆30元,购买50捆![]() 种果苗所花钱比购买60捆
种果苗所花钱比购买60捆![]() 种果苗的钱多100元.(每种果苗按整捆购买,且每捆果苗数相同)
种果苗的钱多100元.(每种果苗按整捆购买,且每捆果苗数相同)
(1)![]() 、
、![]() 种果苗每捆分别需要多少钱;
种果苗每捆分别需要多少钱;
(2)现批发商推出限时赠送优惠活动:购买一捆![]() 种果苗赠送一捆
种果苗赠送一捆![]() 种果苗.(最多赠送10捆
种果苗.(最多赠送10捆![]() 种果苗)
种果苗)
①若购买![]() 种果苗7捆、
种果苗7捆、![]() 种果苗5捆和
种果苗5捆和![]() 种果苗10捆,共需多少钱;
种果苗10捆,共需多少钱;
②若需购买![]() 种果苗10捆,预算资金为600元,在不超额的前提下,最多可以买多少捆果苗.求所有满足条件的方案,并指出哪种方案购买费用最少.(每种至少各1捆)
种果苗10捆,预算资金为600元,在不超额的前提下,最多可以买多少捆果苗.求所有满足条件的方案,并指出哪种方案购买费用最少.(每种至少各1捆)
查看答案和解析>>
科目:初中数学 来源: 题型:
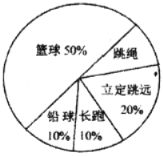
【题目】九年级(1)班学生在完成课题学习“体质健康测试中的数据分析”后,利用课外活动时间积极参加体育锻炼,每位同学从篮球、跳绳、立定跳远、长跑、铅球中选一项进行训练,训练后都进行了测试.现将项目选择情况及训练后篮球定时定点投篮测试成绩整理后作出如下统计图.请你根据上面提供的信息回答下列问题:
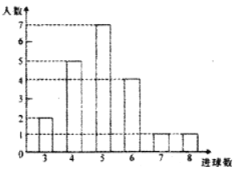
(1)该班共有学生______人,训练后篮球定时定点投篮平均每个人的进球数是_______.
(2)老师决定从选择铅球训练的![]() 名男生和
名男生和![]() 名女生中任选两名学生先进行测试,请用列表或画树形图的方法求恰好选中两名男生的概率.
名女生中任选两名学生先进行测试,请用列表或画树形图的方法求恰好选中两名男生的概率.
项目选择人数情况统计图
训练后篮球定时定点投篮测试进球数统计图
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着生活节奏的加快以及智能手机的普及,外卖点餐逐渐成为越来越多用户的餐饮消费习惯.由此催生了一批外卖点餐平台,已知某外卖平台的送餐费用与送餐距离有关(该平台只给5千米范围内配送),为调査送餐员的送餐收入,现从该平台随机抽取80名点外卖的用户进行统计,按送餐距离分类统计结果如下表:
送餐距离x(千米) | 0 | 1 | 2 | 3 | 4 |
数量 | 12 | 20 | 24 | 16 | 8 |
(1)从这80名点外卖的用户中任取一名用户,该用户的送餐距离不超过3千米的概率为 ;
(2)以这80名用户送餐距离为样本,同一组数据取该小组数据的中间值(例如第二小组(1<x ≤2)的中间值是1.5),试估计利用该平台点外卖用户的平均送餐距离;
(3)若该外卖平台给送餐员的送餐费用与送餐距离有关,不超过2千米时,每份3元;超过2千米但不超4千米时,每份5元;超过4千米时,每份9元. 以给这80名用户所需送餐费用的平均数为依据,若送餐员一天的目标收入不低于150元,试估计一天至少要送多少份外卖?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com