
����Ŀ�������������ļӿ��Լ������ֻ����ռ������������ΪԽ��Խ���û��IJ�������ϰ�ߣ��ɴ˴�����һ���������ƽ̨����֪ij����ƽ̨���Ͳͷ������Ͳ;����йأ���ƽֻ̨��5ǧ��Χ�����ͣ���Ϊ�����Ͳ�Ա���Ͳ����룬�ִӸ�ƽ̨�����ȡ80�����������û�����ͳ�ƣ����Ͳ;������ͳ�ƽ�����±���
�Ͳ;���x��ǧ�ף� | 0 | 1 | 2 | 3 | 4 |
���� | 12 | 20 | 24 | 16 | 8 |
��1������80�����������û�����ȡһ���û������û����Ͳ;��벻����3ǧ�ĸ���Ϊ ��
��2������80���û��Ͳ;���Ϊ������ͬһ������ȡ��С�����ݵ��м�ֵ������ڶ�С�飨1��x ��2�����м�ֵ��1.5�����Թ������ø�ƽ̨�������û���ƽ���Ͳ;��룻
��3����������ƽ̨���Ͳ�Ա���Ͳͷ������Ͳ;����йأ�������2ǧ��ʱ��ÿ��3Ԫ������2ǧ������4ǧ��ʱ��ÿ��5Ԫ������4ǧ��ʱ��ÿ��9Ԫ�� �Ը���80���û������Ͳͷ��õ�ƽ����Ϊ���ݣ����Ͳ�Աһ���Ŀ�����벻����150Ԫ���Թ���һ������Ҫ�Ͷ��ٷ�������
���𰸡���1��![]() ����2���������ø�ƽ̨�������û���ƽ���Ͳ;���Ϊ2.35ǧ�ף���3������һ������Ҫ��33��������
����2���������ø�ƽ̨�������û���ƽ���Ͳ;���Ϊ2.35ǧ�ף���3������һ������Ҫ��33��������
��������
��1���ɱ������ݣ���Ƶ�ʼ�������ĸ���ֵ��
��2�������Ȩƽ�������ɣ�
��3��������һ��������ƽ�����룬�����һ������Ҫ�Ͷ��ٷ�������
��1���ɱ������ݣ���������ĸ���ΪP=![]() ��
��
�ʴ�Ϊ��![]() ��
��
��2���������ø�ƽ̨�������û���ƽ���Ͳ;���Ϊ��
![]() ����12��0.5+20��1.5+24��2.5+16��3.5+8��4.5��=2.35��ǧ�ף���
����12��0.5+20��1.5+24��2.5+16��3.5+8��4.5��=2.35��ǧ�ף���
��3����һ��������ƽ������Ϊ��3��![]() +5
+5![]() +9��
+9��![]() =
=![]() ��Ԫ����
��Ԫ����
��150��![]() ��32.6��
��32.6��
���Թ���һ������Ҫ��33��������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
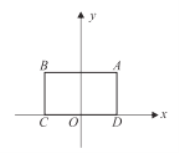
����Ŀ������![]() ��һ�����θ������¶��壺���
��һ�����θ������¶��壺���![]() �ϴ��ڵ��˾����ķݶ�����붼��ȵĵ㣬��ô��
�ϴ��ڵ��˾����ķݶ�����붼��ȵĵ㣬��ô��![]() �Ǹþ��ε����Ⱦ�Բ������ͼ��ƽ��ֱ������ϵ
�Ǹþ��ε����Ⱦ�Բ������ͼ��ƽ��ֱ������ϵ![]() �У�����
�У�����![]() �Ķ���
�Ķ���![]() ����Ϊ
����Ϊ![]() ������
������![]() ��
��![]() ���ϣ�
���ϣ�![]() ����
����![]() �İ뾶Ϊ
�İ뾶Ϊ![]() ��
��
��1����![]() ��
��![]() ��
��![]() �п��Գ�Ϊ����
�п��Գ�Ϊ����![]() �����Ⱦ�Բ����Բ�ĵ���__________��
�����Ⱦ�Բ����Բ�ĵ���__________��
��2�������![]() ��ֱ��
��ֱ��![]() �ϣ���
�ϣ���![]() �Ǿ��ε����Ⱦ�Բ������ô��
�Ǿ��ε����Ⱦ�Բ������ô��![]() ������Ϊ__________��
������Ϊ__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y��ax2+bx+3(a��0)�ĶԳ���Ϊֱ��x����1�������߽�x����A��C���㣬��ֱ��y��x��1����A��B���㣬ֱ��AB�������ߵĶԳ��ύ�ڵ�E��
(1)�������ߵĽ��ʽ��
(2)��P��ֱ��AB�Ϸ������������˶�������ABP�����������ʱ��P�����꣮
(3)��ƽ��ֱ������ϵ�У��Ե�B��E��C��DΪ������ı�����ƽ���ı��Σ���ֱ��д������������D�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾������һ�ֲ�Ʒ���������ɸߵ��ͷ�ΪA��B��C��D�ļ���Ϊ�����Ӳ���������������ù�˾�Ľ���һ���������գ�ʹ����������������һ����Ϊ�˽����������յ�Ч�����ԸĽ���������ǰ������ļ���Ʒ��ռ�����������ͳ�ƣ���������������ͼ��
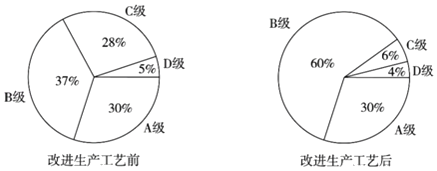
����������Ϣ�������ƶϺ������ǣ�������
A.�Ľ��������պ�A����Ʒ������û�б仯
B.�Ľ��������պ�B����Ʒ�����������˲���һ��
C.�Ľ��������պ�C����Ʒ����������
D.�Ľ��������պ�D����Ʒ����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�OΪ��ABCD�ĶԳ����ģ���A������Ϊ(��2����2)��AB=5��AB//x�ᣬ����������y=![]() ��ͼ����D������ABCD��y������ƽ�ƣ�ʹ��C�Ķ�Ӧ��C�����ڷ�����������ͼ���ϣ���ƽ�ƹ������߶�ACɨ�������Ϊ(����)
��ͼ����D������ABCD��y������ƽ�ƣ�ʹ��C�Ķ�Ӧ��C�����ڷ�����������ͼ���ϣ���ƽ�ƹ������߶�ACɨ�������Ϊ(����)
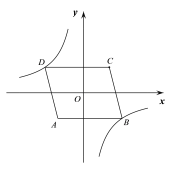
A.10B.18C.20D.24
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
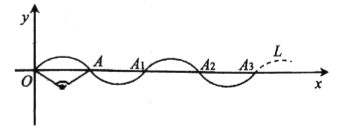
����Ŀ������![]() ��ֱ������ϵ�е�λ����ͼ��ʾ������
��ֱ������ϵ�е�λ����ͼ��ʾ������![]() ���ɰ뾶Ϊ2��Բ�Ľ�Ϊ
���ɰ뾶Ϊ2��Բ�Ľ�Ϊ![]() ��
��![]() ��
��![]() ������ԭ�㣬��
������ԭ�㣬��![]() ��
��![]() ���ϣ��Ƶ�
���ϣ��Ƶ�![]() ��ת
��ת![]() ���õ�
���õ�![]() ���ٽ�
���ٽ�![]() �Ƶ�
�Ƶ�![]() ��ת
��ת![]() ���õ�
���õ�![]() �������������ƣ��γ�����
�������������ƣ��γ�����![]() ������һ��
������һ��![]() ��
��![]() ���������ÿ��
���������ÿ��![]() ����λ���ȵ��ٶȣ�������
����λ���ȵ��ٶȣ�������![]() �����˶������
�����˶������![]() ������Ϊ___________���ڵ�
������Ϊ___________���ڵ�![]() ʱ����
ʱ����![]() ������Ϊ____________��
������Ϊ____________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У����κ���y��ax2+bx+c��a��0����ͼ����ͼ��ʾ���ָ����½��ۣ���abc��0����c+2a��0����9a��3b+c��0����a��b��m��am+b����mΪʵ��������4ac��b2��0�����д�����۵ĸ����У�������
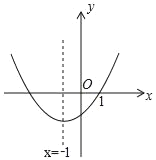
A.1��B.2��C.3��D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�ı���![]() �У�
��![]() ��
��![]() �ֱ���
�ֱ���![]() ��
��![]() ���ϵĵ㣬
���ϵĵ㣬![]() ��
��![]() ���ڵ�
���ڵ�![]() .
.
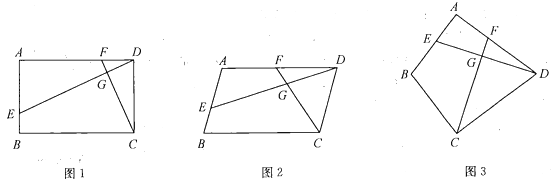
��1����ͼ1�����ı���![]() �Ǿ��Σ���
�Ǿ��Σ���![]() ����֤��
����֤��![]() ��
��
��2����ͼ2�����ı���![]() ��ƽ���ı��Σ���̽������
��ƽ���ı��Σ���̽������![]() ��
��![]() ����ʲô��ϵʱ��ʹ��
����ʲô��ϵʱ��ʹ��![]() ��������֤����Ľ��ۣ�
��������֤����Ľ��ۣ�
��3����ͼ3����![]() ��
��![]() ��
��![]() ��
��![]() ����ֱ��д��
����ֱ��д��![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ���![]() ��ͼ����
��ͼ����![]() �ύ�ڵ�
�ύ�ڵ�![]() ��
��![]() ����
����![]() λ�ڶԳ������ࣩ����
λ�ڶԳ������ࣩ����![]() �ύ�ڵ�
�ύ�ڵ�![]() .��
.��![]() Ϊ�߶�
Ϊ�߶�![]() ��һ�㣬����
��һ�㣬����![]() ��ֱ��
��ֱ��![]() �ύͼ���ڵ�
�ύͼ���ڵ�![]() ��
��![]() ����
����![]() �ڵ�
�ڵ�![]() ����ࣩ����
����ࣩ����![]() .
.
��1����ö��κ����ĶԳ��ἰ![]() ��ֵ.
��ֵ.
��2��������![]() ����ƽ��
����ƽ��![]() ����λ����
����λ����![]() ���ٹ���
���ٹ���![]() ��ֱ��
��ֱ��![]() �ĶԳƵ�
�ĶԳƵ�![]() ������
������![]() ��
��![]() ���Ϸ���ͼ����һ���ҵ�
���Ϸ���ͼ����һ���ҵ�![]() �����Ϊ1����
�����Ϊ1����![]() ��
��![]() ��ֵ.
��ֵ.
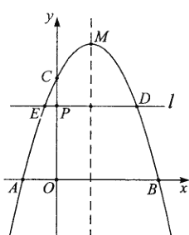
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com