
【题目】曲线![]() 在直角坐标系中的位置如图所示,曲线
在直角坐标系中的位置如图所示,曲线![]() 是由半径为2,圆心角为
是由半径为2,圆心角为![]() 的
的![]() (
(![]() 是坐标原点,点
是坐标原点,点![]() 在
在![]() 轴上)绕点
轴上)绕点![]() 旋转
旋转![]() ,得到
,得到![]() ;再将
;再将![]() 绕点
绕点![]() 旋转
旋转![]() ,得到
,得到![]() ;……依次类推,形成曲线
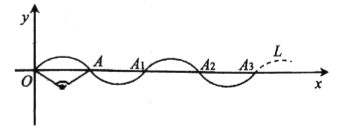
;……依次类推,形成曲线![]() ,现有一点
,现有一点![]() 从
从![]() 点出发,以每秒
点出发,以每秒![]() 个单位长度的速度,沿曲线
个单位长度的速度,沿曲线![]() 向右运动,则点
向右运动,则点![]() 的坐标为___________;在第
的坐标为___________;在第![]() 时,点
时,点![]() 的坐标为____________.
的坐标为____________.
 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象分别交x轴、y轴于C,D两点,交反比例函数
的图象分别交x轴、y轴于C,D两点,交反比例函数![]() 图象于A(
图象于A(![]() ,4),B(3,m)两点.
,4),B(3,m)两点.
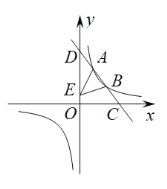
(1)求直线CD的表达式;
(2)点E是线段OD上一点,若![]() ,求E点的坐标;
,求E点的坐标;
(3)请你根据图象直接写出不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划购进![]() 、
、![]() 两种新型节能台灯共
两种新型节能台灯共![]() 盏,这两种台灯的进价、售价如表所示:
盏,这两种台灯的进价、售价如表所示:

(![]() )若商场预计进货款为
)若商场预计进货款为![]() 元,则这两种台灯各购进多少盏?
元,则这两种台灯各购进多少盏?
(![]() )若商场规定
)若商场规定![]() 型台灯的进货数量不超过
型台灯的进货数量不超过![]() 型台灯数量的
型台灯数量的![]() 倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?
倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,对角线互相垂直的四边形叫做垂美四边形.
(1)概念理解:如图2,在四边形![]() 中,
中,![]() ,问四边形
,问四边形![]() 是垂美四边形吗?请说明理由;
是垂美四边形吗?请说明理由;
(2)性质探究:如图1,四边形![]() 的对角线
的对角线![]() 交于点
交于点![]() ,
,![]() .
.
试证明:![]() ;
;
(3)解决问题:如图3,分别以![]() 的直角边
的直角边![]() 和斜边
和斜边![]() 为边向外作正方形
为边向外作正方形![]() 和正方形
和正方形![]() ,连结
,连结![]() .已知
.已知![]() ,求
,求![]() 的长.
的长.
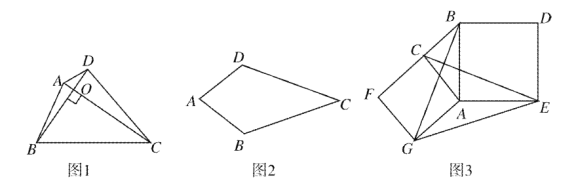
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着生活节奏的加快以及智能手机的普及,外卖点餐逐渐成为越来越多用户的餐饮消费习惯.由此催生了一批外卖点餐平台,已知某外卖平台的送餐费用与送餐距离有关(该平台只给5千米范围内配送),为调査送餐员的送餐收入,现从该平台随机抽取80名点外卖的用户进行统计,按送餐距离分类统计结果如下表:
送餐距离x(千米) | 0 | 1 | 2 | 3 | 4 |
数量 | 12 | 20 | 24 | 16 | 8 |
(1)从这80名点外卖的用户中任取一名用户,该用户的送餐距离不超过3千米的概率为 ;
(2)以这80名用户送餐距离为样本,同一组数据取该小组数据的中间值(例如第二小组(1<x ≤2)的中间值是1.5),试估计利用该平台点外卖用户的平均送餐距离;
(3)若该外卖平台给送餐员的送餐费用与送餐距离有关,不超过2千米时,每份3元;超过2千米但不超4千米时,每份5元;超过4千米时,每份9元. 以给这80名用户所需送餐费用的平均数为依据,若送餐员一天的目标收入不低于150元,试估计一天至少要送多少份外卖?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AB=10,BC=6,点O在射线![]() 上(点
上(点![]() 不与点
不与点![]() 重合),过点
重合),过点![]() 作
作![]() ,垂足为
,垂足为![]() ,以点
,以点![]() 为圆心,
为圆心,![]() 为半径画半圆
为半径画半圆![]() ,分别交射线
,分别交射线![]() 于
于![]() 、
、![]() 两点,设
两点,设![]() .
.
(1)如图,当点![]() 为
为![]() 边的中点时,求
边的中点时,求![]() 的值;
的值;
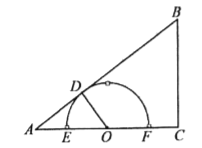
(2)如图,当点![]() 与点
与点![]() 重合时,连接
重合时,连接![]() ,求弦
,求弦![]() 的长;
的长;
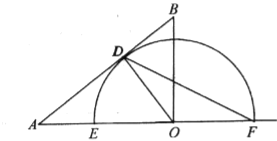
(3)当半圆![]() 与
与![]() 无交点时,直接写出
无交点时,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:
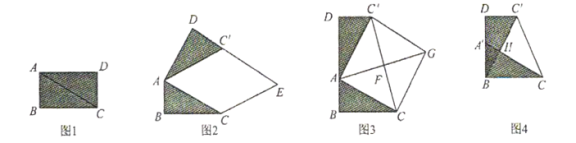
在综合与实践课上,老师让同学们以“矩形纸片的剪拼”为主题开展数学活动.如图1,将矩形纸片![]() 沿对角线
沿对角线![]() 剪开,得到
剪开,得到![]() 和
和![]() .并且量得
.并且量得![]() ,
,![]() .
.
操作发现:
(1)将图1中的![]() 以点
以点![]() 为旋转中心,按逆时针方向旋转
为旋转中心,按逆时针方向旋转![]() ,使
,使![]() ,得到如图2所示的
,得到如图2所示的![]() ,过点
,过点![]() 作
作![]() 的平行线,与
的平行线,与![]() 的延长线交于点
的延长线交于点![]() ,则四边形
,则四边形![]() 的形状是________.
的形状是________.
(2)创新小组将图1中的![]() 以点
以点![]() 为旋转中心,按逆时针方向旋转,使
为旋转中心,按逆时针方向旋转,使![]() 、
、![]() 、
、![]() 三点在同一条直线上,得到如图3所示的
三点在同一条直线上,得到如图3所示的![]() ,连接
,连接![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() 并延长至点
并延长至点![]() ,使
,使![]() ,连接
,连接![]() 、
、![]() ,得到四边形
,得到四边形![]() ,发现它是正方形,请你证明这个结论.
,发现它是正方形,请你证明这个结论.
实践探究:
(3)缜密小组在创新小组发现结论的基础上,进行如下操作:将![]() 沿着
沿着![]() 方向平移,使点
方向平移,使点![]() 与点
与点![]() 重合,此时
重合,此时![]() 点平移至
点平移至![]() 点,
点,![]() 与
与![]() 相交于点
相交于点![]() ,如图4所示,连接
,如图4所示,连接![]() ,试求
,试求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】陈先生驾车从杭州到上海,要经过一段高速公路,假设汽车在高速公路上匀速行驶,记行驶时间为t小时,速度为v千米/小时,如果陈先生驾车速度为90千米/小时,2小时可以通过高速公路.
(1)求v与t的函数表达式.
(2)高速公路的速度限定为不超过120千米/小时,陈先生计划10:00驶入高速,11:48前驾驶离开高速公路,求它的驾车速度v的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
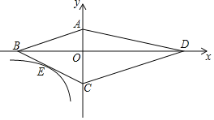
【题目】如图,四边形ABCD的顶点都在坐标轴上,若AB∥CD,![]() AOB与
AOB与![]() COD面积分别为8和18,若双曲线y=
COD面积分别为8和18,若双曲线y=![]() 恰好经过BC的中点E,则k的值为_____.
恰好经过BC的中点E,则k的值为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com