
【题目】如图,在Rt△ABC中,∠ACB=90°,AB=10,BC=6,点O在射线![]() 上(点
上(点![]() 不与点
不与点![]() 重合),过点
重合),过点![]() 作
作![]() ,垂足为
,垂足为![]() ,以点
,以点![]() 为圆心,
为圆心,![]() 为半径画半圆
为半径画半圆![]() ,分别交射线
,分别交射线![]() 于
于![]() 、
、![]() 两点,设
两点,设![]() .
.
(1)如图,当点![]() 为
为![]() 边的中点时,求
边的中点时,求![]() 的值;
的值;
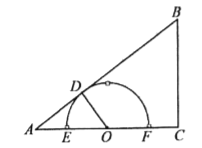
(2)如图,当点![]() 与点
与点![]() 重合时,连接
重合时,连接![]() ,求弦
,求弦![]() 的长;
的长;
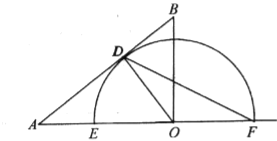
(3)当半圆![]() 与
与![]() 无交点时,直接写出
无交点时,直接写出![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)0<x<3或x>12
;(3)0<x<3或x>12
【解析】
(1)首先由勾股定理求出AC的长,再证明△AOD∽△ABC,得![]() ,代入相关数据从而可求出OD;
,代入相关数据从而可求出OD;
(2)首先根据等积法求出OD,再过点D作DH⊥AC,证明△DOH∽△ABO,求出DH、OH,最后在直角三角形DFH中运用勾股定理求出DF的长即可;
(3)分点O在点C左侧和点C右侧两种情况,运用相似三角形的性质求解即可.
(1)在Rt△ABC中,∵AB=10,BC=6,
∴![]() ,
,
∵点O为AC边的中点,
∴![]() .
.
∵OD⊥AB,∠ACB=90°,
∴∠ADO=∠ACB,
又∵∠A=∠A,
∴△AOD∽△ABC.
∴![]() ,即
,即![]() ,∴
,∴![]() .
.
(2) ∵点O与点C重合,OD⊥AB,
∴![]() OD·AB=
OD·AB=![]() AC·BC,即10x=8×6,
AC·BC,即10x=8×6,
∴![]() . 即OD=
. 即OD=![]()
过点D作DH⊥AC,垂足为H,则有∠DHO=∠ACB=90°.

∵∠DOH+∠BOD=90°,∠ABO+∠BOD=90°,
∴∠DOH=∠ABO,
∴△DOH∽△ABO,
∴![]() ,即
,即 ,
,
∴![]() ,
,![]() .
.
∵OF=OD=![]() ,
,
∴FH=OH+OF=![]() .
.
∴在Rt△DFH中,根据勾股定理,得:
∴![]() .
.
(3)①当点O在点C左侧,且与BC相切时,如图,

设OD=x,则OC=x,
∴AO=8-x,
∵∠ADO=∠ACB,∠A=∠A,
∴△AOD∽△ABC,
∴![]() ,
,
∵AB=10,BC=6,AO=8-x,
∴![]() ,解得,x=3,
,解得,x=3,
∴当半圆O在BC的左侧,且与BC无交点时,x的取值范围为:0<x<3;
②当点O在点C右侧,且与BC相切时,如图,
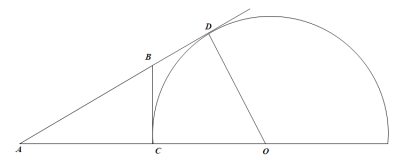
方法同①,得x=12,
∴当半圆O在BC的右侧,且与BC无交点时,x的取值范围为: x>12;
综上,当半圆![]() 与
与![]() 无交点时,x的取值范围是0<x<3或x>12.
无交点时,x的取值范围是0<x<3或x>12.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:
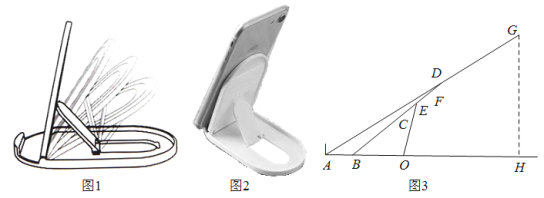
【题目】图1是一种手机托架,使用该手机托架示意图如图3所示,底部放置手机处宽![]() 厘米,托架斜面长
厘米,托架斜面长![]() 厘米,它有
厘米,它有![]() 到
到![]() 共4个档位调节角度,相邻两个档位间的距离为0.8厘米,档位
共4个档位调节角度,相邻两个档位间的距离为0.8厘米,档位![]() 到
到![]() 的距离为2.4厘米.将某型号手机置于托架上(图2),手机屏幕长
的距离为2.4厘米.将某型号手机置于托架上(图2),手机屏幕长![]() 是15厘米,
是15厘米,![]() 是支点且
是支点且![]() 厘米(支架的厚度忽略不计).当支架调到
厘米(支架的厚度忽略不计).当支架调到![]() 档时,点
档时,点![]() 离水平面的距离
离水平面的距离![]() 为_______厘米;当支架从
为_______厘米;当支架从![]() 档调到
档调到![]() 档时,点
档时,点![]() 离水平面的距离下降了_________厘米.
离水平面的距离下降了_________厘米.
查看答案和解析>>
科目:初中数学 来源: 题型:
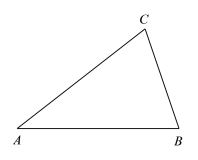
【题目】如图,已知△ABC中,AB=AC.
(1)把△ABC绕点C顺时针旋转得到△DEC,使得点B的对应点E落在AB边上,用尺规作图的方法作出△DEC;(保留作图痕迹,不写作法)
(2)在(1)的条件下,连接AD,求证:AD=BC.
查看答案和解析>>
科目:初中数学 来源: 题型:
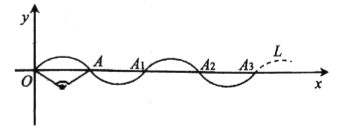
【题目】曲线![]() 在直角坐标系中的位置如图所示,曲线
在直角坐标系中的位置如图所示,曲线![]() 是由半径为2,圆心角为
是由半径为2,圆心角为![]() 的
的![]() (
(![]() 是坐标原点,点
是坐标原点,点![]() 在
在![]() 轴上)绕点
轴上)绕点![]() 旋转
旋转![]() ,得到
,得到![]() ;再将
;再将![]() 绕点
绕点![]() 旋转
旋转![]() ,得到
,得到![]() ;……依次类推,形成曲线
;……依次类推,形成曲线![]() ,现有一点
,现有一点![]() 从
从![]() 点出发,以每秒
点出发,以每秒![]() 个单位长度的速度,沿曲线
个单位长度的速度,沿曲线![]() 向右运动,则点
向右运动,则点![]() 的坐标为___________;在第
的坐标为___________;在第![]() 时,点
时,点![]() 的坐标为____________.
的坐标为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为鼓励学生阅读,某校开展了网上阅读室活动,校教务处为了解学生的阅读情况,随机抽查了部分学生最近一周参加网上阅读室的天数,并用得到的数据绘制了如下两幅统计图.
请根据图中提供的信息,回答下列问题:
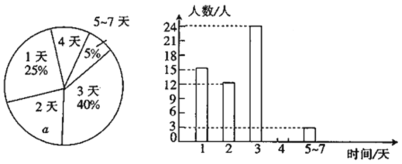
(1)![]() __________(百分比),本次调查的参加网上阅读室的天数的中位数为________.
__________(百分比),本次调查的参加网上阅读室的天数的中位数为________.
(2)请补全条形统计图.
(3)如果该校有3000名学生,请估算全校有多少名学生参加网上阅读室的天数不少于4天.
(4)在某班被调查的学生中,参加网上阅读室的天数不少于4天的有2名女同学,3名男同学.现要从中随机抽取2名同学代表班级参加阅读心得分享会,请用列表法或画树状图法求所抽取的2名同学恰好是一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着经济快速发展,环境问题越来越受到人们的关注.某校为了了解节能减排、垃圾分类等知识的普及情况,随机调查了部分学生,调查结果分为“非常了解”“了解”“了解较少”“不了解”四类,并将结果绘制成以下两幅不完整的统计图,请根据统计图回答下列问题:
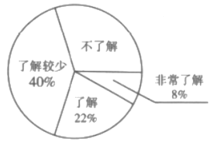
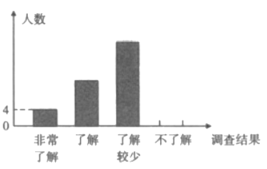
(1)本次调查的学生共有___________人,估计该校![]() 名学生中“不了解”的人数是__________人;
名学生中“不了解”的人数是__________人;
(2)将条形统计图补充完整;
(3)“非常了解”的![]() 人中有
人中有![]() ,
,![]() 两名男生,
两名男生,![]() ,
,![]() 两名女生,若从中随机抽取两人去参加环保知识竞赛,请用画树状图或列表的方法,求恰好抽到
两名女生,若从中随机抽取两人去参加环保知识竞赛,请用画树状图或列表的方法,求恰好抽到![]() 名男生的概率.
名男生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个四位数,记千位数字与个位数字之和为![]() ,十位数字与百位数字之和为
,十位数字与百位数字之和为![]() ,如果
,如果![]() ,那么称这个四位数为“对称数”
,那么称这个四位数为“对称数”
![]() 最小的“对称数”为 ;四位数
最小的“对称数”为 ;四位数![]() 与
与![]() 之和为最大的“对称数”,则
之和为最大的“对称数”,则![]() 的值为 ;
的值为 ;
![]() 一个四位的“对称数”
一个四位的“对称数”![]() ,它的百位数字是千位数字
,它的百位数字是千位数字![]() 的
的![]() 倍,个位数字与十位数字之和为
倍,个位数字与十位数字之和为![]() ,且千位数字
,且千位数字![]() 使得不等式组
使得不等式组 恰有
恰有![]() 个整数解,求出所有满足条件的“对称数”
个整数解,求出所有满足条件的“对称数”![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com