
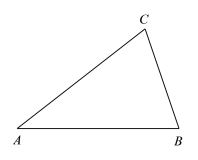
【题目】如图,已知△ABC中,AB=AC.
(1)把△ABC绕点C顺时针旋转得到△DEC,使得点B的对应点E落在AB边上,用尺规作图的方法作出△DEC;(保留作图痕迹,不写作法)
(2)在(1)的条件下,连接AD,求证:AD=BC.
【答案】(1)见解析;(2)见解析.
【解析】
(1)根据题目要求作图即可得;
(2)先证∠CEB=∠B,∠B=∠ACB得∠CEB=∠DCE,据此知DC∥AB,结合DC=AC,AB=AC可得四边形ABCD为平行四边形,从而证得结论.
(1)如图,△DEC即为所作.
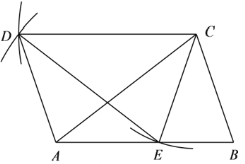
(2)∵△ABC绕点C顺时针旋转得到△DEC,
∴△ABC≌△DEC,DC=AC,EC=BC,
∵AB=AC,
∴DC=AB,
∵△ABC≌△DEC,
∴∠DCE=∠ACB,
∵EC=BC,
∴∠CEB=∠B,
∵AB=AC,
∴∠B=∠ACB,
∴∠CEB=∠DCE,
∴DC∥AB,
又∵DC=AC,AB=AC,
∴四边形ABCD是平行四边形,
∴AD=BC.


 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:
【题目】如图,在单位长度为1米的平面直角坐标系中,曲线是由半径为2米,圆心角为![]() 的
的![]() 多次复制并首尾连接而成.现有一点P从A(A为坐标原点)出发,以每秒
多次复制并首尾连接而成.现有一点P从A(A为坐标原点)出发,以每秒![]() 米的速度沿曲线向右运动,则在第2019秒时点P的纵坐标为( )
米的速度沿曲线向右运动,则在第2019秒时点P的纵坐标为( )
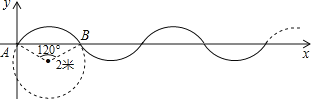
A. ﹣2B. ﹣1C. 0D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
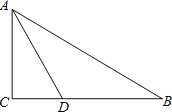
【题目】已知:如图,在![]() 中,
中,![]() 的角平分线
的角平分线![]() 交
交![]() 边于
边于![]() .
.
(1)以![]() 边上一点
边上一点![]() 为圆心,过
为圆心,过![]() 两点作
两点作![]() (不写作法,保留作图痕迹),再判断直线
(不写作法,保留作图痕迹),再判断直线![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)若(1)中的![]() 与
与![]() 边的另一个交点为
边的另一个交点为![]() ,
,![]() ,求线段
,求线段![]() 与劣弧
与劣弧![]() 所围成的图形面积.(结果保留根号和
所围成的图形面积.(结果保留根号和![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义:如图1,在![]() 中,把
中,把![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到
得到![]() ,把
,把![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,连接
,连接![]() .当
.当![]() 时,我们称
时,我们称![]() 是
是![]() 的“旋补三角形”,
的“旋补三角形”,![]() 边
边![]() 上的中线
上的中线![]() 叫做
叫做![]() 的“旋补中线”.
的“旋补中线”.
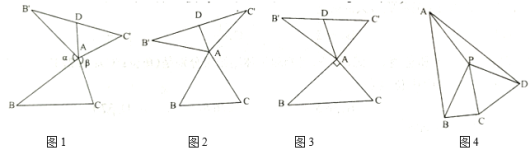
(特例感知)
(1)在图2,图3中,![]() 是
是![]() 的“旋补三角形”,
的“旋补三角形”,![]() 是
是![]() 的“旋补中线”.
的“旋补中线”.
①如图2,当![]() 为等边三角形,且
为等边三角形,且![]() 时,则
时,则![]() 长为 .
长为 .
②如图3,当![]() ,且
,且![]() 时,则
时,则![]() 长为 .
长为 .
(猜想论证)
(2)在图1中,当![]() 为任意三角形时,猜想
为任意三角形时,猜想![]() 与
与![]() 的数量关系,并给予证明.(如果你没有找到证明思路,可以考虑延长
的数量关系,并给予证明.(如果你没有找到证明思路,可以考虑延长![]() 或延长
或延长![]() ,……)
,……)
(拓展应用)
(3)如图4,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,以
,以![]() 为边在四边形
为边在四边形![]() 内部作等边
内部作等边![]() ,连接
,连接![]() ,
,![]() .若
.若![]() 是
是![]() 的“旋补三角形”,请直接写出
的“旋补三角形”,请直接写出![]() 的“旋补中线”长及四边形
的“旋补中线”长及四边形![]() 的边
的边![]() 长.
长.
查看答案和解析>>
科目:初中数学 来源: 题型:
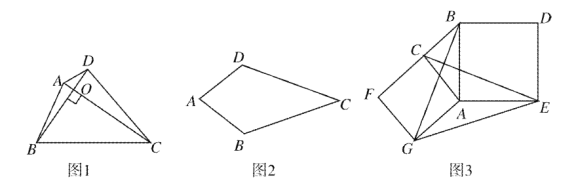
【题目】如图1,对角线互相垂直的四边形叫做垂美四边形.
(1)概念理解:如图2,在四边形![]() 中,
中,![]() ,问四边形
,问四边形![]() 是垂美四边形吗?请说明理由;
是垂美四边形吗?请说明理由;
(2)性质探究:如图1,四边形![]() 的对角线
的对角线![]() 交于点
交于点![]() ,
,![]() .
.
试证明:![]() ;
;
(3)解决问题:如图3,分别以![]() 的直角边
的直角边![]() 和斜边
和斜边![]() 为边向外作正方形
为边向外作正方形![]() 和正方形
和正方形![]() ,连结
,连结![]() .已知
.已知![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】连接正八边形的三个顶点,得到如图所示的图形,下列说法错误的是( )

A.四边形![]() 与四边形
与四边形![]() 的面积相等
的面积相等
B.连接![]() ,则
,则![]() 分别平分
分别平分![]() 和
和![]()
C.整个图形是轴对称图形,但不是中心对称图形
D.![]() 是等边三角形
是等边三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
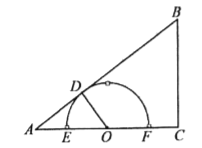
【题目】如图,在Rt△ABC中,∠ACB=90°,AB=10,BC=6,点O在射线![]() 上(点
上(点![]() 不与点
不与点![]() 重合),过点
重合),过点![]() 作
作![]() ,垂足为
,垂足为![]() ,以点
,以点![]() 为圆心,
为圆心,![]() 为半径画半圆
为半径画半圆![]() ,分别交射线
,分别交射线![]() 于
于![]() 、
、![]() 两点,设
两点,设![]() .
.
(1)如图,当点![]() 为
为![]() 边的中点时,求
边的中点时,求![]() 的值;
的值;
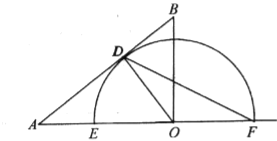
(2)如图,当点![]() 与点
与点![]() 重合时,连接
重合时,连接![]() ,求弦
,求弦![]() 的长;
的长;
(3)当半圆![]() 与
与![]() 无交点时,直接写出
无交点时,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小红将笔记本电脑水平放置在桌子上,当显示屏![]() 与底板
与底板![]() 所在水平线的夹角为120°时,感觉最舒适(如图1),侧面示意图如图2. 使用时为了散热,她在底板下垫入散热架
所在水平线的夹角为120°时,感觉最舒适(如图1),侧面示意图如图2. 使用时为了散热,她在底板下垫入散热架![]() 后,电脑转到
后,电脑转到![]() 位置(如图3),侧面示意图为图4. 已知
位置(如图3),侧面示意图为图4. 已知![]() ,
,![]() 于点
于点![]() ,
,![]() .
.
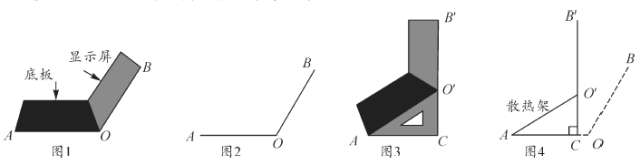
(1)求![]() 的度数.
的度数.
(2)显示屏的顶部![]() 比原来的顶部
比原来的顶部![]() 升高了多少?
升高了多少?
(3)如图4,垫入散热架后,要使显示屏![]() 与水平线的夹角仍保持120°,则显示屏
与水平线的夹角仍保持120°,则显示屏![]() 应绕点
应绕点![]() '按顺时针方向旋转多少度?并说明理由.
'按顺时针方向旋转多少度?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一溜娃神器推车,溜娃时该推车底部支架张开后,其框架投影图如图2所示,两支撑轮是分别以点![]() ,
,![]() 为圆心,1.5分米长为半径的圆且与水平地面相切,其支架长
为圆心,1.5分米长为半径的圆且与水平地面相切,其支架长![]() ,竖直支撑柱
,竖直支撑柱![]() 分米,水平座椅
分米,水平座椅![]() 分米,并与靠背
分米,并与靠背![]() 成
成![]() 夹角,推手柄
夹角,推手柄![]() 分米.当张开角
分米.当张开角![]() 时,
时,![]() ,
,![]() ,
,![]() 三点共线,且
三点共线,且![]() ,则
,则![]() 的长度为__________分米;如图3,当张开角
的长度为__________分米;如图3,当张开角![]() 时,折叠支撑柱以上座椅部分绕着点
时,折叠支撑柱以上座椅部分绕着点![]() 逆时针旋转使
逆时针旋转使![]() 点与圆心
点与圆心![]() 重合,此时手柄
重合,此时手柄![]() 绕着点
绕着点![]() 顺时针旋转
顺时针旋转![]() 至
至![]() 处,则
处,则![]() 到地面的距离是____________分米.
到地面的距离是____________分米.
图1 图2
图2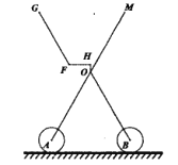 图3
图3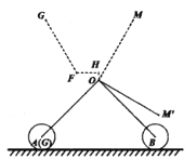
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com