
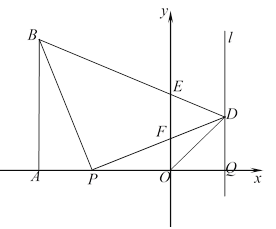
【题目】如图,在平面直角坐标系![]() 中,
中,![]()
![]() 轴于点
轴于点![]() .点
.点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度沿
个单位长度的速度沿![]() 轴向点
轴向点![]() 运动;点
运动;点![]() 从点
从点![]() 同时出发,以相同的速度沿
同时出发,以相同的速度沿![]() 轴的正方向运动,运动时间
轴的正方向运动,运动时间![]()
![]() .过点
.过点![]() 作平行于
作平行于![]() 轴的直线
轴的直线![]() ,连接
,连接![]() ,过
,过![]() 点作
点作![]() 交直线
交直线![]() 于点
于点![]() ,
,![]() 、
、![]() 与
与![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,连接
,连接![]() .
.
(1)当![]() 时,试求
时,试求![]() 的值;
的值;
(2)当![]() 为
为![]() 中点时,试求
中点时,试求![]() 的值;
的值;
(3)是否存在这样的![]() ,使得
,使得![]() 与
与![]() 的面积相等?若存在,求出所有符合条件的
的面积相等?若存在,求出所有符合条件的![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)当
;(3)当![]() 时,
时,![]() 与
与![]() 的面积相等
的面积相等
【解析】
(1))由题意知AP=OQ=t,先证明![]() ,得到DQ=AP,即∠DOQ=45,进而∠PDO=30,即可解答;
,得到DQ=AP,即∠DOQ=45,进而∠PDO=30,即可解答;
(2)过![]() 作
作![]() 于
于![]() ,由已知求出PO=OQ=DQ=2,进而得OD、PD长,再由等面积法求得OG,利用
,由已知求出PO=OQ=DQ=2,进而得OD、PD长,再由等面积法求得OG,利用![]() 即可求解;
即可求解;
(3)过![]() 作
作![]() ,交
,交![]() 于
于![]() ,交
,交![]() 轴于
轴于![]() ,由AB∥y轴得
,由AB∥y轴得![]() ,则有
,则有![]() ,进而求得EM、OE长,由
,进而求得EM、OE长,由![]() ,得
,得![]() ,即可得到OE=OP,代入得到关于t的方程,解之即可.(也可分别求出OE、OF、EF,由OE=OF+EF列方程求解)
,即可得到OE=OP,代入得到关于t的方程,解之即可.(也可分别求出OE、OF、EF,由OE=OF+EF列方程求解)
解:(1)![]() 轴
轴![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() 轴 ,
轴 ,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ;
;
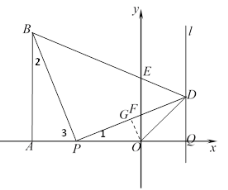
(2)过![]() 作
作![]() 于
于![]() .
.
![]() 为
为![]() 的中点
的中点![]()
![]() ,
,
在![]() 中,
中, ![]() ,
,
在![]() 中,
中, ![]() ,
,
![]()
![]() ,
,
![]() ,
,
(亦可通过![]() 求得)
求得)
∴在![]() 中,
中, ![]() ;
;
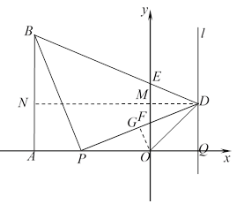
(3)过![]() 作
作![]() ,交
,交![]() 于
于![]() ,交
,交![]() 轴于
轴于![]() .
.
解法一:![]()
![]() ,
,
![]() ,
,
![]() ,
,
假设![]() ,则
,则![]() ,
,
![]() 即
即![]() ,
,
![]()
![]()
![]() ,
,
![]() (舍去),
(舍去),
因此,当![]() 时,
时,![]() 与
与![]() 的面积相等.
的面积相等.
解法二:![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() (舍去)
(舍去)
因此,当![]() 时,
时,![]() 与
与![]() 的面积相等.
的面积相等.


科目:初中数学 来源: 题型:
【题目】万州三中初中数学组深知人生最具好奇心和幻想力、创造力的时期是中学时代,经研究,为我校每一个初中生推荐一本中学生素质数育必读书《数学的奥秘》,这本书就是专门为好奇的中学生准备的.这本书不但给于我们知识,解答生活中的疑惑,更重要的是培养我们细致观察、认真思考、勤于动手的能力.经过一学期的阅读和学习,为了了解学生阅读效果,我们从初一、初二的学生中随机各选20名,对《数学的奥秘》此书阅读效果做测试(此次测试满分:100分).通过测试,我们收集到20名学生得分的数据如下:
初一 | 96 | 100 | 89 | 95 | 62 | 75 | 93 | 86 | 86 | 93 |
95 | 95 | 88 | 94 | 95 | 68 | 92 | 80 | 78 | 90 | |
初二 | 100 | 98 | 96 | 95 | 94 | 92 | 92 | 92 | 92 | 92 |
86 | 84 | 83 | 82 | 78 | 78 | 74 | 64 | 60 | 92 |
通过整理,两组数据的平均数、中位数、众数和方差如表:
年级 | 平均数 | 中位数 | 众数 | 方差 |
初一 | 87.5 | 91 | m | 96.15 |
初二 | 86.2 | n | 92 | 113.06 |
某同学将初一学生得分按分数段(![]() ,
,![]() ,
,![]() ,
,![]() ),绘制成频数分布直方图,初二同学得分绘制成扇形统计图,如图(均不完整),初一学生得分频数分布直方图 初二学生得分扇形统计图(注:x表示学生分数)
),绘制成频数分布直方图,初二同学得分绘制成扇形统计图,如图(均不完整),初一学生得分频数分布直方图 初二学生得分扇形统计图(注:x表示学生分数)
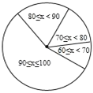
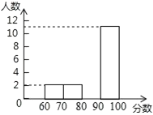
请完成下列问题:
(1)初一学生得分的众数![]() ________;初二学生得分的中位数
________;初二学生得分的中位数![]() ________;
________;
(2)补全频数分布直方图;扇形统计图中,![]() 所对用的圆心角为________度;
所对用的圆心角为________度;
(3)经过分析________学生得分相对稳定(填“初一”或“初二”);
(4)你认为哪个年级阅读效果更好,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,AB//DC,∠A=60°,AD=DC=BC=4,点E沿A→D→C→B运动,同时点F沿A→B→C运动,运动速度均为每秒1个单位,当两点相遇时,运动停止.则△AEF的面积y与运动时间x秒之间的图象大致为( )
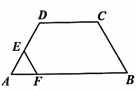
A. B.
B. C.
C.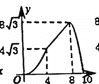 D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
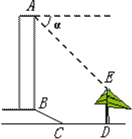
【题目】如图所示,某校教学楼正前方有一棵大树DE,高度是10米,从教学楼顶端A测得大树顶端E的俯角α是45°,大树低端D到教学楼前台阶底边的水平距离CD是15米,台阶坡长BC是6米,台阶的坡度i=1:![]() ,求教学楼AB的高度约为多少米?(结果精确到0.1米,参考数据:
,求教学楼AB的高度约为多少米?(结果精确到0.1米,参考数据:![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网店准备销售一种多功能旅行背包,计划从厂家以每个120元的价格进货.

(1)经过市场调查发现,当每个背包的售价为140元时,月均销量为980个,售价每增长10元,月均销量就相应减少30个,若使这种背包的月均销量不低于800个,每个背包售价应不高于多少元?
(2)在实际销售过程中,由于原材料涨价和生产成本增加的原因,每个背包的进价为150元,而每个背包的售价比(1)中最高售价减少了a%(a>0),月均销量比(1)中最低月均销量800个增加了5a%,结果该店销售该背包的月均利润达到了40000元,求在实际销售过程中每个背包售价为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
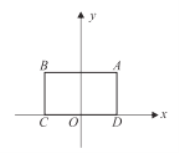
【题目】对于![]() 及一个矩形给出如下定义:如果
及一个矩形给出如下定义:如果![]() 上存在到此矩形四份顶点距离都相等的点,那么称
上存在到此矩形四份顶点距离都相等的点,那么称![]() 是该矩形的“等距圆”,如图,平面直角坐标系
是该矩形的“等距圆”,如图,平面直角坐标系![]() 中,矩形
中,矩形![]() 的顶点
的顶点![]() 坐标为
坐标为![]() ,顶点
,顶点![]() 在
在![]() 轴上,
轴上,![]() ,且
,且![]() 的半径为
的半径为![]() .
.
(1)在![]() ,
,![]() ,
,![]() 中可以成为矩形
中可以成为矩形![]() 的“等距圆”的圆心的是__________.
的“等距圆”的圆心的是__________.
(2)如果点![]() 在直线
在直线![]() 上,且
上,且![]() 是矩形的“等距圆”,那么点
是矩形的“等距圆”,那么点![]() 的坐标为__________.
的坐标为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某某用户培育了甲乙两种番茄,各随机抽取了10棵幼苗,测试高度如下(单位:cm)
甲:10,9,10,10,13,8,7,12,10,11
乙:9,10,8,11,10,11,10,9,10,12
你认为哪种番茄长得比较整齐?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司生产的一种产品按照质量由高到低分为A,B,C,D四级,为了增加产量、提高质量,该公司改进了一次生产工艺,使得生产总量增加了一倍.为了解新生产工艺的效果,对改进生产工艺前、后的四级产品的占比情况进行了统计,绘制了如下扇形图:
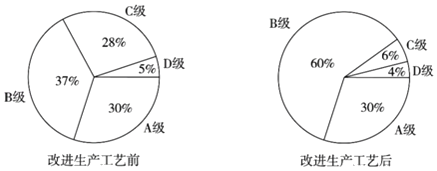
根据以上信息,下列推断合理的是( )
A.改进生产工艺后,A级产品的数量没有变化
B.改进生产工艺后,B级产品的数量增加了不到一倍
C.改进生产工艺后,C级产品的数量减少
D.改进生产工艺后,D级产品的数量减少
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com