
【题目】关于x的一元二次方程![]() 有实数根.
有实数根.
(1)求m的取值范围;
(2)当m为正整数时,取一个合适的值代入求出方程的解.
科目:初中数学 来源: 题型:
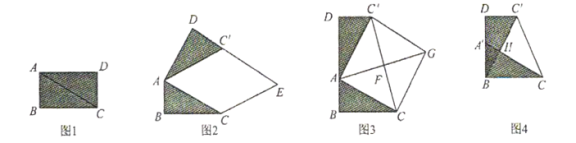
【题目】问题情境:
在综合与实践课上,老师让同学们以“矩形纸片的剪拼”为主题开展数学活动.如图1,将矩形纸片![]() 沿对角线
沿对角线![]() 剪开,得到
剪开,得到![]() 和
和![]() .并且量得
.并且量得![]() ,
,![]() .
.
操作发现:
(1)将图1中的![]() 以点
以点![]() 为旋转中心,按逆时针方向旋转
为旋转中心,按逆时针方向旋转![]() ,使
,使![]() ,得到如图2所示的
,得到如图2所示的![]() ,过点
,过点![]() 作
作![]() 的平行线,与
的平行线,与![]() 的延长线交于点
的延长线交于点![]() ,则四边形
,则四边形![]() 的形状是________.
的形状是________.
(2)创新小组将图1中的![]() 以点
以点![]() 为旋转中心,按逆时针方向旋转,使
为旋转中心,按逆时针方向旋转,使![]() 、
、![]() 、
、![]() 三点在同一条直线上,得到如图3所示的
三点在同一条直线上,得到如图3所示的![]() ,连接
,连接![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() 并延长至点
并延长至点![]() ,使
,使![]() ,连接
,连接![]() 、
、![]() ,得到四边形
,得到四边形![]() ,发现它是正方形,请你证明这个结论.
,发现它是正方形,请你证明这个结论.
实践探究:
(3)缜密小组在创新小组发现结论的基础上,进行如下操作:将![]() 沿着
沿着![]() 方向平移,使点
方向平移,使点![]() 与点
与点![]() 重合,此时
重合,此时![]() 点平移至
点平移至![]() 点,
点,![]() 与
与![]() 相交于点
相交于点![]() ,如图4所示,连接
,如图4所示,连接![]() ,试求
,试求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现
如图![]() , 在
, 在![]() 和
和![]() 中,
中,![]() ,
,![]() ,
,![]() , 连接
, 连接![]() ,
,![]() 交于点
交于点![]() .填空:①
.填空:①![]() 的值为 :②
的值为 :②![]() 的度数为
的度数为
(2)类比探究
如图![]() , 在
, 在![]() 和
和![]() 中,
中,![]() ,
,![]() , 连接
, 连接![]() 交
交![]() 的延长线于点
的延长线于点![]() .请求出
.请求出![]() 能的值及
能的值及![]() 的度数, 并说明理由;
的度数, 并说明理由;
(3)拓展延伸
在![]() 的条件下, 将
的条件下, 将![]() 绕点
绕点![]() 在平面内旋转,
在平面内旋转,![]() 所在直线交于点
所在直线交于点![]() , 若
, 若![]() ,
,![]() ,请直接写出当点
,请直接写出当点![]() 与点
与点![]() 重合时
重合时![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
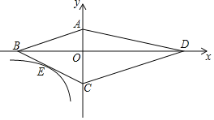
【题目】如图,四边形ABCD的顶点都在坐标轴上,若AB∥CD,![]() AOB与
AOB与![]() COD面积分别为8和18,若双曲线y=
COD面积分别为8和18,若双曲线y=![]() 恰好经过BC的中点E,则k的值为_____.
恰好经过BC的中点E,则k的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实行垃圾分类和垃圾资源化利用,关系广大人民群众生活环境,关系节约使用资源,也是社会文明水平的一个重要体现.某环保公司研发了甲、乙两种智能设备,可利用最新技术将干垃圾进行分选破碎制成固化成型燃料棒,干垃圾由此变身新型清洁燃料.某垃圾处理厂从环保公司购入以上两种智能设备若干,已知购买甲型智能设备花费![]() 万元,购买乙型智能设备花费
万元,购买乙型智能设备花费![]() 万元,购买的两种设备数量相同,且两种智能设备的单价和为
万元,购买的两种设备数量相同,且两种智能设备的单价和为![]() 万元.
万元.
![]() 求甲、乙两种智能设备单价;
求甲、乙两种智能设备单价;
![]() 垃圾处理厂利用智能设备生产燃料棒,并将产品出售.已知燃料棒的成本由人力成本和物资成本两部分组成,其中物资成本占总成本的
垃圾处理厂利用智能设备生产燃料棒,并将产品出售.已知燃料棒的成本由人力成本和物资成本两部分组成,其中物资成本占总成本的![]() ,且生产每吨燃料棒所需人力成本比物资成本的倍
,且生产每吨燃料棒所需人力成本比物资成本的倍![]() 还多
还多![]() 元.调查发现,若燃料棒售价为每吨
元.调查发现,若燃料棒售价为每吨![]() 元,平均每天可售出
元,平均每天可售出![]() 吨,而当销售价每降低
吨,而当销售价每降低![]() 元,平均每天可多售出
元,平均每天可多售出![]() 吨.垃圾处理厂想使这种燃料棒的销售利润平均每天达到
吨.垃圾处理厂想使这种燃料棒的销售利润平均每天达到![]() 元,且保证售价在每吨
元,且保证售价在每吨![]() 元基础上降价幅度不超过
元基础上降价幅度不超过![]() ,求每吨燃料棒售价应为多少元?
,求每吨燃料棒售价应为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
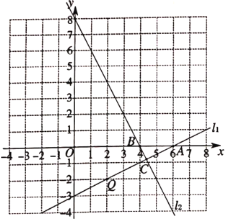
【题目】如图,直线![]() 经过点
经过点![]() ,与x轴交于点
,与x轴交于点![]() ,直线
,直线![]() 与x轴相交于点B,与直线
与x轴相交于点B,与直线![]() 相交于点C.
相交于点C.
(1)求直线![]() 的表达式;
的表达式;
(2)M的坐标为![]() ,当
,当![]() 取最小时.
取最小时.
①求M点坐标;
②横,纵坐标都是整数的点叫做整点.直接写出线段AM、BM、BC、AC围成区域内(不包括边界)整点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是等边三角形ABC内一点,且PA=3,PB=4, PC=5,若将△APB绕着点B逆时针旋转后得到△CQB,则∠APB的度数______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形纸片ABCD中,已知AD =8,折叠纸片使AB边与对角线AC
重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为( )

A. 3 B. 4
C. 5 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(1,0)和点B,与y轴的正半轴交于点C.现有下列结论:①abc>0;②4a﹣2b+c>0;③2a﹣b>0;④3a+c=0,其中,正确结论的个数是( )
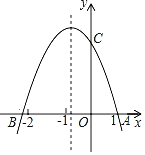
A.1B.2C.3D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com