
科目: 来源: 题型:
【题目】《九章算术》是我国古代数学的经典著作,书中有一个问题:“今有黄金九枚,白银一十一枚,称之重适等,交易其一,金轻十三两,问金、银各重几何?”意思是:甲袋中装有黄金9枚(每枚黄金重量相同),乙袋中装有白银11枚(每枚白银重量相同),称重两袋相等,两袋互相交换1枚后,甲袋比乙袋轻了13两(袋子重量忽略不计),问黄金、白银每枚各重多少两?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(﹣1,0),与y轴的交点为C,已知﹣2≤c≤﹣1,顶点坐标为(1,n),则下列结论正确的是( )

A.a+b>0
B.![]()
C.对于任意实数m,不等式a+b>am2+bm恒成立
D.关于x的方程ax2+bx+c=n+1没有实数根
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,点![]() 在抛物线上,将抛物线
在抛物线上,将抛物线![]() 在点
在点![]() 右侧的部分沿着直线
右侧的部分沿着直线![]() 翻折,翻折后的图象与原抛物线剩余部分合称为图象
翻折,翻折后的图象与原抛物线剩余部分合称为图象![]() .
.
(1)当![]() 时,
时,
①在如图的平面直角坐标系中画出图象![]() ;
;
②直接写出图象![]() 对应函数的表达式;
对应函数的表达式;
③当![]() 时,图象
时,图象![]() 对应函数的最小值为
对应函数的最小值为![]() 求
求![]() 的取值范围.
的取值范围.
(2)当![]() 时,直接写出图象
时,直接写出图象![]() 对应函数
对应函数![]() 随
随![]() 增大而减小时
增大而减小时![]() 的取值范围.
的取值范围.
(3)若图象![]() 上有且只有三个点到直线
上有且只有三个点到直线![]() 的距离为
的距离为![]() ,直接写出
,直接写出![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在![]() 中,
中,![]() 为边
为边![]() 的中点.点
的中点.点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度沿
个单位长度的速度沿![]() 运动到点
运动到点![]() 停止,同时点
停止,同时点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度沿折线
个单位长度的速度沿折线![]() 运动到点
运动到点![]() 停止,当点
停止,当点![]() 停止运动时,点
停止运动时,点![]() 也停止运动.当点
也停止运动.当点![]() 不与
不与![]() 的顶点重合时,过点
的顶点重合时,过点![]() 作
作![]() 交
交![]() 的边于点
的边于点![]() 以
以![]() 和
和![]() 为边作
为边作![]() ,设点
,设点![]() 的运动时间为
的运动时间为![]() (秒),
(秒),![]() 的面积为
的面积为![]() (平方单位).
(平方单位).
(1)当点![]() 与点
与点![]() 重合时,求
重合时,求![]() 的值;
的值;
(2)用含![]() 的代数式表示
的代数式表示![]() 的长;
的长;
(3)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(4)连结![]() 直接写出
直接写出![]() 将
将![]() 分成面积相等的两部分时
分成面积相等的两部分时![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】数学兴趣活动课上,小致将等腰![]() 的底边
的底边![]() 与直线
与直线![]() 重合.
重合.
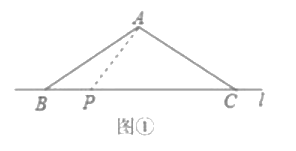
(1)如图![]() ,在
,在![]() 中,
中,![]() ,点
,点![]() 在边
在边![]() 所在的直线
所在的直线![]() 上移动,根据“直线外一点到直线上所有点的连线中垂线段最短”,小致发现
上移动,根据“直线外一点到直线上所有点的连线中垂线段最短”,小致发现![]() 的最小值是____________.
的最小值是____________.
(2)为进一步运用该结论,在(1)的条件下,小致发现,当![]() 最短时,如图
最短时,如图![]() ,在
,在![]() 中,作
中,作![]() 平分
平分![]() 交
交![]() 于点
于点![]() 点
点![]() 分别是边
分别是边![]() 上的动点,连结
上的动点,连结![]() 小致尝试探索
小致尝试探索![]() 的最小值,小致在
的最小值,小致在![]() 上截取
上截取![]() 使得
使得![]() 连结
连结![]() 易证
易证![]() ,从而将
,从而将![]() 转化为
转化为![]() 转化到(1)的情况,则
转化到(1)的情况,则![]() 的最小值为 ;
的最小值为 ;
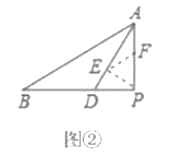
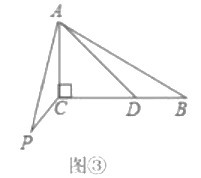
(3)解决问题:如图![]() ,在
,在![]() 中,
中,![]() ,点
,点![]() 是边
是边![]() 上的动点,连结
上的动点,连结![]() 将线段
将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,得到线段
,得到线段![]() 连结
连结![]() ,求线段
,求线段![]() 的最小值.
的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】根据市卫生防疫部门的要求,游泳池必须定期换水后才能对外开放.在换水时需要经“排水一清冼一灌水”的过程.某游泳馆从早上![]() 开始对游泳池进行换水,已知该游泳池的排水速度是灌水速度的
开始对游泳池进行换水,已知该游泳池的排水速度是灌水速度的![]() 倍,其中游泳池内剩余的水量
倍,其中游泳池内剩余的水量![]() 与换水时间上
与换水时间上![]() 之间的函数图象如图所示,根据图象解答下列问题:
之间的函数图象如图所示,根据图象解答下列问题:
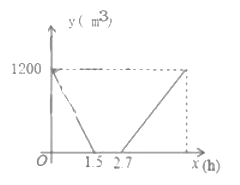
(1)该游泳池清洗需要 小时.
(2)求排水过程中的![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围.
的取值范围.
(3)若该游泳馆在换水结束![]() 分钟后才能对外开放,判断游泳爱好者小致能否在中午
分钟后才能对外开放,判断游泳爱好者小致能否在中午![]() 进入该游泳馆游泳,并说明理由.
进入该游泳馆游泳,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】图![]() 、图
、图![]() 均是
均是![]() 的正方形网格,每个小正方形的顶点称为格点,
的正方形网格,每个小正方形的顶点称为格点,![]() 的顶点均在格点上,点
的顶点均在格点上,点![]() 为边
为边![]() 的中点.分别在图
的中点.分别在图![]() 、图
、图![]() 中
中![]() 的边
的边![]() 上确定点
上确定点![]() 并作出直线
并作出直线![]() ,使
,使![]() 与
与![]() 相似.
相似.
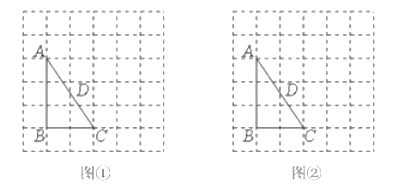
要求:(1)图![]() 、图
、图![]() 中的点
中的点![]() 位置不同.
位置不同.
(2)只用无刻度的直尺,保留适当的作图痕迹.
查看答案和解析>>
科目: 来源: 题型:
【题目】伊利集团是中国规模最大、产品线最全的乳制品企业.综合实践小组的同学从网上搜集到如下一些伊利集团近几年的营业状况的资料,其中图1是2013-2018年伊利集团营业收入及净利润情况统计图,图2是2018年伊利集团各品类业务营业、收入比例情况统计图(数据来源:公司财报、中商产业研究院).
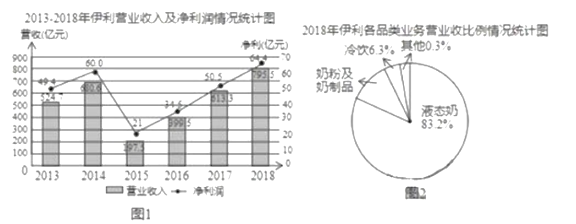
综合实践小组的同学结合统计图提出了如下问题,请你解答:
(1)2018年,伊利集团营收及净利再次刷新行业记录,稳居亚洲乳业第一,这一年,伊利集团实现营业收入 亿元,净利润 亿元.
(2)求2018年伊利集团“奶粉及奶制品”业务的营业收入(结果精确到![]() 亿元).
亿元).
(3)在2013-2018这![]() 年中,伊利集团的净利比上一年增长额最多的是 年;估计2019年伊利集团的净利润将比上一年增长 亿元,并说明理由.
年中,伊利集团的净利比上一年增长额最多的是 年;估计2019年伊利集团的净利润将比上一年增长 亿元,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
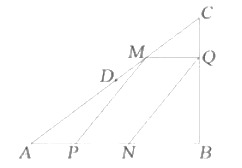
【题目】如图,平面直角坐标系中,四边形OABC为矩形,点A、B的坐标分别为(6,0),(6,8).动点M、N分别从O、B同时出发,以每秒1个单位的速度运动.其中,点M沿OA向终点A运动,点N沿BC向终点C运动.过点N作NP⊥BC,交AC于P,连接MP.已知动点运动了x秒.
(1)P点的坐标为多少;(用含x的代数式表示)
(2)试求△MPA面积的最大值,并求此时x的值;
(3)请你探索:当x为何值时,△MPA是一个等腰三角形?你发现了几种情况?写出你的研究成果.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com