
科目: 来源: 题型:
【题目】如图,AB是⊙O的直径,点C在AB的延长线上,AD平分∠CAE交⊙O于点D,且AE⊥CD,垂足为点E.
(1)求证:直线CE是⊙O的切线.
(2)若BC=3,CD=3![]() ,求弦AD的长.
,求弦AD的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】(本小题满分10分)
如图,在□ABCD中,以点A为圆心,AB长为半径画弧交AD于点F;再分别以点B、F为圆心,大于![]() BF的相同长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF,则所得四边形ABEF是菱形.
BF的相同长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF,则所得四边形ABEF是菱形.
(1)根据以上尺规作图的过程,求证四边形ABEF是菱形;
(2)若菱形ABEF的周长为16,AE=4![]() ,求∠C的大小.
,求∠C的大小.

查看答案和解析>>
科目: 来源: 题型:
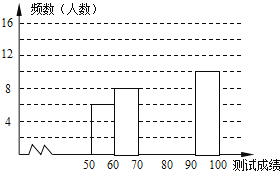
【题目】“赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
组别 | 成绩x分 | 频数 |
第1组 |
| 6 |
第2组 |
| 8 |
第3组 |
| 14 |
第4组 |
| a |
第5组 |
| 10 |
请结合图表完成下列各题:
![]() 求表中a的值;
求表中a的值; ![]() 频数分布直方图补充完整;
频数分布直方图补充完整;
![]() 若测试成绩不低于80分为优秀,则本次测试的优秀率是多少?
若测试成绩不低于80分为优秀,则本次测试的优秀率是多少?
![]() 第5组10名同学中,有4名男同学,现将这10名同学平均分成两组进行对抗练习,且4名男同学每组分两人,求小明与小强两名男同学能分在同一组的概率.
第5组10名同学中,有4名男同学,现将这10名同学平均分成两组进行对抗练习,且4名男同学每组分两人,求小明与小强两名男同学能分在同一组的概率.
查看答案和解析>>
科目: 来源: 题型:
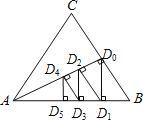
【题目】如图,△ABC是一个边长为2的等边三角形,AD0⊥BC,垂足为点D0.过点D0作D0D1⊥AB,垂足为点D1;再过点D1作D1D2⊥AD0,垂足为点D2;又过点D2作D2D3⊥AB,垂足为点D3;…;这样一直作下去,得到一组线段:D0D1,D1D2,D2D3,…,则线段Dn﹣1Dn的长为_____(n为正整数).
查看答案和解析>>
科目: 来源: 题型:
【题目】有两张完全重合的矩形纸片,小亮同学将其中一张绕点A顺时针旋转90°后得到矩形AMEF(如图1),连接BD、MF,若此时他测得BD=8cm,∠ADB=30度.请回答下列问题:(1)试探究线段BD与线段MF的关系,并简要说明理由;
(2)小红同学用剪刀将△BCD与△MEF剪去,与小亮同学继续探究.他们将△ABD绕点A顺时针旋转得△AB1D1,AD1交FM于点K(如图2),设旋转角为β(0°<β<90°),当△AFK为等腰三角形时,请直接写出旋转角β的度数;
(3)若将△AFM沿AB方向平移得到△A2F2M2(如图3),F2M2与AD交于点P,A2M2与BD交于点N,当NP∥AB时,求平移的距离是多少?

查看答案和解析>>
科目: 来源: 题型:
【题目】若抛物线L:y=ax2+bx+c(a,b,c是常数,abc≠0)与直线l都经过y轴上的同一点,且抛物线L的顶点在直线l上,则称次抛物线L与直线l具有“一带一路”关系,并且将直线l叫做抛物线L的“路线”,抛物线L叫做直线l的“带线”.
(1)若“路线”l的表达式为y=2x﹣4,它的“带线”L的顶点的横坐标为﹣1,求“带线”L的表达式;
(2)如果抛物线y=mx2﹣2mx+m﹣1与直线y=nx+1具有“一带一路”关系,求m,n的值;
(3)设(2)中的“带线”L与它的“路线”l在y轴上的交点为A.已知点P为“带线”L上的点,当以点P为圆心的圆与“路线”l相切于点A时,求出点P的坐标.
查看答案和解析>>
科目: 来源: 题型:
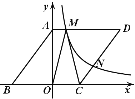
【题目】如图,菱形ABCD的顶点A在y轴正半轴上,边BC在x轴上,且BC=5,sin∠ABC=![]() ,反比例函数
,反比例函数![]() (x>0)的图象分别与AD,CD交于点M、点N,点N的坐标是(3,n),连接OM,MC.
(x>0)的图象分别与AD,CD交于点M、点N,点N的坐标是(3,n),连接OM,MC.
(1)求反比例函数的解析式;
(2)求证:△OMC是等腰三角形.
查看答案和解析>>
科目: 来源: 题型:
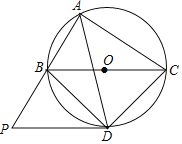
【题目】如图,⊙O是△ABC的外接圆,O点在BC边上,∠BAC的平分线交⊙O于点D,连接BD、CD,过点D作BC的平行线,与AB的延长线相交于点P.
(1)求证:PD是⊙O的切线;
(2)若AB=3,AC=4,求线段PB的长.
查看答案和解析>>
科目: 来源: 题型:
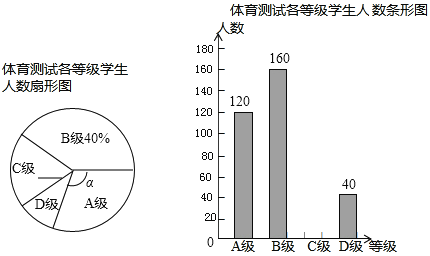
【题目】2018年某市学业水平体育测试即将举行,某校为了解同学们的训练情况,从九年级学生中随机抽取部分学生进行了体育测试(把成绩分为四个等级:A级:优秀;B级:良好;C级:及格;D级:不及格),并将测试结果绘成了如下两幅不完整的统计图,请根据统计图中的信息解答下列问题:
(1)求本次抽测的学生人数;
(2)求扇形图中∠α的度数,并把条形统计图补充完整;
(3)在测试中甲乙、丙、丁四名同学表现非常优秀,现决定从这四名同学中任选两名给大家介绍训练经验,求恰好选中甲、乙两名同学的概率(用树状图或列表法解答).
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,正方形OA1B1C1的边长为1,以O为圆心,OA1为半径作扇形OA1C1,弧A1C1与OB1相交于点B2,设正方形OA1B1C1与扇形OA1C1之间的阴影部分的面积为S1;然后以OB2为对角线作正方形OA2B2C2,又以O为圆心,OA2为半径作扇形OA2C2,弧A2C2与OB1相交于点B3,设正方形OA2B2C2与扇形OA2C2之间的阴影部分面积为S2;按此规律继续作下去,设正方形OA2018B2018C2018与扇形OA2018C2018之间的阴影部分面积为S2018,则S2018=____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com