
科目: 来源: 题型:
【题目】如图,从地面上的点A看一山坡上的电线杆PQ,测得杆顶端点P的仰角是45°,向前走6m到达B点,测得杆顶端点P和杆底端点Q的仰角分别是60°和30°.
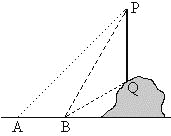
(1)求∠BPQ的度数;
(2)求该电线杆PQ的高度(结果精确到1m).备用数据:![]() ,
,![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】从甲、乙两位运动员中选出一名参加在规定时间内的投篮比赛.预先对这两名运动员进行了6次测试,成绩如下(单位:个):
甲:6,12,8,12,10,12;
乙:9,10,11,10,12,8;
(1)填表:
平均数 | 众数 | 方差 | |
甲 | 10 |
|
|
乙 |
| 10 |
|
(2)根据测试成绩,请你运用所学的统计知识作出分析,派哪一位运动员参赛更好?为什么?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,边长为2的正方形ABCD的顶点A、B在一个半径为2的圆上,顶点C、D在圆内,将正方形ABCD沿圆的内壁作无滑动的滚动.当滚动一周回到原位置时,点C运动的路径长为_____.
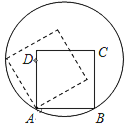
查看答案和解析>>
科目: 来源: 题型:
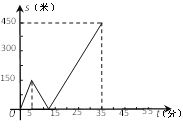
【题目】甲乙两人匀速从同一地点到1500米处的图书馆看书,甲出发5分钟后,乙以50米/分的速度沿同一路线行走.设甲乙两人相距![]() (米),甲行走的时间为
(米),甲行走的时间为![]() (分),
(分),![]() 关于
关于![]() 的函数函数图像的一部分如图所示.
的函数函数图像的一部分如图所示.
(1)求甲行走的速度;
(2)在坐标系中,补画![]() 关于
关于![]() 函数图象的其余部分;
函数图象的其余部分;
(3)问甲、乙两人何时相距360米?
查看答案和解析>>
科目: 来源: 题型:
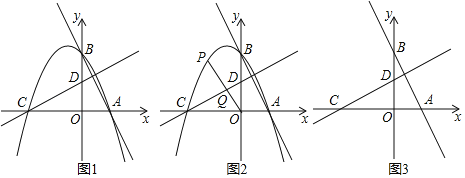
【题目】如图1,在平面直角坐标系中,直线AB:y=kx+b(k<0,b>0),与x轴交于点A、与y轴交于点B,直线CD与x轴交于点C、与y轴交于点D.若直线CD的解析式为y=﹣![]() (x+b),则称直线CD为直线AB的”姊线”,经过点A、B、C的抛物线称为直线AB的“母线”.
(x+b),则称直线CD为直线AB的”姊线”,经过点A、B、C的抛物线称为直线AB的“母线”.
(1)若直线AB的解析式为:y=﹣3x+6,求AB的”姊线”CD的解析式为: (直接填空);
(2)若直线AB的”母线”解析式为:![]() ,求AB的”姊线”CD的解析式;
,求AB的”姊线”CD的解析式;
(3)如图2,在(2)的条件下,点P为第二象限”母线”上的动点,连接OP,交”姊线”CD于点Q,设点P的横坐标为m,PQ与OQ的比值为y,求y与m的函数关系式,并求y的最大值;
(4)如图3,若AB的解析式为:y=mx+3(m<0),AB的“姊线”为CD,点G为AB的中点,点H为CD的中点,连接OH,若GH=![]() ,请直接写出AB的”母线”的函数解析式.
,请直接写出AB的”母线”的函数解析式.
查看答案和解析>>
科目: 来源: 题型:
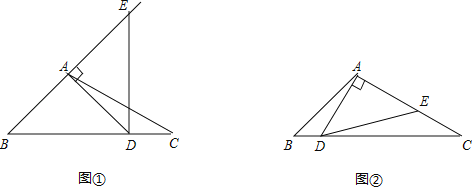
【题目】在△ABC中,∠B=45°,∠C=30°,点D是边BC上一点,连接AD,将线段AD绕点A逆时针旋转90°,得到线段AE,连接DE.
(1)如图①,当点E落在边BA的延长线上时,∠EDC= 度(直接填空);
(2)如图②,当点E落在边AC上时,求证:BD=![]() EC;
EC;
(3)当AB=2![]() ,且点E到AC的距离等于
,且点E到AC的距离等于![]() ﹣1时,直接写出tan∠CAE的值.
﹣1时,直接写出tan∠CAE的值.
查看答案和解析>>
科目: 来源: 题型:
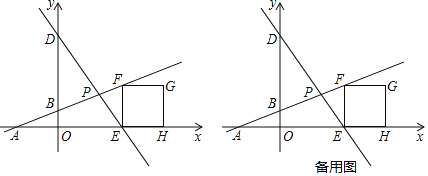
【题目】如图,在平面直角坐标系中,直线DE交x轴于点E(30,0),交y轴于点D(0,40),直线AB:y=![]() x+5交x轴于点A,交y轴于点B,交直线DE于点P,过点E作EF⊥x轴交直线AB于点F,以EF为一边向右作正方形EFGH.
x+5交x轴于点A,交y轴于点B,交直线DE于点P,过点E作EF⊥x轴交直线AB于点F,以EF为一边向右作正方形EFGH.
(1)求边EF的长;
(2)将正方形EFGH沿射线FB的方向以每秒![]() 个单位的速度匀速平移,得到正方形E1F1G1H1,在平移过程中边F1G1始终与y轴垂直,设平移的时间为t秒(t>0).
个单位的速度匀速平移,得到正方形E1F1G1H1,在平移过程中边F1G1始终与y轴垂直,设平移的时间为t秒(t>0).
①当点F1移动到点B时,求t的值;
②当G1,H1两点中有一点移动到直线DE上时,请直接写出此时正方形E1F1G1H1与△APE重叠部分的面积.
查看答案和解析>>
科目: 来源: 题型:
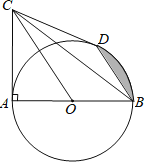
【题目】如图,AB为⊙O的直径,C为⊙O外一点,且∠CAB=90°,BD是⊙O的弦,BD∥CO.
(1)请说明:CD是⊙O的切线:
(2)若AB=4,BC=2![]() .则阴影部分的面积为
.则阴影部分的面积为
查看答案和解析>>
科目: 来源: 题型:
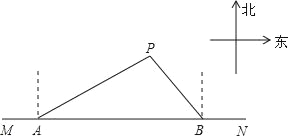
【题目】如图,在东西方向的海岸线MN上有A、B两艘船,均收到已触礁搁浅的船P的求救信号,已知船P在船A的北偏东58°方向,船P在船B的北偏西35°方向,AP的距离为30海里(参考数据:sin32°≈0.53,sin55°≈0.82).
(1)求船P到海岸线MN的距离(精确到0.1海里);
(2)若船A、船B分别以20海里/小时、15海里/小时的速度同时出发,匀速直线前往救援,试通过计算判断哪艘船先到达船P处.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com