
【题目】如图,AB为⊙O的直径,C为⊙O外一点,且∠CAB=90°,BD是⊙O的弦,BD∥CO.
(1)请说明:CD是⊙O的切线:
(2)若AB=4,BC=2![]() .则阴影部分的面积为
.则阴影部分的面积为
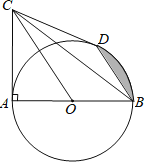
【答案】(1)详见解析;(2)![]()
【解析】
(1)连接OD,易证△CAO≌△CDO(SAS),由全等三角形的性质可得∠CDO=∠CAO=90°,即CD⊥OD,进而可证明CD是⊙O的切线;
(2)过点O作OE⊥BD,垂足为E,首先利用勾股定理可求出AC,OC的长,证得△OBD是等边三角形,根据扇形和三角形的面积公式即可得到结论.
(1)证明:如图,连接OD,
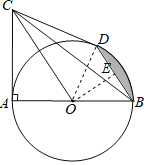
∵BD∥CO,
∴∠DBO=∠COA,∠ODB=∠COD,
在⊙O中,OB=OD,
∴∠DBO=∠ODB,
∴∠COA=∠COD,
在△CAO和△CDO中,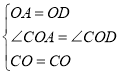 ,
,
∴△CAO≌△CDO(SAS).,
∴∠CDO=∠CAO=90°,
即 CD⊥OD,
又∵OD是⊙O的半径,
∴CD是⊙O的切线;
(2)如图,过点O作OE⊥BD,垂足为E.
在Rt△ABC中,AC=![]() ,
,
∴OC=![]() =4,
=4,
∴∠AOC=60°,
∵△CAO≌△CDO,
∴∠COD=∠COA=60°,
∴∠BOD=60°,
∴△BOD是等边三角形,
∴BD=OD=2,OE=![]() ,
,
∴阴影部分的面积=S扇形BOD﹣S△BOD=![]() ﹣
﹣![]() ×2×
×2×![]() =
=![]() π﹣
π﹣![]() .
.
故答案为:![]() π﹣
π﹣![]() .
.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
【题目】某中学为了丰富同学们的课外活动生活,开设了“第二课堂”.课堂设置了十几个动项目,根据(1)班学生报名参加的项目,绘制成如下的不完整的条形统计图和扇形统计图.
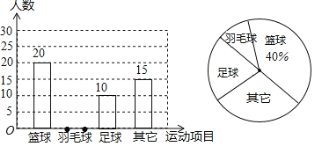
结合图中信息,回答下列问题
(1)这个班学生人数有 人;
(2)补全条形统计图,在扇形统计图中其它项目所对的圆心角为 ;
(3)喜欢羽毛球的有3名女同学,其余为男同学,现要从中随机抽取2名同学参加学校的羽毛球队,用列表或树状图求出所抽取的2名同学,恰好2人都是男同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现
如图1,在△OAB和△OCD中,OA=OB,OC=OD,∠AOB=∠COD=40°,连接AC,BD交于点M.填空:
①![]() 的值为 ;
的值为 ;
②∠AMB的度数为 .
(2)类比探究
如图2,在△OAB和△OCD中,∠AOB=∠COD=90°,∠OAB=∠OCD=30°,连接AC交BD的延长线于点M.请判断![]() 的值及∠AMB的度数,并说明理由;
的值及∠AMB的度数,并说明理由;
(3)拓展延伸
在(2)的条件下,将△OCD绕点O在平面内旋转,AC,BD所在直线交于点M,若OD=1,OB=![]() ,请直接写出当点C与点M重合时AC的长.
,请直接写出当点C与点M重合时AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,∠ACB=90°,tanB=![]() ,AB=5,点O为边AB上一动点,以O为圆心,OB为半径的圆交射线BC于点E,以A为圆心,OB为半径的圆交射线AC于点G.
,AB=5,点O为边AB上一动点,以O为圆心,OB为半径的圆交射线BC于点E,以A为圆心,OB为半径的圆交射线AC于点G.
(1)如图1,当点E、G分别在边BC、AC上,且CE=CG时,请判断圆A与圆O的位置关系,并证明你的结论;
(2)当圆O与圆A存在公共弦MN时(如图2),设OB=x,MN=y,求y关于x的函数解析式,并写出定义域;
(3)设圆A与边AB的交点为F,联结OE、EF,当△OEF为以OE为腰的等腰三角形时,求圆O的半径长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,Rt△ABC中,∠A=90°,AB=AC,点D是BC边的中点连接AD,则易证AD=BD=CD,即AD=![]() BC;如图2,若将题中AB=AC这个条件删去,此时AD仍然等于
BC;如图2,若将题中AB=AC这个条件删去,此时AD仍然等于![]() BC.
BC.
理由如下:延长AD到H,使得AH=2AD,连接CH,先证得△ABD≌△CHD,此时若能证得△ABC≌△CHA,
即可证得AH=BC,此时AD=![]() BC,由此可见倍长过中点的线段是我们三角形证明中常用的方法.
BC,由此可见倍长过中点的线段是我们三角形证明中常用的方法.
(1)请你先证明△ABC≌△CHA,并用一句话总结题中的结论;
(2)现将图1中△ABC折叠(如图3),点A与点D重合,折痕为EF,此时不难看出△BDE和△CDF都是等腰直角三角形.BE=DE,CF=DF.由勾股定理可知DE2+DF2=EF2,因此BE2+CF2=EF2,若图2中△ABC也进行这样的折叠(如图4),此时线段BE、CF、EF还有这样的关系式吗?若有,请证明;若没有,请举反例.
(3)在(2)的条件下,将图3中的△DEF绕着点D旋转(如图5),射线DE、DF分别交AB、AC于点E、F,此时(2)中结论还成立吗?请说明理由.图4中的△DEF也这样旋转(如图6),直接写出上面的关系式是否成立.
查看答案和解析>>
科目:初中数学 来源: 题型:
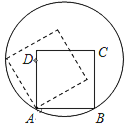
【题目】如图,边长为2的正方形ABCD的顶点A、B在一个半径为2的圆上,顶点C、D在圆内,将正方形ABCD沿圆的内壁作无滑动的滚动.当滚动一周回到原位置时,点C运动的路径长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,以AB的中点O为圆心,OA为半径的圆交AC于点D,E是BC的中点,连接DE,OE.
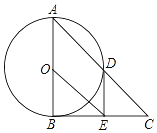
(1)判断DE与⊙O的位置关系,并说明理由;
(2)若cos∠BAD=![]() ,BE=12,求OE的长;
,BE=12,求OE的长;
(3)求证:BC2=2CDOE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景区在同一线路上顺次有三个景点A,B,C,甲、乙两名游客从景点A出发,甲步行到景点C;乙花20分钟时间排队后乘观光车先到景点B,在B处停留一段时间后,再步行到景点C.甲、乙两人离景点A的路程s(米)关于时间t(分钟)的函数图像如图所示.
(1)甲的速度是 米/分钟;
(2)当20≤t ≤30时,求乙离景点A的路程s与t的函数表达式;
(3)乙出发后多长时间与甲在途中相遇?
(4)若当甲到达景点C时,乙与景点C的路程为360米,则乙从景点B步行到景点C的速度是多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com