
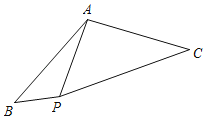
【题目】如图,在△ABC中,∠ABC=90°,以AB的中点O为圆心,OA为半径的圆交AC于点D,E是BC的中点,连接DE,OE.
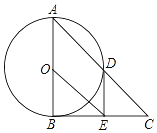
(1)判断DE与⊙O的位置关系,并说明理由;
(2)若cos∠BAD=![]() ,BE=12,求OE的长;
,BE=12,求OE的长;
(3)求证:BC2=2CDOE.
【答案】(1)DE与⊙O相切(2)15(3)证明见解析
【解析】
(1)DE与⊙O相切,连接OD,BD.证明DE⊥OD即可证明DE为⊙O的切线;
(2)由cos∠BAD=![]() 得到sin∠BAC=
得到sin∠BAC=![]() ,又BE=12,BC=24,所以AC=30,又AC=2OE,所以OE=
,又BE=12,BC=24,所以AC=30,又AC=2OE,所以OE=![]() AC=
AC=![]() ×30=15;
×30=15;
(3)OE是△ABC的中位线,所以AC=2OE,证明△ABC∽△BDC,则![]() 即BC2=ACCD=2CDOE.
即BC2=ACCD=2CDOE.
(1)DE与![]() 相切
相切
理由如下:连接 OD,BD.
∵AB为![]() 直径,
直径,
∴∠ADB=90°,
在Rt△BDC中,E为斜边BC的中点,
∴CE=DE=BE= ![]() BC,
BC,
∴∠C=∠CDE,
∵OA=OD,
∴∠A=∠ADO,
∵∠ABC=90°,即∠C+∠A=90°,
∴∠ADO+∠CDE=90°,即∠ODE=90°,
∴DE⊥OD,又OD为圆的半径,
∴DE为![]() 的切线;
的切线;
(2)∵cos∠BAD=![]()
∴sin∠BAC=![]()
又∵BE=12,E是BC的中点,即BC=24,
∴AC=30,
又∵AC=2OE,
∴OE=![]() AC=
AC=![]() ×30=15;
×30=15;
(3)证明:∵E是BC的中点,O点是AB的中点,
∴OE是△ABC的中位线,
∴AC=2OE,
∵∠C=∠C,∠ABC=∠BDC,
∴△ABC∽△BDC,
∴![]()
即BC2=ACCD.
∴BC2=2CDOE


科目:初中数学 来源: 题型:
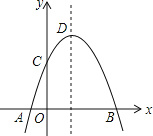
【题目】如图,抛物线y=﹣x2+2x+m+1交x轴于点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D,下列四个命题:
①当x>0时,y>0;
②若a=﹣1,则b=4;
③抛物线上有两点P(x1,y1)和Q(x2,y2),若x1<1<x2,且x1+x2>2,则y1>y2;
④点C关于抛物线对称轴的对称点为E,点G,F分别在x轴和y轴上,当m=2时,四边形EDFG周长的最小值为6![]() .
.
其中真命题的序号是( )
A. ①B. ②C. ③D. ④
查看答案和解析>>
科目:初中数学 来源: 题型:
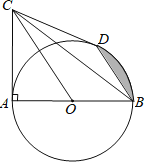
【题目】如图,AB为⊙O的直径,C为⊙O外一点,且∠CAB=90°,BD是⊙O的弦,BD∥CO.
(1)请说明:CD是⊙O的切线:
(2)若AB=4,BC=2![]() .则阴影部分的面积为
.则阴影部分的面积为
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了丰富校园文化生活,促进学生积极参加体育运动,某校准备成立校排球队,现计划购进一批甲、乙两种型号的排球,已知一个甲种型号排球的价格与一个乙种型号排球的价格之和为140元;如果购买6个甲种型号排球和5个乙种型号排球,一共需花费780元.
(1)求每个甲种型号排球和每个乙种型号排球的价格分别是多少元?
(2)学校计划购买甲、乙两种型号的排球共26个,其中甲种型号排球的个数多于乙种型号排球,并且学校购买甲、乙两种型号排球的预算资金不超过1900元,求该学校共有几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,二次函数y=ax2+bx+c(a≠0)的图象如图所示,现给出下列结论:①abc<0;②c+2a>0;③9a﹣3b+c=0;④a﹣b≤am2+bm(m为实数);⑤4ac﹣b2<0.其中正确结论的个数是( )

A. 2B. 3C. 4D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
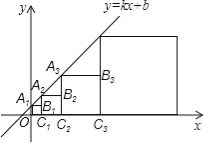
【题目】在直角坐标系中,正方形A1B1C1O1、A2B2C2C1、…、AnBnCnCn﹣1按如图所示的方式放置,其中点A1、A2、A3、…、An均在一次函数y=kx+b的图象上,点C1、C2、C3、…、Cn均在x轴上.若点B1的坐标为(1,1),点B2的坐标为(3,2),则点An的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD,点M是边BA延长线上的动点(不与点A重合),且AM<AB,△CBE由△DAM平移得到.若过点E作EH⊥AC,H为垂足,则有以下结论:①点M位置变化,使得∠DHC=60°时,2BE=DM;②无论点M运动到何处,都有DM=![]() HM;③无论点M运动到何处,∠CHM一定大于135°.其中正确结论的序号为_____.
HM;③无论点M运动到何处,∠CHM一定大于135°.其中正确结论的序号为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段AB绕着点A逆时针方向旋转120°得到线段AC,点B对应点C,在∠BAC的内部有一点P,PA=8,PB=4,PC=4![]() ,则线段AB的长为_____.
,则线段AB的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】同时抛掷两枚硬币,按照正面出现的次数,可以分为“2个正面”、“1个正面”和“没有正面”这3种可能的结果,小红与小明两人共做了6组实验,每组实验都为同时抛掷两枚硬币10次,下表为实验记录的统计表:
结果 | 第一组 | 第二组 | 第三组 | 第四组 | 第五组 | 第六组 |
两个正面 | 3 | 3 | 5 | 1 | 4 | 2 |
一个正面 | 6 | 5 | 5 | 5 | 5 | 7 |
没有正面 | 1 | 2 | 0 | 4 | 1 | 1 |
由上表结果,计算得出现“2个正面”、“1个正面”和“没有正面”这3种结果的频率分别是___________________.当试验组数增加到很大时,请你对这三种结果的可能性的大小作出预测:______________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com