
【题目】△ABC中,∠ACB=90°,tanB=![]() ,AB=5,点O为边AB上一动点,以O为圆心,OB为半径的圆交射线BC于点E,以A为圆心,OB为半径的圆交射线AC于点G.
,AB=5,点O为边AB上一动点,以O为圆心,OB为半径的圆交射线BC于点E,以A为圆心,OB为半径的圆交射线AC于点G.
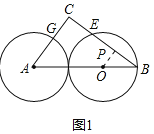
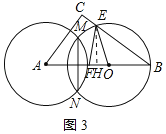
(1)如图1,当点E、G分别在边BC、AC上,且CE=CG时,请判断圆A与圆O的位置关系,并证明你的结论;
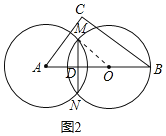
(2)当圆O与圆A存在公共弦MN时(如图2),设OB=x,MN=y,求y关于x的函数解析式,并写出定义域;
(3)设圆A与边AB的交点为F,联结OE、EF,当△OEF为以OE为腰的等腰三角形时,求圆O的半径长.

【答案】(1)圆A与圆O外切,理由见解析;(2)y=![]() (
(![]() <x<5);(3)当△OEF为以OE为腰的等腰三角形时,圆O的半径长为
<x<5);(3)当△OEF为以OE为腰的等腰三角形时,圆O的半径长为![]() 或
或![]() 或5.
或5.
【解析】
(1)由三角函数得出AC=3,BC=4,作OP⊥BE于P,则PB=PE,OP∥AC,得出![]() =
=![]() ,设PB=PE=x,则CG=CE=4﹣2x,得出OB=
,设PB=PE=x,则CG=CE=4﹣2x,得出OB=![]() x,AG=AC﹣CG=2x﹣1,得出方程,得出x=
x,AG=AC﹣CG=2x﹣1,得出方程,得出x=![]() ,OB═
,OB═![]() ,求出OA=AB﹣OB=2OB,即可得出结论;
,求出OA=AB﹣OB=2OB,即可得出结论;
(2)连接OM,由相交两圆的性质得出OA与MN垂直平分,∠ODM=90°,DM=![]() MN=
MN=![]() y,AD=OD=
y,AD=OD=![]() (5﹣x),由勾股定理得出方程,整理即可;
(5﹣x),由勾股定理得出方程,整理即可;
(3)分三种情况:①当圆O与圆A外切,OE=OF时,圆O与圆A外切,圆O的半径长OB=![]() ;
;
②当OE=FE时,圆O与圆A相交,作EH⊥OF于H,则OF=OH=![]() ﹣OB,证明△BEH∽△BAC,得出EH=
﹣OB,证明△BEH∽△BAC,得出EH=![]() ,在Rt△OEH中,由勾股定理得出方程,解方程即可;
,在Rt△OEH中,由勾股定理得出方程,解方程即可;
③当O与A重合时,OE=OF,OE=AB=5;即可得出结论.
(1)圆A与圆O外切,理由如下:
∵∠ACB=90°,tanB=![]() ,AB=5,∴AC=3,BC=4,
,AB=5,∴AC=3,BC=4,
作OP⊥BE于P,如图1所示:
则PB=PE,OP∥AC,
![]() ,
,
设PB=PE=x,则CG=CE=4﹣2x,
![]()
![]()
![]() 解得:x=
解得:x=![]() ,
,
∴OB═![]() ,
,
∴OA=AB﹣OB=5![]() =2OB,
=2OB,
∴圆A与圆O外切;
(2)连接OM,如图2所示:
∵圆O与圆A存在公共弦MN,
∴OA与MN垂直平分,
∴∠ODM=90°,DM=![]()
由勾股定理得:DM2=OM2﹣OD2,即
整理得:y2=3x2+10x﹣25,
∴y=![]() ;
;
(3)分三种情况:
①当圆O与圆A外切,OE=OF时,圆O与圆A外切,圆O的半径长OB=![]() ;
;
②当OE=FE时,圆O与圆A相交,如图3所示:
作EH⊥OF于H,则OF=OH=![]() ﹣OB,
﹣OB,
∵∠B=∠B,∠EHB=90°=∠C,
∴△BEH∽△BAC,
∴![]() ,
,
∴EH=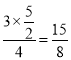 ,
,
在Rt△OEH中,由勾股定理得: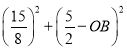 =OE2=OB2,
=OE2=OB2,
解得:OB=![]() ;
;
③当O与A重合时,OE=OF,F与B重合,OE=AB=5;
综上所述,当△OEF为以OE为腰的等腰三角形时,圆O的半径长为![]() 或
或![]() 或5.
或5.


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案科目:初中数学 来源: 题型:
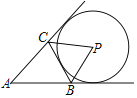
【题目】如图,△ABC中,BC=4,⊙P与△ABC的边或边的延长线相切.若⊙P半径为2,△ABC的面积为5,则△ABC的周长为( )
A.8B.10C.13D.14
查看答案和解析>>
科目:初中数学 来源: 题型:
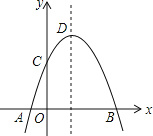
【题目】如图,抛物线y=﹣x2+2x+m+1交x轴于点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D,下列四个命题:
①当x>0时,y>0;
②若a=﹣1,则b=4;
③抛物线上有两点P(x1,y1)和Q(x2,y2),若x1<1<x2,且x1+x2>2,则y1>y2;
④点C关于抛物线对称轴的对称点为E,点G,F分别在x轴和y轴上,当m=2时,四边形EDFG周长的最小值为6![]() .
.
其中真命题的序号是( )
A. ①B. ②C. ③D. ④
查看答案和解析>>
科目:初中数学 来源: 题型:
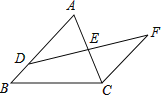
【题目】如图,点D是△ABC的边AB上一点,点E为AC的中点,过点C作CF∥AB交DE延长线于点F.
(1)求证:AD=CF.
(2)连接AF,CD,求证:四边形ADCF为平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=5,BC=12,将矩形绕着点D顺时针旋转,当点C落在对角线BD上的点E处时,点A、B分别落在点G、F处,那么AG:BF:CE=_____.
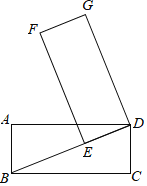
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD⊥AB于H,G为⊙O上一点,连接AG交CD于K,在CD的延长线上取一点E,使EG=EK,EG的延长线交AB的延长线于F.
(1)求证:EF是⊙O的切线;
(2)连接DG,若AC∥EF时.
①求证:△KGD∽△KEG;
②若cosC=![]() ,AK=
,AK=![]() ,求BF的长.
,求BF的长.
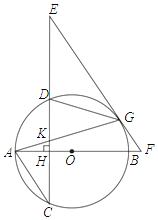
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C为⊙O外一点,且∠CAB=90°,BD是⊙O的弦,BD∥CO.
(1)请说明:CD是⊙O的切线:
(2)若AB=4,BC=2![]() .则阴影部分的面积为
.则阴影部分的面积为
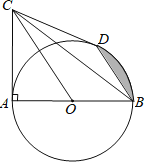
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了丰富校园文化生活,促进学生积极参加体育运动,某校准备成立校排球队,现计划购进一批甲、乙两种型号的排球,已知一个甲种型号排球的价格与一个乙种型号排球的价格之和为140元;如果购买6个甲种型号排球和5个乙种型号排球,一共需花费780元.
(1)求每个甲种型号排球和每个乙种型号排球的价格分别是多少元?
(2)学校计划购买甲、乙两种型号的排球共26个,其中甲种型号排球的个数多于乙种型号排球,并且学校购买甲、乙两种型号排球的预算资金不超过1900元,求该学校共有几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段AB绕着点A逆时针方向旋转120°得到线段AC,点B对应点C,在∠BAC的内部有一点P,PA=8,PB=4,PC=4![]() ,则线段AB的长为_____.
,则线段AB的长为_____.
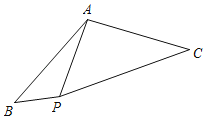
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com