
科目: 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,直线
中,直线![]() 轴,且直线l与抛物线
轴,且直线l与抛物线![]() 和y轴分别交于点A,B,C,点D为抛物线的顶点.若点E的坐标为
和y轴分别交于点A,B,C,点D为抛物线的顶点.若点E的坐标为![]() ,点A的横坐标为1.
,点A的横坐标为1.
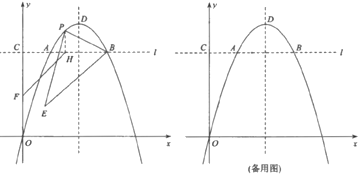
(1)线段AB的长度等于________;
(2)点P为线段AB上方抛物线上的一点,过点P作AB的垂线交AB于点H,点F为y轴上一点,当![]() 的面积最大时,求
的面积最大时,求![]() 的最小值;
的最小值;
(3)在(2)的条件下,删除抛物线![]() 在直线PH左侧部分图象并将右侧部分图象沿直线PH翻折,与抛物线在直线PH右侧部分图象组成新的函数M的图象.现有平行于FH的直线
在直线PH左侧部分图象并将右侧部分图象沿直线PH翻折,与抛物线在直线PH右侧部分图象组成新的函数M的图象.现有平行于FH的直线![]() ,若直线
,若直线![]() 与函数M的图象有且只有2个交点,求t的取值范围(请直接写出t的取值范围,无需解答过程).
与函数M的图象有且只有2个交点,求t的取值范围(请直接写出t的取值范围,无需解答过程).
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,以△ABC的边AB为直径的⊙O与边AC相交于点D,BC是⊙O的切线,E为BC的中点,连接AE、DE.
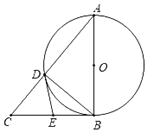
(1)求证:DE是⊙O的切线;
(2)设△CDE的面积为 S1,四边形ABED的面积为 S2.若 S2=5S1,求tan∠BAC的值;
(3)在(2)的条件下,若AE=3![]() ,求⊙O的半径长.
,求⊙O的半径长.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠BAC=30°,AB=4,点M是直角边AC上一动点,连接BM,并将线段BM绕点B逆时针旋转60°得到线段BN,连接CN.则在点M运动过程中,线段CN长度的最大值是_____,最小值是_____.
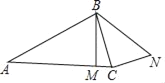
查看答案和解析>>
科目: 来源: 题型:
【题目】已知AD是△ABC的中线P是线段AD上的一点(不与点A、D重合),连接PB、PC,E、F、G、H分别是AB、AC、PB、PC的中点,AD与EF交于点M;
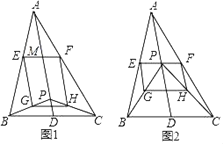
(1)如图1,当AB=AC时,求证:四边形EGHF是矩形;
(2)如图2,当点P与点M重合时,在不添加任何辅助线的条件下,写出所有与△BPE面积相等的三角形(不包括△BPE本身).
查看答案和解析>>
科目: 来源: 题型:
【题目】在矩形ABCD中,AB=6,AD=8,点E是边AD上一点,EM⊥BC交AB于点M,点N在射线MB上,且AE是AM和AN的比例中项.
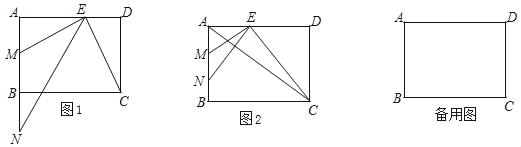
(1)如图1,求证:∠ANE=∠DCE;
(2)如图2,当点N在线段MB之间,联结AC,且AC与NE互相垂直,求MN的长;
(3)连接AC,如果△AEC与以点E、M、N为顶点所组成的三角形相似,求DE的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】计算
(1)(x+y)2-2x(x+y); (2)(a+1)(a-1)-(a-1)2;
(3)先化简,再求值:
(x+2y)(x-2y)-(2x3y-4x2y2)÷2xy,其中x=-3,![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】元旦节前夕,某花店购进康乃馨和玫瑰两种鲜花,销售过程中发现康乃馨比玫瑰销量大,店主决定将玫瑰每枝降价2元促销,降价后80元可购买玫瑰的数量是原来可购买玫瑰数量的1.25倍.
(1)试问:降价后每枝玫瑰的售价是多少元?
(2)根据销售情况,店主用不多于1000元的资金再次购进两种鲜花共180枝,康乃馨进价为6元/枝,玫瑰的进价是5元/枝。试问;至少需要购进多少枝玫瑰?
查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙两人相约周末登花果山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)甲登山上升的速度是每分钟 米,乙在A地时距地面的高度b为 米;
(2)若乙提速后,乙的登山上升速度是甲登山上升速度的3倍,请求出乙登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式;
(3)登山多长时间时,甲、乙两人距地面的高度差为70米?

查看答案和解析>>
科目: 来源: 题型:
【题目】为发展学生的核心素养,培养学生的综合能力,某学校计划开设四门选修课:乐器、舞蹈、绘画、书法,学校采取随机抽样的方法进行问卷调查![]() 每个被调查的学生必须选择而且只能选择其中一门
每个被调查的学生必须选择而且只能选择其中一门![]() 对调查结果进行整理,绘制成如下两幅不完整的统计图
对调查结果进行整理,绘制成如下两幅不完整的统计图![]() 请结合图中所给信息解答下列问题:
请结合图中所给信息解答下列问题:


![]() 本次调查的学生共有______人,在扇形统计图中,m的值是______.
本次调查的学生共有______人,在扇形统计图中,m的值是______.
![]() 分别求出参加调查的学生中选择绘画和书法的人数,并将条形统计图补充完整.
分别求出参加调查的学生中选择绘画和书法的人数,并将条形统计图补充完整.
![]() 该校共有学生2000人,估计该校约有多少人选修乐器课程?
该校共有学生2000人,估计该校约有多少人选修乐器课程?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在Rt△AOB中,∠AOB=90°,OA=3,OB=2,将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE,将线段EF绕点E逆时针旋转90°后得线段ED,分别以O,E为圆心,OA、ED长为半径画弧AF和弧DF,连接AD,则图中阴影部分面积是_____.
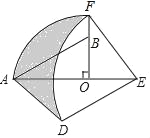
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com