
科目: 来源: 题型:
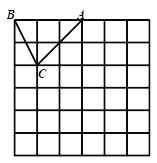
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,△ABC的顶点A、B、C在小正方形的顶点上,将△ABC向下平移4个单位、再向右平移3个单位得到△A1B1C1,然后将△A1B1C1绕点A1顺时针旋转90°得到△A1B2C2.
(1)在网格中画出△A1B1C1和△A1B2C2;
(2)计算线段AC从开始变换到A1 C2的过程中扫过区域的面积(重叠部分不重复计算)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,直角△ABC的三个顶点分别是A(﹣3,1),B(0,3),C(0,1)

(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C1;
(2)分别连结AB1、BA1后,求四边形AB1A1B的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,△ABC的位置如图所示(顶点是网格线的交点)

(1)请画出△ABC向右平移2单位再向下平移3个单位的格点△A1B1C1
(2)画出△ABC绕点O逆时针方向旋转90°得到的△A2B2C2并求出旋转过程中点B到B2所经过的路径长.
查看答案和解析>>
科目: 来源: 题型:
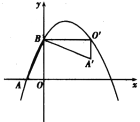
【题目】如图,抛物线y=![]() 与x轴、y轴交于A、B两点,将△OAB绕点B逆时针旋转90°后得到△O′A′B,点O落到点O′的位置,点A落到点A′的位置.
与x轴、y轴交于A、B两点,将△OAB绕点B逆时针旋转90°后得到△O′A′B,点O落到点O′的位置,点A落到点A′的位置.
(1)求点O′和点A′的坐标;
(2)将抛物线沿y轴方向平移后经过点A′,求平移后所得抛物线对应的函数关系式;
(3)设(2)中平移后所得抛物线与y轴的交点为C,与x轴的交点为D,点M在x轴上,点N在平移后所得抛物线上,求出以点C、D、M、N为顶点的四边形是以CD为边的平行四边形时点N的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】在数学兴趣小组的活动中,小明进行数学探究活动,将边长为2的正方形ABCD与边长为2![]() 的正方形AEFG按图①位置放置,AD与AE在同一直线上,AB与AG在同一直线上.
的正方形AEFG按图①位置放置,AD与AE在同一直线上,AB与AG在同一直线上.
⑴小明发现DG⊥BE,请你帮他说明理由.
⑵如图②,小明将正方形ABCD绕点A逆时针旋转,当点B恰好落在线段DG上时,请你帮他求出此时BE的长.

查看答案和解析>>
科目: 来源: 题型:
【题目】高尔夫运动员将一个小球沿与地面成一定角度的方向击出,在不考虑空气阻力的条件下,小球的飞行高度h(m)与它的飞行时间(s)满足二次函数关系,t与h的几组对应值如下表所示:
t(s) | 0 | 0.5 | 1 | 1.5 | 2 | … |
h(m) | 0 | 8.75 | 15 | 18.75 | 20 | … |
(1)求h与t之间的函数关系式(不要求写t的取值范围);
(2)求小球飞行3s时的高度.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,用篱笆靠墙围成矩形花围ABCD,墙可利用的最大长度为15米,一面利用旧墙,其余三面用篱笆围成,篱笆总长为24米.
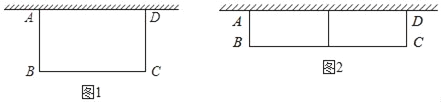
(1)若围成的花圃面积为40米2时,求BC的长;
(2)如图2若计划在花圃中间用一道隔成两个小矩形,且围成的花圃面积为50米2,请你判断能否成功围成花圃,如果能,求BC的长?如果不能,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,由4个全等的正方形组成L形图案,请按下列要求画图:
(1)在图①中添加1个正方形,使它成轴对称图形(不能是中心对称图形);
(2)在图②中添加1个正方形,使它成中心对称图形(不能是轴对称图形);
(3)在图③中改变1个正方形的位置,从而得到一个新图形,使它既成中心对称图形,又成轴对称图形.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,二次函数![]() 的图象与
的图象与![]() 轴正半轴相交,其顶点坐标为
轴正半轴相交,其顶点坐标为![]() ,下列结论:①
,下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④方程
;④方程![]() 有两个相等的实数根,其中正确的结论是________.(只填序号即可).
有两个相等的实数根,其中正确的结论是________.(只填序号即可).
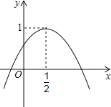
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com