
科目: 来源: 题型:
【题目】(1)如图1,在Rt△ABC 中, ![]() ,D、E是斜边BC上两动点,且∠DAE=45°,将△
,D、E是斜边BC上两动点,且∠DAE=45°,将△![]() 绕点
绕点![]() 逆时针旋转90后,得到△
逆时针旋转90后,得到△![]() ,连接
,连接![]() .
.
(1)试说明:△![]() ≌△
≌△![]() ;
;
(2)当BE=3,CE=9时,求∠BCF的度数和DE的长;
(3)如图2,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,D是斜边BC所在直线上一点,BD=3,BC=8,求DE2的长.

查看答案和解析>>
科目: 来源: 题型:
【题目】某公司研制出新产品,该产品的成本为每件2400元.在试销期间,购买不超过10件时,每件销售价为3000元;购买超过10件时,每多购买一件,所购产品的销售单价均降低5元,但最低销售单价为2600元。请解决下列问题:
(1)直接写出:购买这种产品 ________件时,销售单价恰好为2600元;
(2)设购买这种产品x件(其中x>10,且x为整数),该公司所获利润为y元,求y与x之间的函数表达式;
(3)该公司的销售人员发现:当购买产品的件数超过10件时,会出现随着数量的增多,公司所获利润反而减少这一情况.为使购买数量越多,公司所获利润越大,公司应将最低销售单价调整为多少元?(其它销售条件不变)
查看答案和解析>>
科目: 来源: 题型:
【题目】网购已经成为一种时尚,某网络购物平台“双十一”全天交易额逐年增长,2016年交易额为500亿元,2018年交易额为720亿元。
(1)2016年至2018年“双十一”交易额的年平均增长率是多少?
(2)若保持原来的增长率,试计算2019年该平台“双十一”的交易额将达到多少亿元?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知△ABC的一条边BC的长为5,另两边AB,AC的长分别为关于x的一元二次方程![]() 的两个实数根。
的两个实数根。
(1)求证:无论k为何值,方程总有两个不相等的实数根;
(2)当k=2时,请判断△ABC的形状并说明理由;
(3)k为何值时,△ABC是等腰三角形,并求△ABC的周长。
查看答案和解析>>
科目: 来源: 题型:
【题目】为了改善小区环境,某小区决定要在一块一边靠墙(墙长25m)的空地上修建一个矩形绿化带ABCD,绿化带一边靠墙,其他三边用总长为60米栅栏围住(如图),若设绿化带的BC边为x米,绿化带的面积为y平方米。

(1)求y 关于x 的函数关系式,并写出自变量x 的取值范围:
(2)是否存在绿化带BC的长的某个值,使得绿化带的面积为450平方米?若存在,请求出这个值;若不存在,请说明理由。
查看答案和解析>>
科目: 来源: 题型:
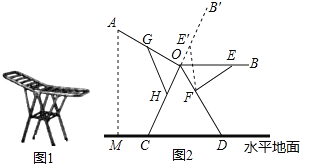
【题目】图1是一种折叠式晾衣架.晾衣时,该晾衣架左右晾衣臂张开后示意图如图2所示,两支脚OC=OD=10分米,展开角∠COD=60°,晾衣臂OA=OB=10分米,晾衣臂支架HG=FE=6分米,且HO=FO=4分米.当∠AOC=90°时,点A离地面的距离AM为_______分米;当OB从水平状态旋转到OB′(在CO延长线上)时,点E绕点F随之旋转至OB′上的点E′处,则B′E′﹣BE为_________分米.
查看答案和解析>>
科目: 来源: 题型:
【题目】如果关于x的一元二次方程![]() 有两个实数根,且其中一个根为另一个根的2倍,则称这样的方程为“倍根方程”.以下关于倍根方程的说法,正确的是________.(写出所有正确说法的序号).
有两个实数根,且其中一个根为另一个根的2倍,则称这样的方程为“倍根方程”.以下关于倍根方程的说法,正确的是________.(写出所有正确说法的序号).
①方程![]() 是倍根方程;
是倍根方程;
②若![]() 是倍根方程,则
是倍根方程,则![]() ;
;
③若点![]() 在反比例函数
在反比例函数![]() 的图像上,则关于
的图像上,则关于![]() 的方程
的方程![]() 是倍根方程;
是倍根方程;
④若方程![]() 是倍根方程,且相异两点
是倍根方程,且相异两点![]() ,
, ![]() 都在抛物线
都在抛物线![]() 上,则方程
上,则方程![]() 的一个根为
的一个根为![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象经过点A(﹣1,0)、点B(3,0)、点C(4,y1),若点D(x2,y2)是抛物线上任意一点,有下列结论:
①二次函数y=ax2+bx+c的最小值为﹣4a;
②若﹣1≤x2≤4,则0≤y2≤5a;
③若y2>y1,则x2>4;
④一元二次方程cx2+bx+a=0的两个根为﹣1和![]()
其中正确结论的个数是( )
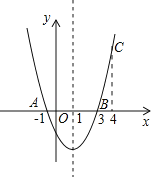
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目: 来源: 题型:
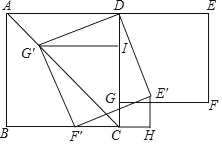
【题目】如图,在正方形ABCD和正方形DEFG中,点G在CD上,DE=2,将正方形DEFG绕点D顺时针旋转60°,得到正方形DE′F′G′,此时点G′在AC上,连接CE′,则CE′+CG′=( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com