
科目: 来源: 题型:
【题目】如图,在矩形ABCD中,E、F分别是边AB、CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于O点,且BE=BF,∠BEF=2∠BAC。

(1)求证:OE=OF;
(2)若BC=![]() ,求AB的长。
,求AB的长。
查看答案和解析>>
科目: 来源: 题型:
【题目】已知关于x的方程![]()
(1)求证:不论k取什么实数值,这个方程总有实数根;
(2)若等腰三角形ABC的一边长为![]() ,另两边的长b、c恰好是这个方程的两个根,求△ABC的周长.
,另两边的长b、c恰好是这个方程的两个根,求△ABC的周长.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,正方形ABCD的边CD与Rt△EFG的直角边EF重合,将正方形ABCD以1cm/s的速度沿FE方向移动,在移动过程中,边CD始终与边EF重合(移动开始时点C与点F重合).连接AE,过点C作AE的平行线交直线EG于点H,连接HD.已知正方形ABCD的边长为1cm,EF=4cm,设正方形移动时间为x(s),线段EH的长为y(cm),其中0≤x≤2.5.
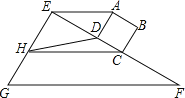
(1)当x=2时,AE的长为 ;
(2)试求出y关于x的函数关系式,并求出△EHD与△ADE的面积之差;
(3)当正方形ABCD移动时间x= 时,线段HD所在直线经过点B.
查看答案和解析>>
科目: 来源: 题型:
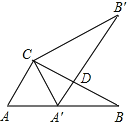
【题目】如图,Rt△ABC中,∠ACB=90°,∠B=30°,AC=2,将△ABC绕点C逆时针旋转至△A′B′C,使得点A′恰好落在AB上,A′B′与BC交于点D,则△A′CD的面积为( )
A.![]() B.5
B.5![]() C.5D.2
C.5D.2![]()
查看答案和解析>>
科目: 来源: 题型:
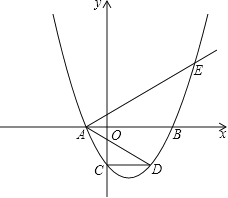
【题目】如图,二次函数![]() (其中a,m是常数,且a>0,m>0)的图象与x轴分别交于点A,B(点A位于点B的左侧),与y轴交于点C(0,-3),点D在二次函数的图象上,CD∥AB,连接AD.过点A作射线AE交二次函数的图象于点E,AB平分∠DAE.
(其中a,m是常数,且a>0,m>0)的图象与x轴分别交于点A,B(点A位于点B的左侧),与y轴交于点C(0,-3),点D在二次函数的图象上,CD∥AB,连接AD.过点A作射线AE交二次函数的图象于点E,AB平分∠DAE.
(1)用含m的代数式表示a;
(2))求证:![]() 为定值;
为定值;
(3)设该二次函数图象的顶点为F.探索:在x轴的负半轴上是否存在点G,连接CF,以线段GF、AD、AE的长度为三边长的三角形是直角三角形?如果存在,只要找出一个满足要求的点G即可,并用含m的代数式表示该点的横坐标;如果不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,第一象限内半径为2的⊙C与y轴相切于点A,作直径AD,过点D作⊙C的切线l交x轴于点B,P为直线l上一动点,已知直线PA的解析式为:y=kx+3.
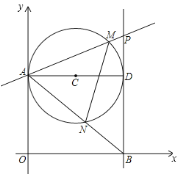
(1)设点P的纵坐标为p,写出p随k变化的函数关系式.
(2)设⊙C与PA交于点M,与AB交于点N,则不论动点P处于直线l上(除点B以外)的什么位置时,都有△AMN∽△ABP.请你对于点P处于图中位置时的两三角形相似给予证明;
(3)是否存在使△AMN的面积等于![]() 的k值?若存在,请求出符合的k值;若不存在,请说明理由.
的k值?若存在,请求出符合的k值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,一艘渔船位于码头M的南偏东45°方向,距离码头120海里的B处,渔船从B处沿正北方向航行一段距离后,到达位于码头北偏东60°方向的A处.
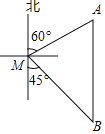
(1)求渔船从B到A的航行过程中与码头M之间的最小距离.
(2)若渔船以20海里/小时的速度从A沿AM方向行驶,求渔船从A到达码头M的航行时间.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在由边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点)和点A1.
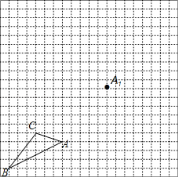
(1)将△ABC绕点A顺时针旋转90°,画出相应的△AB1C1;
(2)将△AB1C1沿射线AA1平移到△A1B2C2处,画出△A1B2C2;
(3)点C在两次变换过程中所经过的路径长为 .
查看答案和解析>>
科目: 来源: 题型:
【题目】温州市政府计划投资百亿元开发瓯江口新区,打造出一个“东方时尚岛、海上新温州”.为了解温州市民对瓯江口新区的关注情况,某学校数学兴趣小组随机采访部分温州市民,对采访情况制作了统计图表的一部分如下:
关注情况 | 频数 | 频率 |
A.高度关注 | m | 0.1 |
B.一般关注 | 100 | 0.5 |
C.不关注 | 30 | n |
D.不知道 | 50 | 0.25 |
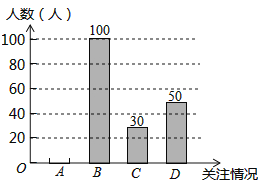
(1)根据上述统计表可得此次采访的人数为 人;m= ,n= ;
(2)根据以上信息补全条形统计图;
(3)根据上述采访结果,估计25000名温州市民中高度关注瓯江口新区的市民约 人.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知在圆O中,AB是直径,点E和点D是圆O上的点,且∠EAB=45°,延长AE和BD相交于点C,连接BE和AD交于点F,BD=12,CD=8,则直径AB的长是_____.
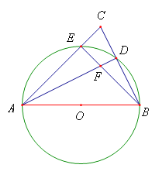
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com