
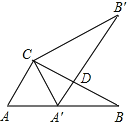
【题目】如图,Rt△ABC中,∠ACB=90°,∠B=30°,AC=2,将△ABC绕点C逆时针旋转至△A′B′C,使得点A′恰好落在AB上,A′B′与BC交于点D,则△A′CD的面积为( )
A.![]() B.5
B.5![]() C.5D.2
C.5D.2![]()
【答案】A
【解析】
根据旋转的性质得CA=CA′=2,∠CA′B′=∠A=60°,则△CAA′为等边三角形,所以∠ACA′=60°,则可计算出∠BCA′=30°,∠A′DC=90°,然后在Rt△A′DC中利用含30度的直角三角形三边的关系得A′D=![]() CA′=1,CD=
CA′=1,CD=![]() A′D=
A′D=![]() ,再利用三角形面积公式求解.
,再利用三角形面积公式求解.
在Rt△ACB=90°,∵∠B=30°,
∴∠A=60°,
∵△ABC绕点C逆时针旋转至△A′B′C,使得点A′恰好落在AB上,
∴CA=CA′=2,∠CA′B′=∠A=60°,
∴△CAA′为等边三角形,
∴∠ACA′=60°,
∴∠BCA′=30°,
∴∠A′DC=90°,
在Rt△A′DC中,∵∠A′CD=30°,
∴A′D=![]() CA′=1,CD=
CA′=1,CD=![]() A′D=
A′D=![]() ,
,
∴△A′CD的面积=![]() ×1×
×1×![]() =
=![]() .
.
故选:A.


科目:初中数学 来源: 题型:
【题目】(8分)如图,已知O是坐标原点,B、C两点的坐标分别为(3,-1)、(2,1)。

(1)以O点为位似中心在y轴的左侧将△OBC放大到两倍画出图形。
(2)写出B、C两点的对应点B、C的坐标;
(3)如果△OBC内部一点M的坐标为(x,y),写出M的对应点M的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着粤港澳大湾区建设的加速推进,广东省正加速布局以5G等为代表的战略性新兴产业,据统计,目前广东5G基站的数量约1.5万座,计划到2020年底,全省5G基站数是目前的4倍,到2022年底,全省5G基站数量将达到17.34万座。
(1)计划到2020年底,全省5G基站的数量是多少万座?;
(2)按照计划,求2020年底到2022年底,全省5G基站数量的年平均增长率。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四张完全相同的卡片上,分别画有圆、正方形、等边三角形和线段,现从中随机抽取两张,卡片上画的恰好都是中心对称图形的概率为( )
A.1B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】温州市政府计划投资百亿元开发瓯江口新区,打造出一个“东方时尚岛、海上新温州”.为了解温州市民对瓯江口新区的关注情况,某学校数学兴趣小组随机采访部分温州市民,对采访情况制作了统计图表的一部分如下:
关注情况 | 频数 | 频率 |
A.高度关注 | m | 0.1 |
B.一般关注 | 100 | 0.5 |
C.不关注 | 30 | n |
D.不知道 | 50 | 0.25 |
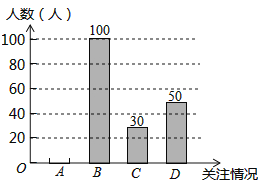
(1)根据上述统计表可得此次采访的人数为 人;m= ,n= ;
(2)根据以上信息补全条形统计图;
(3)根据上述采访结果,估计25000名温州市民中高度关注瓯江口新区的市民约 人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某中学准备在校园里利用围墙的一段,再砌三面墙,围成一个矩形花园ABCD(围墙MN最长可利用25m),现在已备足可以砌50m长的墙的材料,试设计一种砌法,使矩形花园的面积为300m2.
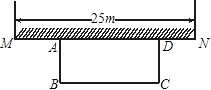
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场举办抽奖活动,规则如下:在不透明的袋子中有2个红球和2个黑球,这些球除颜色外都相同,顾客每次摸出一个球,若摸到红球,则获得1份奖品,若摸到黑球,则没有奖品。
(1)如果小芳只有一次摸球机会,那么小芳获得奖品的概率为 ;
(2)如果小芳有两次摸球机会(摸出后不放回),求小芳获得2份奖品的概率。(请用“画树状图”或“列表”等方法写出分析过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
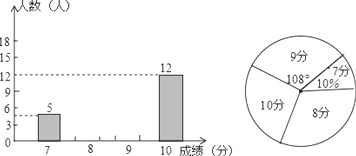
【题目】为了了解外国语中学2016级学生的跳绳成绩,罗老师随机调查了该年级体育模拟考试中部分同学的跳绳成绩,并绘制成了如图所示的条形统计图和扇形统计图.请你根据图中提供的信息完成下列各题:
(1)被调查同学跳绳成绩的中位数是 ,并补全上面的条形统计图;
(2)如果我校初三年级共有学生1200人,估计跳绳成绩能得9分的学生约有 人;
(3)从初三学生中随机抽取一人,求所抽同学本次跳绳成绩恰好为8分得概率。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,M为BC上一点,ME⊥AM,ME交AD的延长线于点E.
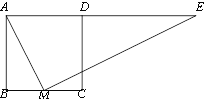
(1)求证:△ABM ∽△EMA;
(2)若AB=2,BM=1,求DE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com