
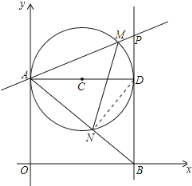
°æƒø°ø»ÁÕº£¨µ⁄“ªœÛœÞƒ⁄∞Îæ∂Œ™2µƒ°—C”Îy÷·œý«–”⁄µ„A£¨◊˜÷±æ∂AD£¨π˝µ„D◊˜°—Cµƒ«–œþlΩªx÷·”⁄µ„B£¨PŒ™÷±œþl…œ“ª∂ص„£¨“—÷™÷±œþPAµƒΩ‚Œˆ ΩŒ™£∫y£Ωkx+3£Æ
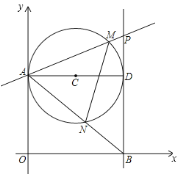
£®1£©…˵„Pµƒ◊ð◊¯±ÍŒ™p£¨–¥≥ˆpÀÊk±‰ªØµƒ∫Ø ˝πÿœµ Ω£Æ
£®2£©…Ë°—C”ÎPAΩª”⁄µ„M£¨”ÎABΩª”⁄µ„N£¨‘Ú≤ª¬€∂ص„P¥¶”⁄÷±œþl…œ£®≥˝µ„B“‘Õ‚£©µƒ ≤√¥Œª÷√ ±£¨∂º”–°˜AMN°◊°˜ABP£Æ«Îƒ„∂‘”⁄µ„P¥¶”⁄Õº÷–Œª÷√ ±µƒ¡Ω»˝Ω«–ŒœýÀ∆∏¯”Ë÷§√˜£ª
£®3£© «∑ҥʑ⁄ π°˜AMNµƒ√ʪ˝µ»”⁄![]() µƒk÷µ£ø»Ù¥Ê‘⁄£¨«Î«Û≥ˆ∑˚∫œµƒk÷µ£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
µƒk÷µ£ø»Ù¥Ê‘⁄£¨«Î«Û≥ˆ∑˚∫œµƒk÷µ£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
°æ¥∞∏°ø(1) p£Ω4k+3£ª(2)º˚Ω‚Œˆ;(3) ¥Ê‘⁄£¨k£Ω2°¿![]() ªÚk£Ω©Å2 ±£¨°˜AMNµƒ√ʪ˝µ»”⁄
ªÚk£Ω©Å2 ±£¨°˜AMNµƒ√ʪ˝µ»”⁄![]() ,¿Ì”…º˚Ω‚Œˆ
,¿Ì”…º˚Ω‚Œˆ
°æΩ‚Œˆ°ø
£®1£©”…«–œþµƒ–‘÷ ÷™°œAOB£Ω°œOAD£Ω°œADB£Ω90°„£¨À˘“‘ø…“‘≈–∂®Àƒ±þ–ŒOADB «æÿ–Œ£ª∏˘æð°—Oµƒ∞Îæ∂ «2«Ûµ√÷±æ∂AD£Ω4£¨¥”∂¯«Ûµ√µ„Pµƒ◊¯±Í£¨Ω´∆‰¥˙»Î÷±œþ∑Ω≥Ãy£Ωkx£´3º¥ø…÷™p±‰ªØµƒ∫Ø ˝πÿœµ Ω£ª
£®2£©¡¨Ω”DN£Æ°þ÷±æ∂À˘∂‘µƒ‘≤÷ÐΩ« «÷±Ω«£¨°ý°œAND£Ω90°„£¨∏˘æðÕº æ“◊÷§°œAND£Ω°œABD£ª»ª∫Û∏˘æðÕ¨ª°À˘∂‘µƒ‘≤÷ÐΩ«œýµ»Õ∆÷™°œADN£Ω°œAMN£¨‘Ÿ”…µ»¡ø¥˙ªªø…÷™°œABD£Ω°œAMN£ª◊Ó∫Û¿˚”√œýÀ∆»˝Ω«–Œµƒ≈–∂®∂®¿ÌAA÷§√˜°˜AMN°◊°˜ABP£ª
£®3£©¥Ê‘⁄£Æ∞—x£Ω0¥˙»Îy£Ωkx£´3µ√y£Ω3£¨º¥OA£ΩBD£Ω3£¨»ª∫Û”…π¥π…∂®¿Ì«Ûµ√AB£Ω5£ª”÷”…œýÀ∆»˝Ω«–ŒµƒœýÀ∆±»Õ∆÷™œýÀ∆»˝Ω«–Œµƒ√ʪ˝±»£Æ∑÷¡Ω÷÷«ÈøˆΩ¯––Ã÷¬€£∫¢Ÿµ±µ„P‘⁄Bµ„…œ∑Ω ±£¨”…œýÀ∆»˝Ω«–Œµƒ√ʪ˝±»µ√µΩk24k2£Ω0£¨Ω‚πÿ”⁄kµƒ“ª‘™∂˛¥Œ∑Ω≥㪢⁄µ±µ„P‘⁄Bµ„œ¬∑Ω ±£¨”…œýÀ∆»˝Ω«–Œµƒ√ʪ˝±»µ√µΩk2£´1£Ω£®4k£´3£©£¨Ω‚πÿ”⁄kµƒ“ª‘™∂˛¥Œ∑Ω≥ãÆ
£®1£©°þy÷·∫Õ÷±œþl∂º «°—Cµƒ«–œþ£¨°ýOA°ÕAD£¨BD°ÕAD£ª”÷°þOA°ÕOB£¨
°ý°œAOB£Ω°œOAD£Ω°œADB£Ω90°„£¨°ýÀƒ±þ–ŒOADB «æÿ–Œ£ª°þ°—Cµƒ∞Îæ∂Œ™2£¨°ýAD£ΩOB£Ω4£ª
°þµ„P‘⁄÷±œþl…œ£¨°ýµ„Pµƒ◊¯±ÍŒ™£®4£¨p£©£ª”÷°þµ„P“≤‘⁄÷±œþAP…œ£¨°ýp£Ω4k+3£ª
£®2£©¡¨Ω”DN£Æ°þAD «°—Cµƒ÷±æ∂£¨°ý°œAND£Ω90°„£¨
°þ°œADN£Ω90°„©Å°œDAN£¨°œABD£Ω90°„©Å°œDAN£¨°ý°œADN£Ω°œABD£¨”÷°þ°œADN£Ω°œAMN£¨
°ý°œABD£Ω°œAMN£¨°þ°œMAN£Ω°œBAP£¨°ý°˜AMN°◊°˜ABP
£®3£©¥Ê‘⁄£Æ¿Ì”…£∫∞—x£Ω0¥˙»Îy£Ωkx+3µ√£∫y£Ω3£¨º¥OA£ΩBD£Ω3£¨AB£Ω![]() £¨
£¨
°þS°˜ABD£Ω![]() ABDN£Ω
ABDN£Ω![]() ADDB°ýDN£Ω
ADDB°ýDN£Ω![]() £Ω
£Ω![]() £¨°ýAN2£ΩAD2©ÅDN2£Ω
£¨°ýAN2£ΩAD2©ÅDN2£Ω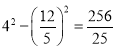 £¨
£¨
°þ°˜AMN°◊°˜ABP£¨°ý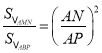 £¨º¥
£¨º¥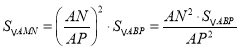
µ±µ„P‘⁄Bµ„…œ∑Ω ±£¨°þAP2£ΩAD2+PD2£ΩAD2+£®PB©ÅBD£©2£Ω42+£®4k+3©Å3£©2£Ω16£®k2+1£©£¨
ªÚAP2£ΩAD2+PD2£ΩAD2+£®BD©ÅPB£©2£Ω42+£®3©Å4k©Å3£©2£Ω16£®k2+1£©£¨
S°˜ABP£Ω![]() PBAD£Ω
PBAD£Ω![]() £®4k+3£©°¡4£Ω2£®4k+3£©£¨
£®4k+3£©°¡4£Ω2£®4k+3£©£¨
°ý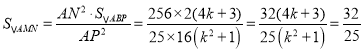 £¨
£¨
’˚¿Ìµ√£∫k2©Å4k©Å2£Ω0£¨Ω‚µ√k1£Ω2+![]() £¨k2£Ω2©Å
£¨k2£Ω2©Å![]()
µ±µ„P‘⁄Bµ„œ¬∑Ω ±£¨
°þAP2£ΩAD2+PD2£Ω42+£®3©Å4k©Å3£©2£Ω16£®k2+1£©£¨S°˜ABP£Ω![]() PBAD£Ω
PBAD£Ω![]() [©Å£®4k+3£©]°¡4£Ω©Å2£®4k+3£©
[©Å£®4k+3£©]°¡4£Ω©Å2£®4k+3£©
°ý
ªØºÚµ√£∫k2+1£Ω©Å£®4k+3£©£¨Ω‚µ√£∫k£Ω©Å2£¨
◊€∫œ“‘…œÀ˘µ√£¨µ±k£Ω2°¿![]() ªÚk£Ω©Å2 ±£¨°˜AMNµƒ√ʪ˝µ»”⁄
ªÚk£Ω©Å2 ±£¨°˜AMNµƒ√ʪ˝µ»”⁄![]()


 √˚–£øŒÃ√œµ¡–¥∞∏
√˚–£øŒÃ√œµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨∆Ω––Àƒ±þ–ŒABCD÷–£¨π˝µ„Bµƒ÷±œþ”Î∂‘Ω«œþAC°¢±þAD∑÷±Ωª”⁄µ„E∫ÕF£Æπ˝µ„E◊˜EG°ŒBC£¨ΩªAB”⁄G£¨‘ÚÕº÷–œýÀ∆»˝Ω«–Œ”–£® £©
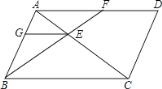
A. 7∂‘ B. 6∂‘ C. 5∂‘ D. 4∂‘
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
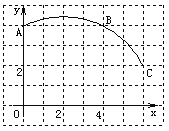
°æƒø°ø∂˛¥Œ∫Ø ˝y=ax2+bx+c£®a°Ÿ0£©µƒÕºœÛ»ÁÕºÀ˘ 棨∏˘æðÕºœÛΩ‚¥œ¬¡–Œ £∫
£®1£©–¥≥ˆ∑Ω≥Ãax2+bx+c=0µƒ¡Ω∏ˆ∏˘£ª
£®2£©–¥≥ˆ≤ªµ» Ωax2+bx+c<0µƒΩ‚ºØ£ª
£®3£©»Ù∑Ω≥Ãax2+bx+c+k=0”–¡Ω∏ˆ≤ªœýµ»µƒ µ ˝∏˘£¨«Ûkµƒ»°÷µ∑∂Œß£Æ
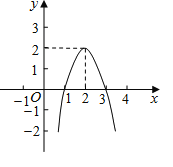
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
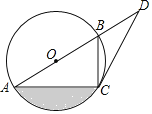
°æƒø°ø»ÁÕº£¨“—÷™AB «°—O…œµƒµ„£¨C «°—O…œµƒµ„£¨µ„D‘⁄ABµƒ—”≥§œþ…œ£¨°œBCD=°œBAC£Æ
£®1£©«Û÷§£∫CD «°—Oµƒ«–œþ£ª
£®2£©»Ù°œD=30°„£¨BD=2£¨«ÛÕº÷–“ı”∞≤ø∑÷µƒ√ʪ˝£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨°˜ABC «±þ≥§Œ™4µƒ’˝»˝Ω«–Œ£¨“‘AB±þ◊˜’˝∑Ω–ŒABDE£¨µ„P∫Õµ„Q∑÷± «œþ∂ŒAC∫Õœþ∂ŒBC…œµƒ÷–µ„£¨¡¨Ω”AQ∫ÕBPœýΩª”⁄µ„M£¨‘Úµ„MµΩDEµƒæý¿Î «_____£Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄æÿ–ŒABCD÷–£¨E°¢F∑÷± «±þAB°¢CD…œµƒµ„£¨AE=CF£¨¡¨Ω”EF£¨BF£¨EF”Î∂‘Ω«œþACΩª”⁄Oµ„£¨«“BE=BF£¨°œBEF=2°œBAC°£

£®1£©«Û÷§£∫OE=OF£ª
£®2£©»ÙBC=![]() £¨«ÛABµƒ≥§°£
£¨«ÛABµƒ≥§°£
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
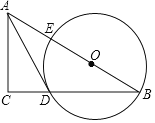
°æƒø°ø»ÁÕº£¨‘⁄Rt°˜ABC÷–£¨µ„O‘⁄–±±þAB…œ£¨“‘OŒ™‘≤–ƒ£¨OBŒ™∞Îæ∂◊˜‘≤£¨∑÷±”ÎBC£¨ABœýΩª”⁄µ„D£¨E£¨¡¨Ω·AD£Æ“—÷™°œCAD=°œB,
£®1£©«Û÷§£∫AD «°—Oµƒ«–œþ£Æ
£®2£©»ÙBC=8£¨tanB=![]() £¨«Û°—O µƒ∞Îæ∂£Æ
£¨«Û°—O µƒ∞Îæ∂£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄’˝∑Ω–ŒÕ¯∏ÒÕº÷–Ω®¡¢“ª÷±Ω«◊¯±Íœµ£¨“ªÃı‘≤ª°æ≠π˝Õ¯∏Òµ„A°¢B°¢C£¨«Îªÿ¥£∫
£®1£©∏√‘≤ª°À˘‘⁄‘≤–ƒDµ„µƒ◊¯±ÍŒ™ £ª
£®2£©…»–ŒDACµƒ‘≤–ƒΩ«∂» ˝Œ™ £ª
£®3£©»Ù…»–ŒDAC «ƒ≥“ª∏ˆ‘≤◊∂µƒ≤ý√Ê’πø™Õº£¨«Û∏√‘≤◊∂µƒ∏þ£Æ£®±£¡Ù∏˘∫≈£©
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
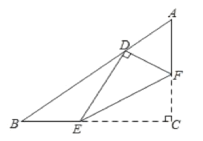
°æƒø°ø»ÁÕº,‘⁄Rt°˜ABC÷–,°œC=90°„£¨AC=3£¨BC=4£¨µ„E£¨F∑÷±‘⁄±þBC£¨AC…œ£¨—ÿEFÀ˘‘⁄µƒ÷±œþ’€µ˛°œC£¨ πµ„Cµƒ∂‘”¶µ„D«°∫√¬‰‘⁄±þAB…œ£¨»Ù°˜EFC∫Õ°˜ABCœýÀ∆£¨‘ÚADµƒ≥§Œ™___.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com