
科目: 来源: 题型:
【题目】已知在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为射线
为射线![]() 上一点(与点
上一点(与点![]() 不重合),过点
不重合),过点![]() 作
作![]() 于点
于点![]() ,且
,且![]() (点
(点![]() 与点
与点![]() 在射线
在射线![]() 同侧),连接
同侧),连接![]() ,
,![]() .
.
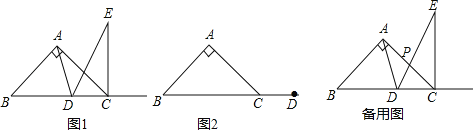
(1)如图1,当点![]() 在线段
在线段![]() 上时,请直接写出
上时,请直接写出![]() 的度数.
的度数.
(2)当点![]() 在线段
在线段![]() 的延长线上时,依题意在图2中补全图形并判断(1)中结论是否成立?若成立,请证明;若不成立,请说明理由.
的延长线上时,依题意在图2中补全图形并判断(1)中结论是否成立?若成立,请证明;若不成立,请说明理由.
(3)在(1)的条件下,![]() 与
与![]() 相交于点
相交于点![]() ,若
,若![]() ,直接写出
,直接写出![]() 的最大值.
的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() (点
(点![]() 在点
在点![]() 的左侧),对称轴与
的左侧),对称轴与![]() 轴交于点(3,0),且
轴交于点(3,0),且![]() .
.
(1)求抛物线![]() 的表达式及顶点坐标;
的表达式及顶点坐标;
(2)将抛物线![]() 平移,得到的新抛物线
平移,得到的新抛物线![]() 的顶点为(0,﹣1),抛物线
的顶点为(0,﹣1),抛物线![]() 的对称轴与两条抛物线
的对称轴与两条抛物线![]() ,
,![]() 围成的封闭图形为
围成的封闭图形为![]() .直线
.直线![]() 经过点
经过点![]() .若直线
.若直线![]() 与图形
与图形![]() 有公共点,求
有公共点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知![]() 是
是![]() 的函数,如表是
的函数,如表是![]() 与
与![]() 的几组对应值.
的几组对应值.
| … | ﹣5 | ﹣4 | ﹣3 | ﹣2 | 0 | 1 | 2 | 3 | 4 | 5 | … |
| … | 1.969 | 1.938 | 1.875 | 1.75 | 1 | 0 | ﹣2 | ﹣1.5 | 0 | 2.5 | … |
小明根据学习函数的经验,利用上述表格所反映出的![]() 与
与![]() 之间的变化规律,对该函数的图象与性质进行了探究.
之间的变化规律,对该函数的图象与性质进行了探究.
下面是小明的探究过程,请补充完整:

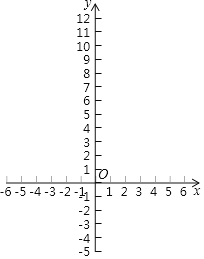
(1)如图,在平面直角坐标系![]() 中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
(2)根据画出的函数图象,写出:
①![]() 对应的函数值
对应的函数值![]() 约为 ;
约为 ;
②该函数的一条性质: .
查看答案和解析>>
科目: 来源: 题型:
【题目】绿色出行是对环境影响最小的出行方式,“共享单车”已成为北京的一道靓丽的风景线.某社会实践活动小
组为了了解“共享单车”的使用情况,对本校教师在3月6日至3月10日使用单车的情况进行了问卷调查,
以下是根据调查结果绘制的统计图的一部分:
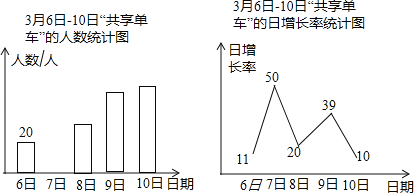
请根据以上信息解答下列问题:
(1)3月7日使用“共享单车”的教师人数为人,并请补全条形统计图;
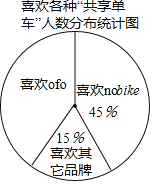
(2)不同品牌的“共享单车”各具特色,社会实践活动小组针对有过使用“共享单车”经历的教师做了进一步调查,每位教师都按要求选择了一种自己喜欢的“共享单车”,统计结果如图,其中喜欢![]() 的教师有36人,求喜欢
的教师有36人,求喜欢![]() 的教师的人数.
的教师的人数.
查看答案和解析>>
科目: 来源: 题型:
【题目】某林业部门统计某种树苗在本地区一定条件下的移植成活率,结果如表:
移植的棵数 | 300 | 700 | 1000 | 5000 | 15000 |
成活的棵数 | 280 | 622 | 912 | 4475 | 13545 |
成活的频率 | 0.933 | 0.889 | 0.912 | 0.895 | 0.903 |
根据表中的数据,估计这种树苗移植成活的概率为_____(精确到0.1);如果该地区计划成活4.5万棵幼树,那么需要移植这种幼树大约_____万棵.
查看答案和解析>>
科目: 来源: 题型:
【题目】下面是“已知底边及底边上的高线作等腰三角形”的尺规作图过程.
已知:线段![]() .求作:等腰
.求作:等腰![]() ,使
,使![]() ,
,![]() 边上的高为
边上的高为![]() .作法:如图,(1)作线段
.作法:如图,(1)作线段![]() ;(2)作线段
;(2)作线段![]() 的垂直平分线
的垂直平分线![]() 交
交![]() 于点
于点![]() ;(3)在射线
;(3)在射线![]() 上顺次截取线段
上顺次截取线段![]() ,连接
,连接![]() .所以
.所以![]() 即为所求作的等腰三角形.
即为所求作的等腰三角形.
请回答:得到![]() 是等腰三角形的依据是:
是等腰三角形的依据是:
①_____:
②_____.
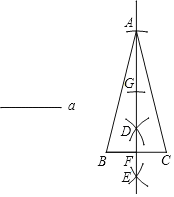
查看答案和解析>>
科目: 来源: 题型:
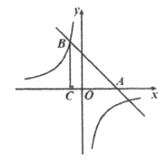
【题目】如图,在平面直角坐标系xOy中,直线![]() 与x轴交于点A,与双曲线
与x轴交于点A,与双曲线![]() 的一个交点为B(-1,4).
的一个交点为B(-1,4).
(1)求直线与双曲线的表达式;
(2)过点B作BC⊥x轴于点C,若点P在双曲线![]() 上,且△PAC的面积为4,求点P的坐标.
上,且△PAC的面积为4,求点P的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四边形ABCD是矩形,点E在AD边上,点F在AD的延长线上,且BE=CF.
(1)求证:四边形EBCF是平行四边形.
(2)若∠BEC=90°,∠ABE=30°,AB=![]() ,求ED的长.
,求ED的长.

查看答案和解析>>
科目: 来源: 题型:
【题目】我们给出如下定义:两个图形![]() 和
和![]() ,在
,在![]() 上的任意一点
上的任意一点![]() 引出两条垂直的射线与
引出两条垂直的射线与![]() 相交于点
相交于点![]() 、
、![]() ,如果
,如果![]() ,我们就称
,我们就称![]() 、
、![]() 为点
为点![]() 的垂等点,
的垂等点,![]() 、
、![]() 为点
为点![]() 的垂等线段,点
的垂等线段,点![]() 为垂等射点.
为垂等射点.
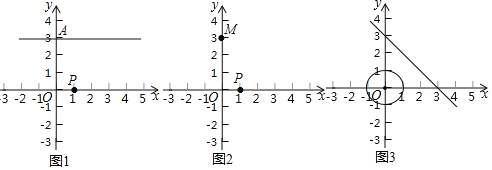
(1)如图1,在平面直角坐标系![]() 中,点
中,点![]() 为
为![]() 轴上的垂等射点,过
轴上的垂等射点,过![]() 作
作![]() 轴的平行线
轴的平行线![]() ,则直线
,则直线![]() 上的
上的![]() 为点
为点![]() 的垂等点的是_______;
的垂等点的是_______;
(2)如果一次函数图象过![]() ,点
,点![]() 为垂等射点
为垂等射点![]() 的一个垂等点且另一个垂等点
的一个垂等点且另一个垂等点![]() 也在此一次函数图象上,在图2中画出示意图并写出一次函数表达式;
也在此一次函数图象上,在图2中画出示意图并写出一次函数表达式;
(3)如图3,以点![]() 为圆心,1为半径作
为圆心,1为半径作![]() ,垂等射点
,垂等射点![]() 在
在![]() 上,垂等点在经过(3,0),(0,3)的直线上,如果关于点
上,垂等点在经过(3,0),(0,3)的直线上,如果关于点![]() 的垂等线段始终存在,求垂等线段
的垂等线段始终存在,求垂等线段![]() 长的取值范围(画出图形直接写出答案即可).
长的取值范围(画出图形直接写出答案即可).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com